About

临时赶工出来的一个数理方程的 pre.

/_img/meme/no-cas-all-human-integration.jpg

~~(明明没时间还要做 meme 的屑)~~

([2023-06-15] Note: 时间浪费了太多了, 后面一段没时间做得更加细致了, 先摆了, 以后再补 (用 [] 表示这部分是我摆了). )

CAS (Computer Algebra System)

所谓的 CAS (Computer Algebra System, 计算机代数系统), 一个非常狭隘的介绍就是可以进行符号运算 (微积分之类的). 主要使用的还是 Mathematica, 不过最近渐渐开始尝试使用其他的工具, 比如 FriCAS (Axiom) 和 Maxima (也用过一段时间的 SageMath).

免责申明:

本文更多的应该是一个科普 (?) 小介绍, 不是如何使用 Mathematica 或者别的什么的教程.
(关于如何使用 Mathematica 的部分, 可以看 MMA 的不完全指南, 或者是 Mathematica and MultiParadigm Data Science 等)
实际上计算机代数系统是有限的, 它能代替的是已经有成熟解法的计算.
一些吐槽
- 经典笑话: 人工智能, 有多少人工, 就有多少智能.
- 成熟解法: 指的是可以有严谨表述, 清晰定义的解法, 一些 “一眼看穿”, “显然”, “易得” 的数学操作并不包含在其中.
我并不是很熟这些, 只是刚开始看而已. 所以没法很好的讲.
下面我加的这些历史和历史的解释完全就是我个人的瞎解释, 纯粹是故事性大于真实性. (请搞历史的手下留情)

一些计算机代数系统的介绍

计算机代数系统, 大家可以认为是那种自动挡的 “魔法” 武器, 比如可能有一个积分要去积分:

\[∫_0^1 P_l(x) \mathrm{d}x\]

(原题来自梁昆淼, 数学物理方程 (第四版) 10.1.11 习题, 下面除了特殊说明, 略去来源说明. )

你可以使用 Mathematica 来直接自动化这个积分:

Assuming[Element[l, Integers], Integrate[LegendreP[l, x], {x, 0, 1}]]

其返回的结果如下:

\[\frac{P_{l-1}(0)-P_{l+1}(0)}{2 l+1}\]

基本上不会超过一秒钟. 并且这个过程中你也几乎不必操心别的啥问题.

但是如果不太能够直接积分呢? 比如这个积分展开:

\[f(x) = x^4 + 2 x^3 ⇒ ∑ A_l P_l(x), A_l(x) = ∫_{-1}^1 f(x) P_l(x) \mathrm{d} x\]

这个时候直接进行积分:

With[{f = x^4 + 2*x^3},
 Assuming[Element[l, Integers], 
  Integrate[f*LegendreP[l, x], {x, -1, 1}]]]

这个时候就不一定能够积出来了… (这句话做保留, 万一那天真的成了, 我先膜为敬).

这里放一个刚开始用 Mathematica 的同学不会知道的没用小知识

如果 Mathematica 被你玩坏了, 那么请按下 Command-. (macOS) 或者 Ctrl-. (Windows) 来停止内核的计算. 虽然应该不是所有人都不知道吧…

那么这个时候可能就不太能自动档了, 所以你没准就会放弃计算机, 然后转战手工计算. 但是你也可以使用一下手动档:

已知结论: 多项式 $Q(x)$ 的广义级数展开不超过 $l \leq \mathrm{deg}(Q(x))$, 则可以积分到最高项停止:

With[{expr = x^4 + 2*x^3},
 If[PolynomialQ[expr, x],
  With[{m = Exponent[expr, x]},
   Table[
    Integrate[(2*l + 1)/2*expr*LegendreP[l, x], {x, -1, 1}],
    {l, 0, m}]],
  "Not Polynomial"]]

当然, 结果只是一个系数列表, 要还原的话, 可能还需要一些操作:

Simplify[Total[MapIndexed[#1 * HoldForm[LegendreP][#2[[1]], x] &, %]]]

那么最终的输出就是一个人畜无害的结果:

\[\frac{1}{35} (7 P_0(x)+42 P_1(x)+20 P_2(x)+28 P_3(x)+8 P_4(x))\]

(注: 稍微做了一些美化…)

这个时候, 你相当于是自己带着规则来进行一个计算化简, 赃活累活都交给了计算机. 但是如果你还想要更多的一些操作性, 比如说要积一个更加复杂一些的积分, 想要告诉 Mathematica 自己想要分部积分, 或者想要告诉 Mathematica 自己想要特殊的变换规则, 或者想要…

这个时候, 就不得不了解一些手动档的一些东西了.

这个时候的一个吐槽

这个时候, 你可能就会陷入一个非常痛苦的情况, 那就是规则太多了, Mathematica 帮你做得太多了, 而你没办法立刻了解这到底是个啥. (甚至很多时候花在弄清楚这个函数怎么用的时间, 可能就够你把这个函数积出来了, 并且考试又不用这个, 因为用得次数太少, 你也就忘了.)

并且更加坑爹的是, 有时候你花了大把心思写出来的自认为还算通用的函数, 结果不仅不通用, 并且在 Mathematica 里面竟然该死得早就实现了!!! 没错, 就是那个求特征方程本征值的东西, 前几天我为了做这个 pre 查 Wolfram 文档的时候, 竟然让我看到了这个东西! DEigenvalues (以及其对应的数值解函数 NDEigenvalues)

~~我去, 要是有这个~~

一些没啥用的历史

折叠了

最早的计算机代数系统是由诺贝尔物理学获奖者 Martinus J.G. Veltman 在 1963 年开发的 Schoonschip (用于计算 quadrupole moment of the W boson, W 玻色子的四极矩):

He (John Bell) became quite involved with what is now known as the Bell inequalities, while I started constructing my symbolic computer program Schoonschip. That also had its origin in the neutrino experiment: in doing the necessary algebra for vector boson production I was often exasperated by the effort that it took to get an error free result, even if the work was quite mechanical.

(from Martinus J.G. Veltman Biographical)

在 1984 年开始的 FORM 计算机代数系统可以看作是 Schoonschip 的延续版本, (如果我没有记错的话, 貌似在各大 ~~不一定是营销号的~~ 公众号里面, FORM 的作者要退休了, 可谓是没人维护的状态. 不过具体目前高能物理里面是啥情况, 等我讨论课上问了老师再说.) 其在高能物理里面应用比较多, 一个 Mathematica 和其的连接包可以参考作者的一个介绍.

一个吐槽

理论是美好的, 现实是残酷的. (bushi)

物理书院小组里面谈论问题的时候, 我提到了一个关于面包和芝士粘连关系的问题. 然后就被制止了: 因为太复杂了. 难道是面包和芝士很难组合在一起吗? 并不是, 复杂的问题在于, 哪怕理论很简单, 但是现实中要考虑的东西太多了, 也就导致了这个问题绝对不是一个简单小组讨论可以轻松结束的问题.

~~毕竟如果能够研究真空中的球形奶牛, 谁还愿意研究加热台上难以描述形状的芝士片啊…~~

等一下, 好像也不是不行

请仔细看看下面的这个问题:

考虑躺在加热台 $T_{\mathrm{h}}$ 上的一个圆柱形芝士薄片 (厚度为 $d$, 半径 $r$, 热容 $C$, 热导 $κ$), 周围环境认为是正常空气 $T_{\mathrm{c}}$ (暂时不考虑空气的温度差异), 于是有热传导方程 (和边值条件):

\[\left\{\begin{matrix}∂_t u - κ ∂_{xx} u & = & 0 \\u|_{t = 0} & = & T_{\mathrm{c}} \\u|_{ρ = r} & = & T_{\mathrm{c}} \\u|_{z = 0} & = & T_{\mathrm{h}} \\u|_{z = d} & = & T_{\mathrm{c}}\end{matrix}\right.\]

啊, 您不妨可以动手算算, (我觉得应该不难… ), 不过我算到一半被打断了, 因为做实验的时候出现了问题… 啊, 这个是题外话, 总之最后我没算下去, 用 COMSOL 草草算了个温度分布 (文件见这里) 就去做别的事情了:

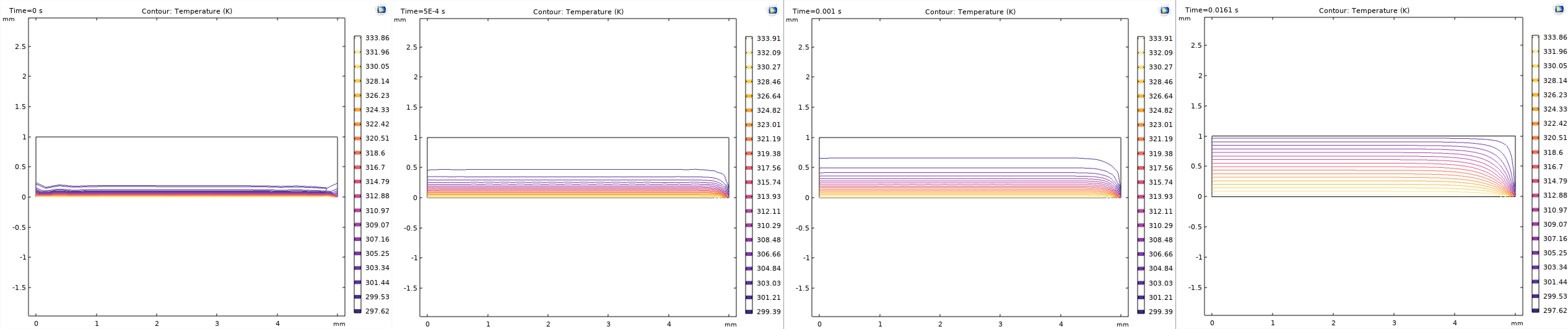
/_img/pieces/comsol-cheese-simulation-heat-temperture-60-env-temperture-27.png

关于这个的数值求解, 我会在 FEM 的部分简单介绍一下的. 不过这里再吐槽一句: 淦, 模拟精度要上去的话, 电脑吃不消啊! ~~MacBook Air 你可是真是狗啊!~~

数学的简单美, 我觉得可能有三个原因:

考虑的问题简单, 或者说没有把问题展开来, 还没看到肮脏的地方就下一步了. ~~中华武功, 博大精深, 点到为止~~ (不过这应该情有可原, 毕竟这些赃活不太适合美丽的数学)
省去了许多的约定, 默认你懂了.
有许多或者归纳或者直接构造的美妙的定理 (或者像物理里面的第一性原理一样的东西? )

(注: 上面的一定不对, 请数学系的手下留情.)

这些计算机代数系统的开发基本上都是为了能够解决某一特殊领域的具体问题, 所以相比 Mathematica 这样的巨大的计算系统, 它们的性能会更好一些. 当然, 还有一些开发出来的代数系统更多是为了教学用, 比如 emmy (scmutils 被用于给一些物理系学生提供一种推数学公式以外的想法).

当然, 像从前人一样从零开始构建一个符号计算系统, 哪怕是为了对某种方程, 某个问题进行特化, 现在看来也是挺 (帅的) 没用的, (计科导的约当标准型就很牛). 可以在现有的符号计算系统基础上构建, 我觉得这样会更加的合理一些. ~~毕竟现在已经过了茹毛饮血的时代了~~

下面部分会介绍这样的符号计算系统可能是如何构建的, 以及它们背后的一些算法是如何实现的.

一个计算机代数系统的简单构建的说明

Normal Forms and Algebraic Representations

小学生都会的加法 $1 + 1 + 2 = 4$, 对于在座的肯定是口算的. 像我这样稍微笨一些的, 用最原始的方法 $(1 + 1) + 2 = 2 + 2 = 4$, 也是可以做出来的. 稍微笨一点的方法, 交给计算机来实现, 也是可以实现的:

MOV 1, AX
ADD AX, 1
ADD AX, 2                       ; AX = 4

但是如果稍微加一些活 $x + y + 2 x$, 那么这个时候, 这种笨方法就可能不太适用了: $(x + y) + 2 x$, 那么 $x + y$ 是什么? 也许你会说, 直接交换不就好了, 法国小学生 (幼儿园? ) 都知道加法是一个可交换的 Abel 群. 但是计算机并不知道可以这样, 或者说, 假如你写了这样的一个规则 (假设 $e_i$ 为表达式, $λ, μ$ 为数, $x$ 为任意符号):

$e_1 + e_2 = e_2 + e_1$
$e_1 + (e_2 + e_3) = (e_1 + e_2) + e_3$
$λ x + μ x = (λ + μ) x$

于是计算机就会在执行加法的时候对相加的元素进行一个两两配对, 然后尝试相加… (那么如果有一个包含 $n \gg 1$ 个元素相加的表达式… $C_n^2 ∼ n^2$)

也许在量子计算机这种可以单周期计算所有组合的大杀器出来之后, 这样的规则估计是可行的. 显然需要一个更加合理的方式来处理这些规则, 需要能够用来更好地匹配规则.

这里还有另外的一个小注记

那么, 如果更加吹毛求疵一些的话, 如果这个加法它不可交换… (虽然我也想不到啥奇葩加法不可交换, 可能是我数学太烂了.)

或者是这里的 $λ$ 和 $μ$ 并不是那么简单的一个数, 比如 $y x + x z$, 而是一个符号常数. 或者是别的什么. 那么这个时候, 这个规则就需要更加细致的一个修改了.

这么说, 应该可以理解为什么大部分的符号代数系统都会介绍一个群环域, 都会介绍多项式理论和多项式化简之类的问题. (实际上接下来的算法里面, 也有许多需要多项式因式分解的理论).

(这里对上面愚蠢的说法进行一个修正: 因为加法和乘法在常见的代数结构中是非常基础的运算, 由这两个运算组成的多项式结构在化简, 计算中起到的作用非常的大. 所以通过研究它们的运算性质, 可以对之后的理论和实践会有很多的用处. )

~~不过可能还是那个经典笑话: 你已经学会了加法和减法了, 现在…~~

那么这里可以做一个看起来不太自然的约定:

将运算符看作是一个函数 $f: x \mapsto f(x)$:
- $x + y ⇔ +(x, y)$
- $f(x), h(g(x), k(y), z, …)$ 等等
将表示为 $f(x_1, …, x_n)$ 形式的表达式做成树

关于这样约定的历史原因

因为一开始大部分的 CAS 都是从 MIT 的 AI Lab 里面出来的, 而 MIT 的 AI Lab 恰好也产出了一个编程语言 Lisp (其发明的目的也确实是为了进行符号运算, 如果想要了解更多, 可以等等看我的一个介绍性的博客: From Linked List to the Old Yet Modern Computer). 这些早期的 CAS 或多或少地都有受到 Lisp 的一些影响.

一个例子就是如果你在使用 Mathematica 的时候, 会发现 List 是从 1 开始的. 而如果你好奇 (或者不小心) 试过去访问 0 的元素的话… 你就会发现会读到一个看起来比较奇怪的东西:

(1 + 2)[[0]] (* => Integer *)
{1, 2, 3}[[0]] (* => List *)

实际上应该是可以把结果 3 看作是 (Integer 3) 这样的东西. 把 {1, 2, 3} 看作是 (List (Integer 1) (Integer 2) (Integer 3)) 这样的东西.

表达成树相当于只是给了表达式一个更好的表示方法, 虽然还挺简单的, 但是可以被折腾出非常多的可用的应用空间: 比如用于符号表达式的回归: PySR: High-Performance Symbolic Regression in Python and Julia; 或者可以看 Algorithms for Computer Algebra 中的第三章: Normal Forms and Algebraic Representations.

实际上这样还有一个好处就是在之后可以通过 0 位置上的元素来决定如何约化表达式. 也就是下面介绍的类型规约.

而 Lisp 则受到了数学中的 Lambda 算符的一个影响. (比如可以参考 [[/reading/calculi-of-lambda-conversion/][[Reading] The Calculi of Lambda Conversion]]) 这样的前提的表示方法还可以被更加抽象一点地表示: 将 $λ a.(λ b. a + b) x y$, 看作第一个部分 $λ a. (λ b.a + b)$ 得到的是一个函数 $λ b.(x + b)$, 最后得到的是一个值. 为了简单, 可将其简写为 $λ a b . (a + b)$. 这样操作的结果就是可以在每一步里面加入类型规约 (Typed Lambda).

这种类型规约更像是前面介绍的两个不同类型的东西乘在一起, 如何进行化简和变化的一个规则的感觉.

这样约定之后, 对于一个表达式 $(2 y + 4 t) × x$, 就可以变成:

$/_img/pieces/symbolic-math-equation-as-tree.svg$

大概是这么个理… (实际上要稍微复杂一些)

那么虽然有了树, 但是并不意味着问题就解决了, 比如 $2 x - 2 x + y$ 和 $y$ 是等价的, $sin^2 k x + cos^2 k x - sin^2 j y - cos^2 j y$ 和 $0$ 是等价的 (等等); 再比如 $x^2 - y^2$ 和 $(x + y)(x - y)$ 是等价的, $12 x^2 y - 4 x y + 9 x - 3$ 和 $(3 x - 1) (4 x y + 3)$ (等等). 但是在表达式的树的角度上看则并不是这样的, 于是出现这样的需求: 能否有一种将各种表达式的树都变换成最正规 (Normal, 一般可能应该翻译成正则?) 的形式. 这样的话就能够解决上面出现的一些问题:

零表达式判断
展开式还是因式分解式

具体的可以看 Normal Forms and Algebraic Representations 里面的说明, 这里截取一个上面书中对于展开式的正则形式 (Normal Form) 的定义:

Definition: An expanded normal form for polynomial expressions in a domain $D[x_1, …, x_{ν}]$ can be specified by the normal function:

$f_1$:

(i) multiply out all products of polynomials

(ii) collect terms of the same degree

An expanded canonical form for polynomial expressions in a domain $D[x_1, …, x_{ν}]$ specified by the canonical function:

$f_2$: apply $f_1$, then

(iii) rearrange the terms into descending order of their degrees

~~(抱歉, 现在你问我为啥我也不能解释, 这本书是我最近找到的, 刚开始看, 请谅解. )~~

这里统一将其概括为一个表达式化简问题 (simplify).

关于表达式化简问题, 这里截取 An on line program for non-numerical algebra 里面对于一个简化函数的描述图片:

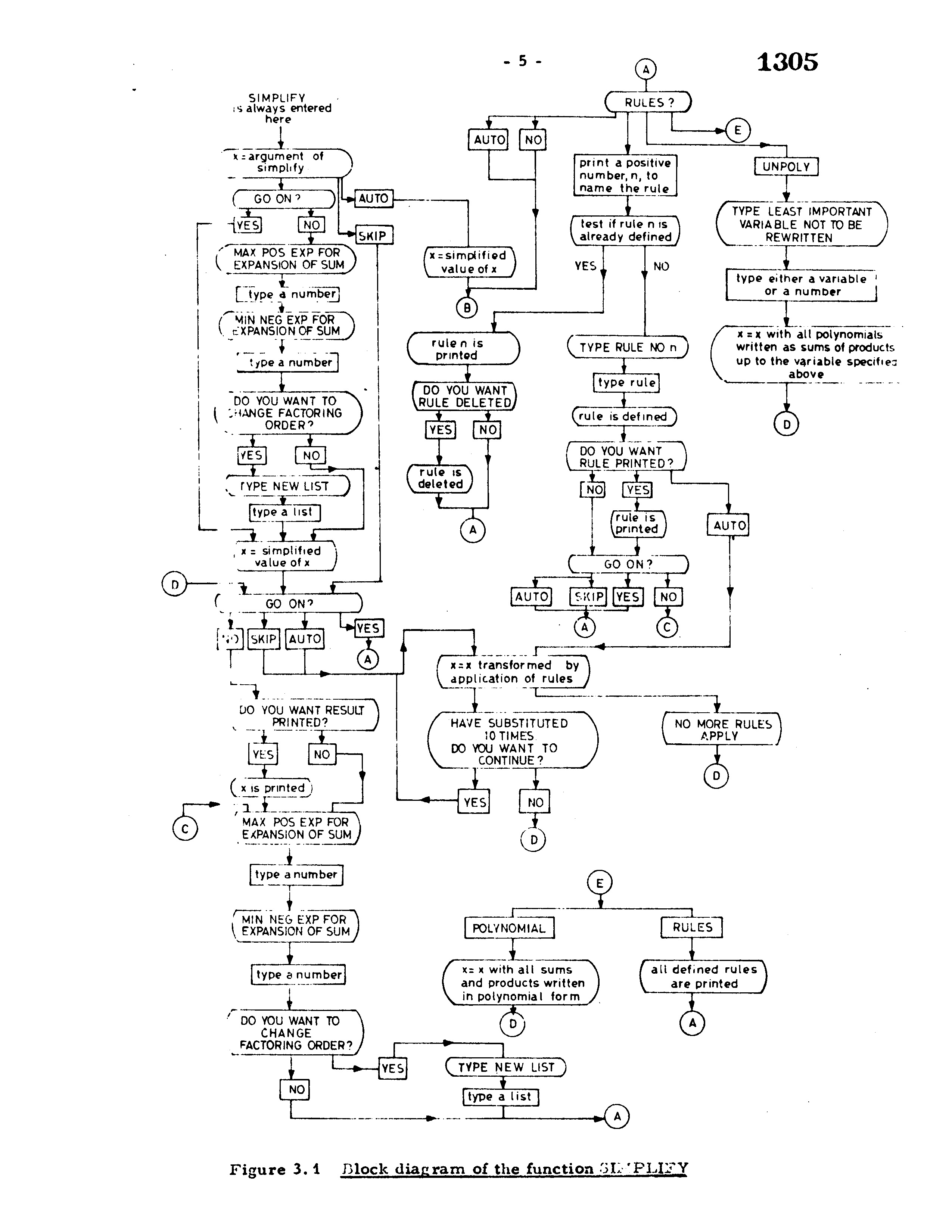
/_img/pieces/korsvold1966.jpg

(虽然图不是很清晰… 并且这个算法也很老了.)

文献和实际的一个对应

这样的化简函数, 或者是前面的展开式的最简判定, 实际上可以在很多的计算机代数系统中看到. 比如在 Mathematica 中常用的 Simpilfy 和 FullSimpilfy. ~~虽然它不一定能按你的想法化简就是了~~
或者说, 如果你想要一些更加具有自定义能力的化简的话, 可以尝试 Maxima 中的化简操作. 这里列举一些:
可以通过对函数添加 property 来对化简程序提供进一步的信息说明.
- declare(f, additive) 可以使得函数对于加法保持运算
- declare(f, linear) 可以使得函数为线性函数
- declare(f, antisymmetric) 使得函数反对称
- …
从实现上来说, 可以将函数存放在一个环境表中 (association-table), 函数名称对应的是一个属性列表 (property-list):
```
(defparameter *math-env*
  '((f . (:additive T :linear NIL ...))))
```
并且可以在表达式树的节点加入根据子节点属性推理约束的局部属性. 而为了性能, 可以引入类和先编译后执行, 就像是 Axiom/FriCAS 做的那样. 不过这些都是一些工程上的 “肮脏” 实现了.
或者干脆就直接用编程的一个逻辑, 比如 SymPy 里面的 sort_key.
或者更加底层一些, 可以尝试 Axiom/FriCAS 的 rule, Is 这样建立在底层规则匹配和映射规则的符号计算系统. (文档)
```
evenRule := rule cos(x)^(n | integer? n and even? integer n)==(1-sin(x)^2)^(n/2)
evenRule(cos(x)^4)
```
或者是
```
eirule := rule integral((?y + exp x)/x,x) == integral(y/x,x) + Ei x
eirule(integral(sin u + exp u/u, u))
```
(注: 需要注意 Axiom 和 FriCAS 的运算符号可能有一些细微的区别, 并且这里的规则可能并不是那么炫酷就是了. )

实际上这个规则的映射和匹配是接下来我想要介绍的一个重头, 但是突然想到一个事情: 好像我不是很会用 FriCAS 这个软件… (最近查文献接触到的)

那么有了表达式的树和正则表示, 接下来的就是根据正则表示的表达式, 进行匹配, 识别表达式对应的类型, 并按照相应的类型对应的规则去变换表达式, 达到计算和化简的目的.

Mapping and Integration Rule

一些历史原因

从最早的计算机编程语言 (?) Plankalkül 可以看到数学的逻辑推理系统在当时的巨大影响力, 一些程序语言的设计都保留着逻辑推理的影子: $P → Q ∧ P ⇒ Q$.

因为数理逻辑是研究数学证明的证明, 在构建早期的计算机系统 (或者说第一代人工智能) 的时候, 人们希望的是能够让机器学会数学的证明 (逻辑推导能力).

或者换一个说法, 在数学里面经常会听到这样的说法吧: A 是这样的一个 A, 它满足条件 $P$, 当且仅当 $Q$, 我们称这样的 A 为 A. (不懂数学, 大概是这样吧…) 于是逻辑学将其描绘为 $A : P ↔ Q$, 然后计算机科学家则希望弄一套能推理这个逻辑的系统, 于是像 ACL2, Z3 这样的自动命题证明 (ATP) 程序就出来了.

于是可以看到, 计算的一个方式就变成了从 $A ⇒ B$ 的这样的一种因为输入满足条件, 于是根据已有规则 (定理), 映射对应到规则所约定的形式去:

规则:

\[L(f): f(λ x + μ y) = λ f(x) + μ f(y)\]

输入满足条件:

\[L(g)\ \mathrm{is}\ \mathrm{true}\]

结论:

\[L(g) = \mathrm{true} ∧ g(2 x + 3 y) ⇒ 2 g(x) + 3 g(y)\]

(感觉解释得好牵强… )

不过实际上的对应规则肯定没有这么简单就是了.

假如想要积分, 可以去查表 (比如中科大有一本积分的方法与技巧, 反正我是没看过), 那么这个查表的过程就是一种匹配的过程: 当前要积分的部分和表中的那一项是一样的, 或者是当前要积分的部分是否有部分可以在表中找到等等.

以 Rubi (A Symbolic Integrator Built on a Rule-Based If-Then-Else Decision Tree) 为例的规则穷举的符号积分, 干的差不多就是这个事情. 好处是这样的做法竟然出奇的快 (不要小看计算机的匹配速度啊! ), 坏处就是提升的空间只有疯狂扩展积分表.

这里的一个技术说明

害, 还技术说明呢…

如果去翻 Rubi 的代码或者是说明的文档, 可以看到其积分方法是如下定义的 (以 Bessel 函数为例):

\[∫ J_1(a + b x) \mathrm{d}x → - J_0(a + b x) / b\]

Int[BesselJ[1, a_. + b_. * x_], x_Symbol] := - BesselJ[0, a + b * x] / b /;
FreeQ[{a,b}, x]

一个注释: 这里有一个比较 tricky 的事情就是 Mathematica 的函数定义是规则匹配的, 比如你可以这样定义一个 Mathematica 的函数:

p[0] := 1;
p[1] := x;
p[n_Integer] := ((2 * n - 1) * p[n - 1] - (n - 1) * p[n - 2]) / n;

于是你就定义了一个由递推公式定义的 Legendre 函数了.

关于匹配的问题

为了匹配一个表达式, 最简单的做法就是在树上挖孔, 然后把表达式填进去. 一个好处是当前的树是正则形式 (Normal Form), 所以就应该 (?) 可以比较轻松地解决这个问题.

但是可能还会出现一些比较困难的问题, 比如说在匹配的时候, 是存在 callback 的: Int[BesselJ[1, a_. + b_. * x_], x_Symbol] 这个匹配里面, 就要求在树的两个节点中, 都要包含相同的子节点 x. (callback 可能会导致匹配的死循环)

关于在树上的匹配, 可以参考的关键词: tree regexp.

当然, 除了直接的匹配, 还有一些是通过别的方法, 比如类似于构建一个特殊的空间来计算表达式之间的距离的方法: Math Expression Retrieval Using an Inverted Index Over Symbol Pairs.

(等等)

类似的:

Int[BesselJ[n_,a_.+b_.*x_],x_Symbol] :=
  - 2 * BesselJ[n-1,a+b*x]/b +
  Int[BesselJ[n-2,a+b*x],x] /;
FreeQ[{a,b},x] && IGtQ[(n-1)/2,0]

\[∫ J_n(a + b x) \mathrm{d}x → - \frac{2}{b} J_{n-1}(a + b x) + ∫ J_{n-2}(a + b x) \mathrm{d}x\]

那么你也可以定义自己的积分函数和积分方法了, 只不过可能不一定能覆盖到所有. (是不是很简单? ~~可能并不是~~)

上面的这个积分可能看起来太简单 (具体) 了是吧, 其实也可以写一些更加抽象和复杂一些的规则:

\[∫ \frac{(a + b F(c \frac{\sqrt{d + e x}}{\sqrt{f + g x}}))}{A + B x + C x^2} \mathrm{d}x → \frac{2 e g}{C (e f - d g)} \mathrm{subst}(∫ \frac{(a + b F(c x))^n}{x} \mathrm{d}x, x, \frac{\sqrt{d + e x}}{\sqrt{f + g x}})\]

Int[(a_. + b_. * F_[c_. * Sqrt[d_. + e_. * x_] / Sqrt[f_. + g_. * x_]])^n_. / (A_. + B_. * x_ + C_. * x_^2), x_Symbol] := 2 * e * g / (C * (e * f - d * g)) * Subst[Int[(a + b * F[c * x])^n / x, x], x, Sqrt[d + e * x] / Sqrt[f + g * x]] /;
FreeQ[{a, b, c, d, e, f, g, A, B, C, F}, x] && EqQ[C * d * f - A * e * g, 0] && EqQ[B * e * g - C *(e * f + d * g), 0] && IGtQ[n,0]

(注: 实际上还有更加复杂的. 可以去看看 Rubi-5.m (基础性代码函数定义, 结构更加清晰), 以及可以去看看更多详细的规则定义 (旧版本, 主要是规则说明))

当然, 上面的这样的规则仍然是比较简单和美观的积分规则, 实际上想要覆盖更加广泛的规则, 想要构建更多的积分规则的话, 还需要更多的处理 (比如 Intxxx 的代码).

但是这样的单纯查表实际上也是有极限的. (可以看看这个检测报告: Computer Algebra Independent Integration Tests (Summer 2022 edition))

关于这个检测报告

啊, 怎么说呢, 也不是那么极限吧, 毕竟从报告上看, 除了数量上不如 Mathematica 这样的变态大杀器, 在最简结果的角度上看, 这样的查表法也不算是失败的.

~~怎么又是一种力大砖飞的即视感~~

但是让人可能有些置疑的是关于这个测验用的积分试例, 因为选用的是 MIT 的 integration bee (不愧是大学校, 玩的真花) 的试题, 应该是有些偏向性的… (不过要是都通不过, 好像也没啥可比性).

如果没有一个巨大无比的积分表的话, 那么想要干掉一个符号积分, 剩下的就只有靠数学家来构造一些巧妙的算法.

从简单一些的有理函数积分 $∫ \frac{q(x)}{r(x)} \mathrm{d}x$, 其手工积分的通法大概就是做因式分解: 得到 $∫ \frac{1}{a + b x + c x^2} \mathrm{d}x$, $∫ \frac{1}{a + b x} \mathrm{d}x$, $∫ C \mathrm{d}x$, $∫ \frac{p x + q}{a + b x + c x^2} \mathrm{d}x$. 于是问题归化为因式分解和有理函数的分解问题. 但是有理函数的多项式分解并不是很好做, 并且完全化简在计算的时候看起来并不是很快 (指对计算机). 所以有 Hermite (专门的链接暂时没找到, 可以看 Integration of Rational Functions) 和 Horowitz-Ostrogradsky 方法:

Hermite Method $∫ \frac{q_i}{r_i^i} = ∫ \frac{q_i a + (q_i b)' / (i - 1)}{r_i^{i-1}} - \frac{1}{i - 1} \frac{q_i b}{r_i^{i-1}}$
Horowitz-Ostrogradsky Method: 通过待定系数法将问题变成线性方程组, 即 $∫ \frac{q}{r} = \frac{q_1}{r_1} + ∫ \frac{q_2}{r_2}$

(其实最后还是一个多项式因式分解的问题… ~~还是群环域…~~)

最后, 还有一个经典的算法 Risch Algorithm.

(下面的介绍参考自 The Risch Integration Algorithm, 但是看得不够细, 没啥解释)

Differential Algebra
Transcendental Elementary Functions
Logarithmic Extensions
Exponential Extensions

更多详细的内容可以去参考:

Symbolic Integration I
计算机代数系统数学原理 (Math$μ$)

Equation Solve

既然已经拥有了积分, 求导, 化简表达式, 匹配表达式的能力, 那么就可以去解方程了吧.

求导的说明

啊, 这, 求导的规则其实比较简单的吧 (笑):

\[(∑ f_i)' = ∑ f_i'\]

\[(∏ f_i)' = ∑_j ∏_{i ≠ j} f_i'\]

\[(f(g(x)))' = f'(g(x)) g'(x)\]

实际上这个求导规则是可以比较轻松地去实现的. 可以参考 SICP 的第二章的例题. (或者等我有空了把之前读的代码整理一下…)

原则上来说, 按照数学物理方程的这个套路来进行一个方程求解:

将输入的方程进行一个标准化 (计算 $Δ$, 然后根据 $Δ$ 计算标准形式)

一个注记

$/_img/pieces/math-phy-equations-overview.svg$

(defun cal (exp)
  (let ((Δ (cal-Δ-of exp)))
    (cond ((> Δ 0) (cal-hyperbola-of exp))
          ((= Δ 0) (cal-parabola-of  exp))
          ((< Δ 0) (cal-ellipse-of   exp)))))

可以看数学物理方程 (期中的复习笔记).

将标准形式和规则表里面进行一个匹配, 若存在匹配的就按照规则进行处理.
基本操作应该就是分离变量后按照边界条件进行展开 (积分), 或者是施加积分变换去求解多项式方程等等.

一个更加详细的介绍如下:
- 首先根据方程类型去提取系数:

[可以参考 Symbolic Solutions of PDEs 是 Mathematica 的符号偏微分方程的一个用法.]

其他的一些注记

Symbolically Solving Partial Differential Equations using Deep Learning 通过深度学习的方法来求解偏微分方程.
Neuro-symbolic partial differential equation solver 通过符号偏微分方程来加速神经网络计算的一个应用. 好处估计就是可以让搞人工智能的那帮卷怪来加速偏微分方程符号计算的开发了.

Numerical Methods

[当然, 符号计算是有极限的, 那么仍然大可以进行一个数值计算: (Numerical methods for partial differential equations)]

FEM (可以看看之前的一个科普 Dot, Dot, Dot and …, 或者是 COMSOL 的一个简单介绍, 虽然也鸽了)
FVM (比如流体力学里面的欧拉方法)
… [来不及了, 没时间详细写了.]

End

最后, 很遗憾, 这里基本都是别人做的东西, 没啥我做的东西. 并且迫于生活压力, 虽然计算机代数系统这个我很早就开始折腾了 (Computer Algebra PickUP), 但是中间迫于生活压力和要寄微积(分), 所以鸽了. (欸嘿)

并且这里介绍的这些大多都是一套非常旧 (基本都是上世纪的大牛作品了) 的逻辑推理方法的计算机代数求解系统, 实际上还有一些新的工作, 比如通过机器学习和其他方法结合的方式, 给旧的逻辑系统增加新的更多的功能.

除了文中粘贴的链接可以去尝试爬文献, 还有一些别的文献和阅读资料可以看:

Macsyma: A personal history (Macsyma 的个人回忆性质的历史记录)
- Macsyma 是一个非常早期的计算机代数系统. (可以参考 Wolfram 的回忆) 其后继由一位叫做 William Schelter 的大佬独自维护 (~~不过因为万恶的版权, 在 Symbolics 没了以后很长一段时间之后才搞定了 GPL 协议放开了 Maxima 的源码~~), 其叫做 Maxima.
Mathmu (清华之前的学生 ~~以及现在我们的一些老师~~ 做的一个计算机代数系统)

符号计算的一个介绍