或者说, 关于”凉凉”这个名字的来历的故事

群里面有个老师发现了我的网名”凉凉”的来历. 其实并不是一个非常神秘的东西, 说白了, 其实就是以前的同学互相喊名字的时候, 舌头打结了, 谐音成了”凉凉”了.

舌头打结了

所以这篇文章, 我要为”舌头打结”这个事儿正个名 – 舌头打结其实不仅可以说得非常得高大上, 并且还能玩出花活来.

舌头打结的高级说法

我翻找着自己的语文知识, 为您端上一桌”舌头打结”的高级说法:

合音

诸:
文言「之於」, 「之乎」的合音字. 如: 「藏諸名山」, 「付諸流水」, 「反求諸己」, 「付諸行動」.
来源: 教育百科

为了给”舌头打结”正名, 我失去的语文突然被那一点点的脸皮唤醒了. 对了, 就是这样, 就是那个叫做合音的东西! (那个让我古文阅读选择题岌岌可危的东西. )

而类似的合音还有其他的有趣的字眼: “嫑”(biáo, 即”不要”), “覅”(fiào, 还是不要)等. ~~看来大家拒绝的时候都很干脆(bushi)~~. (如果还想要了解更多的话, 可以参考知乎: 有哪些有趣的合音字, 或者去翻看古汉语的书. 我不便多多举例, 以免言多而失. )

切音(反切)

切音:
古代中文用兩字併成一音的注音方法. 上字取它的聲, 下字取它的韻與調. 如信的切音為息晉切.
来源: 教育百科

既然前面有两个(或以上)字可以合成一个新的字, 所以类似的, 为什么不把一个字拆成两个字呢? (多么深厚的中国汉字啊… ~~多么惨淡的语文考试啊…~~)

这就是一种古代给文字注音的方式了. 虽然一开始写作”X, AB反”, 但是随着历史的发展, 为了避讳, 渐渐变成了”X, AB切”或者”X, AB翻”. 看见古书中的”X, AB切”时, 只需将”A”的声母和”B”的韵母(一半含有介音, 也就是”liáng”中的”i”这样的非主要元音的元音. )和声调相结合, 就能够得到”X”的读音了. (参考资料: 中国大百科全书)

一个简单的例子: 在《康熙字典》(在线)中:

凉：《唐韵》《集韵》《韵会》𠀤吕张切，音良。《正韵》凉，通作凉。《韵会》薄寒爲凉。《前汉·五行志》𡯎凉，冬杀也。《注》师古曰：凉，薄也。

(注1: 如果有显示不出来的字样… 那应该是当前字体不支持的生僻字, 我这里也不太能够显示, 所以不好意思. )

(注2: 在切音中, 用的一般是古音而非现代的发音. 所以有时候并不是非常好懂. )

注音

注音:
中国在民国时期第一套法定的汉字式拼音字母. 又称国音字母, 注音符号.
来源: 中国百科全书

上面的切音着实有一些让人不知所措 – 毕竟, 切音有点像是一种文字趣味小游戏, 不够通用(一个字可以有多个切音的写法), 也不够现代(毕竟很多字的读音在历史的发展中已经逐渐演化了, 更别说我家乡一条街里面都能有不同的”方言”. ). 于是注音符号就出现了, 用特定的字符代表响应的音节:

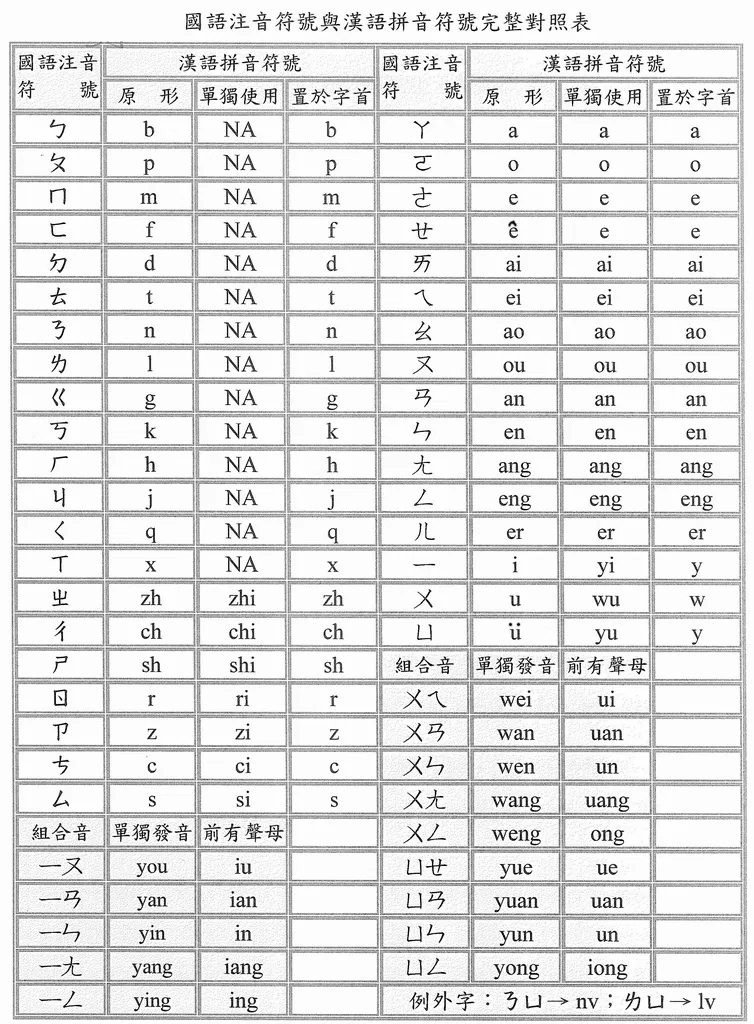
(图片来源于网络)

到了这个时候, 注音已经和现代的拼音十分类似了, 用一些音节组合在一起, 然后根据特定的节奏和音调, 就能够发出对应的声音. 尽管这套注音方式目前很少见, 但是还有台湾省仍在使用, 并且在一些的汉语词典中也能够看到.

(不过关于这个, 我在找资料的时候还看到一个比较有意思的新闻: 网易的游戏天谕中有一个精灵语, 就是用注音来表示的文字. 于是专门有玩家去发帖翻译, 然后台湾的玩家就吃瓜了. )

之于拼音, 应该就无需多言了. 但是都可以发现, 一段声音可以被拆分成几段简单的音节的混合. 那不就是藤田咲和…

(图片截取自官方的Youtube, 注: 不愧是夹心酱, 哪都吃瘪. 官号的片段还不如粉丝的播放量多, 乐. )

似是时候掌握一门”“舌头打结”“的技术了

那么不想来掌握一门创造声音的秘籍么?

声音是一种摇摆

众所周知, 只要你按一定的频率摇摆, 就会形成声音.

扭啊扭

(图片来源于维基百科, 这个新奇玩意不太熟, 感觉有些好玩. )

如果我们用摇摆的程度 – 比如上面那个电摇小子扭动的幅度作为纵轴, 并以横轴为时间, 画在纸上, (一个简单的)形式很可能就会像下面的图一样:

简谐振动

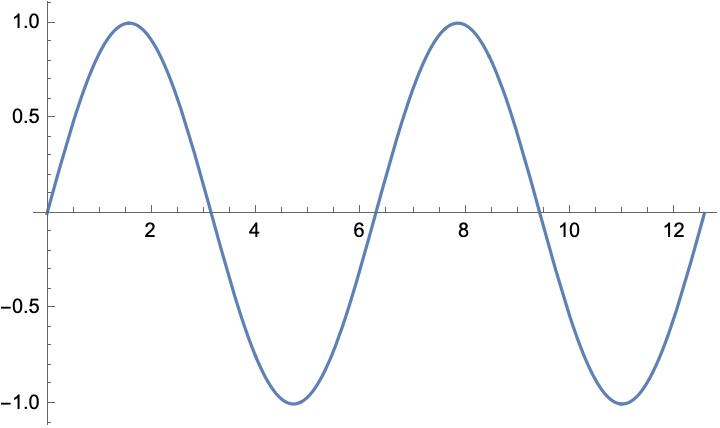
(以上图片由Mathematica绘制)

于是当我们”摇摆”起来时, 我们就产生了振动 – 同时也就有了声音.

一个音符

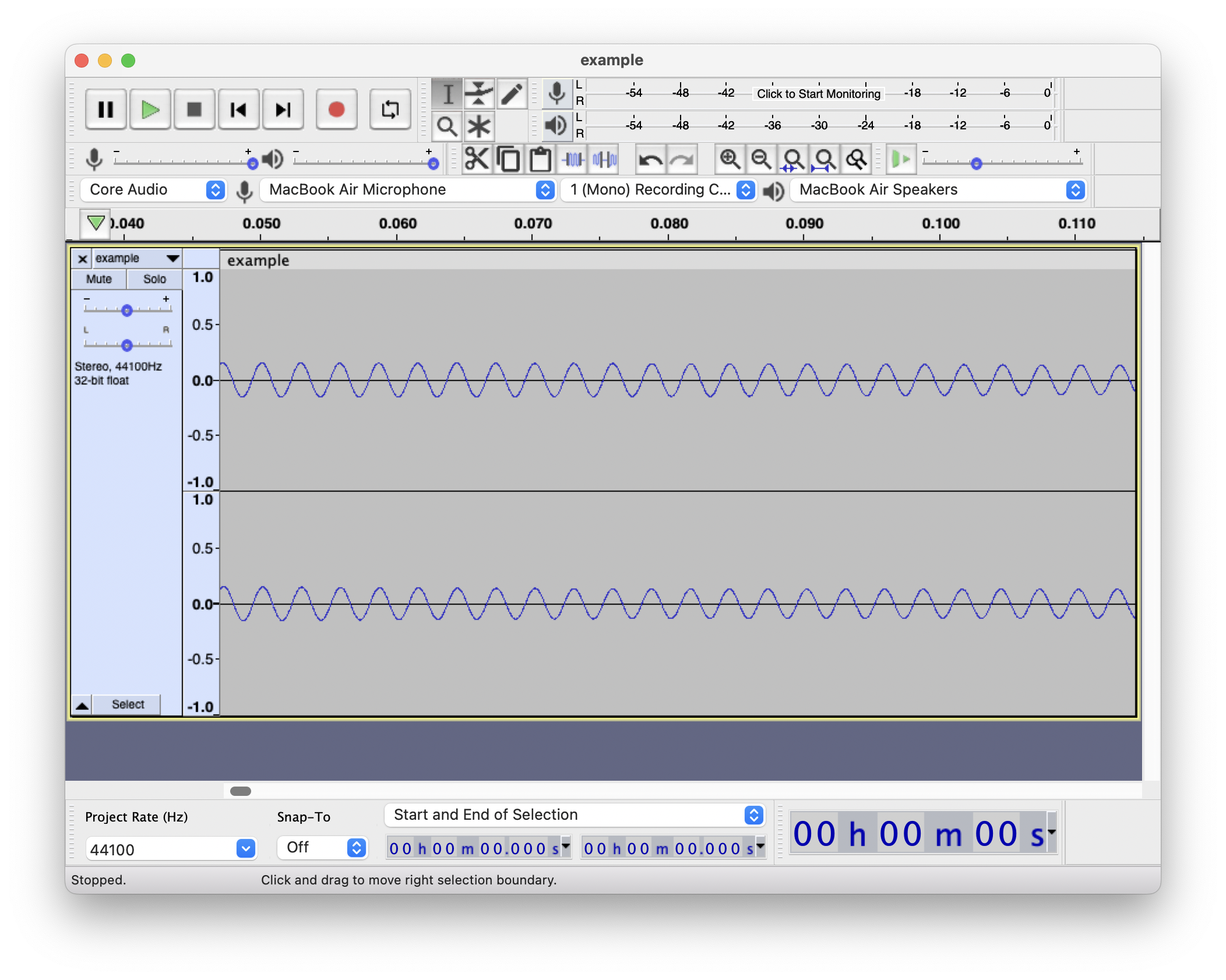
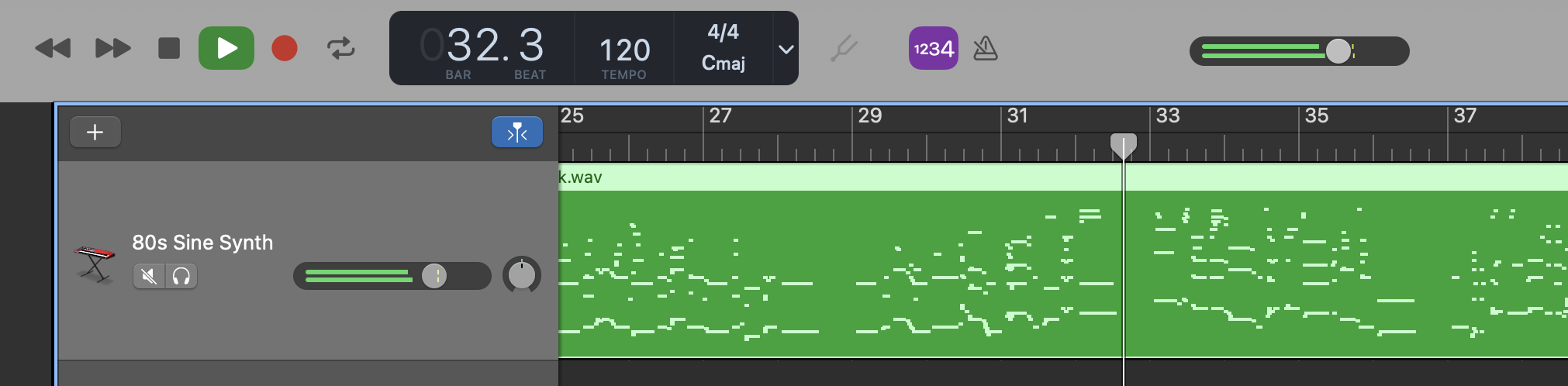
(以上由 Audacity 查看, 音频由 GarageBand 生成, 音色为 80’s Sin Synth. 音符据大佬说是fa, 也就是简谱的4. )

(注: 之所以专门挑选了这个音色, 是因为这个正弦合成器发出的是类似于三角函数的振动. 这样的振动因为其变换形式简单, 所以也被叫做简谐振动. 通过合成器生成周期性 – 或者说按一定频率改变的声音信号, 最终形成了我们听到的音乐的声音. 哦, 对了, 还有合成的节拍器的声音. )

而不同的物体的摇摆的频率并不相等, 每一种物体都会有一个自己的”固有频率”. 以一台调好音(中央C之上的A的频率为440Hz)的钢琴为例, 其中央C的频率即为261Hz左右.

当然我们听到的声音并非都是纯粹的单一频率的声音, 比如在很久以前, 我从我的同学那里得到了一支口琴 – 当我蹩脚地吹出一首小星星之后, 他用五味杂陈的表情对我说: 你把边上的孔都吹响了, 声音都混在一起了… (哈哈哈) 于是我的声音就像是几个音混合在一起的振动的感觉:

混合的振动

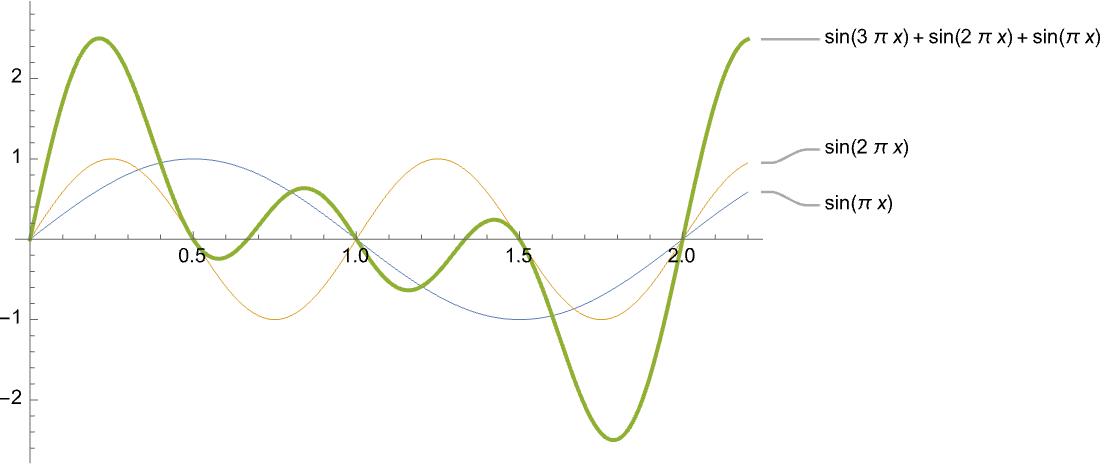
(以上图片由Mathematica绘制, 图中的例子是我瞎掰的, 现实的例子则是我的主音吹走调了… )

而在现实中, 如果我同时按下一组琴键, 就会得到一个混合的声音 – 学音乐的估计会说这叫做和弦.

Dm和弦

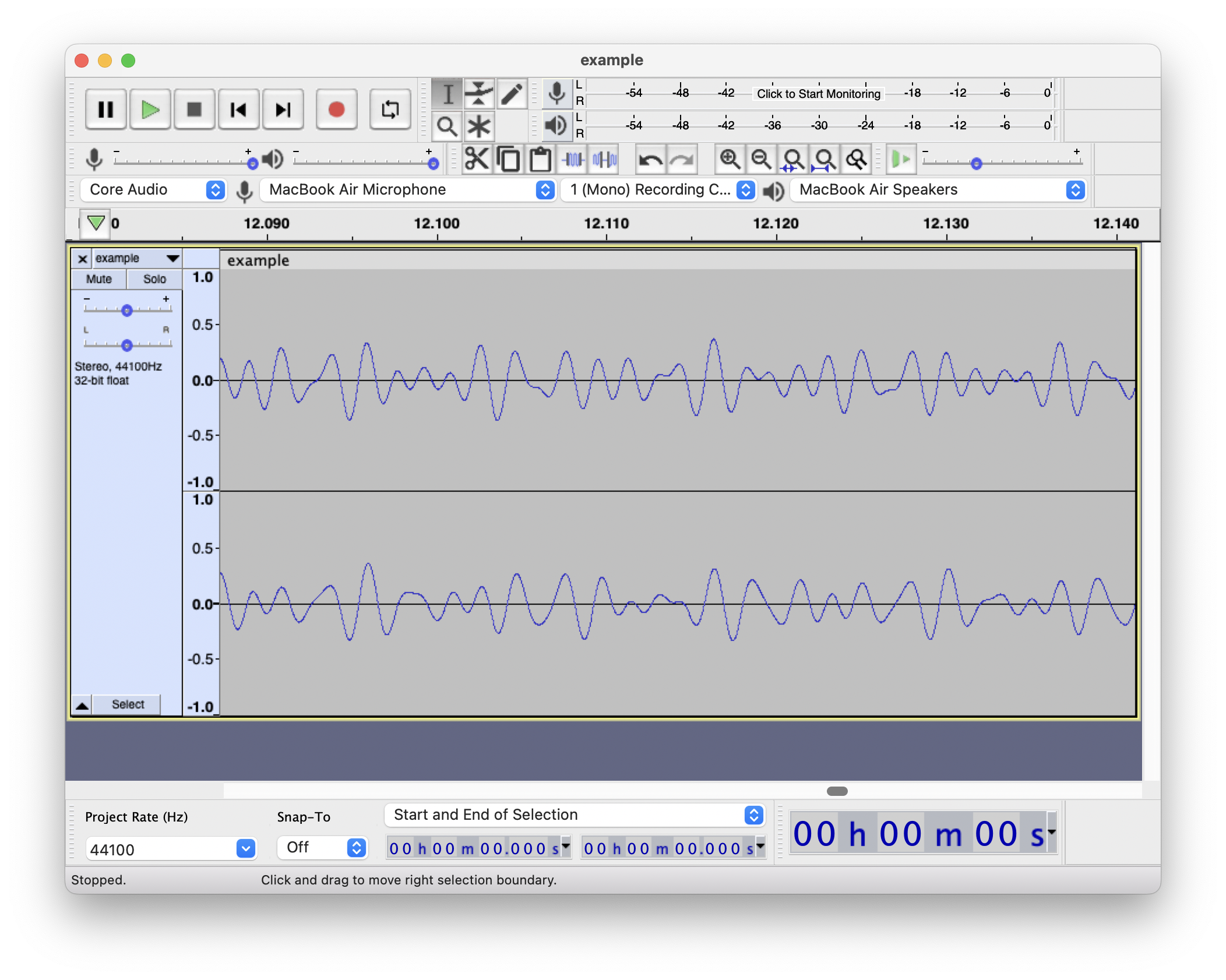
(以上由 Audacity 查看, 音频由 GarageBand 生成, 音色为 80’s Sin Synth. 和弦据 GarageBand 显示应该是Dm. )

所以并不是说不纯频率的声音就是一种不被需要的声音, 音乐中的和弦就是多种单音的复合的声音, 能给人一种和谐的感觉.

同样的, 在我们敲击钢琴中央C琴键的时候, 钢琴发出的声音也并不是只有纯粹的261Hz声音, 而是同时也混有其他的频率的声音 – 于是这样的声音就形成了钢琴特殊的音色. 这就好像是同样一句话, 同样的读音, 但是不同的人却会有不同的音色.

(以上图片由Mathematica绘制, 源音频文件由Synthesizer V Studio Basic使用AiKO Lite生成. 源音频见后面文章. )

所以, 是简谐振动的分解与合成

虽然前面的注音, 切音, 以及平时常见的拼音, 看(听)起来更像是将一段声音拆分成几段音节的混合. 然后像拼积木一样拼起来, 就像是下面这样:

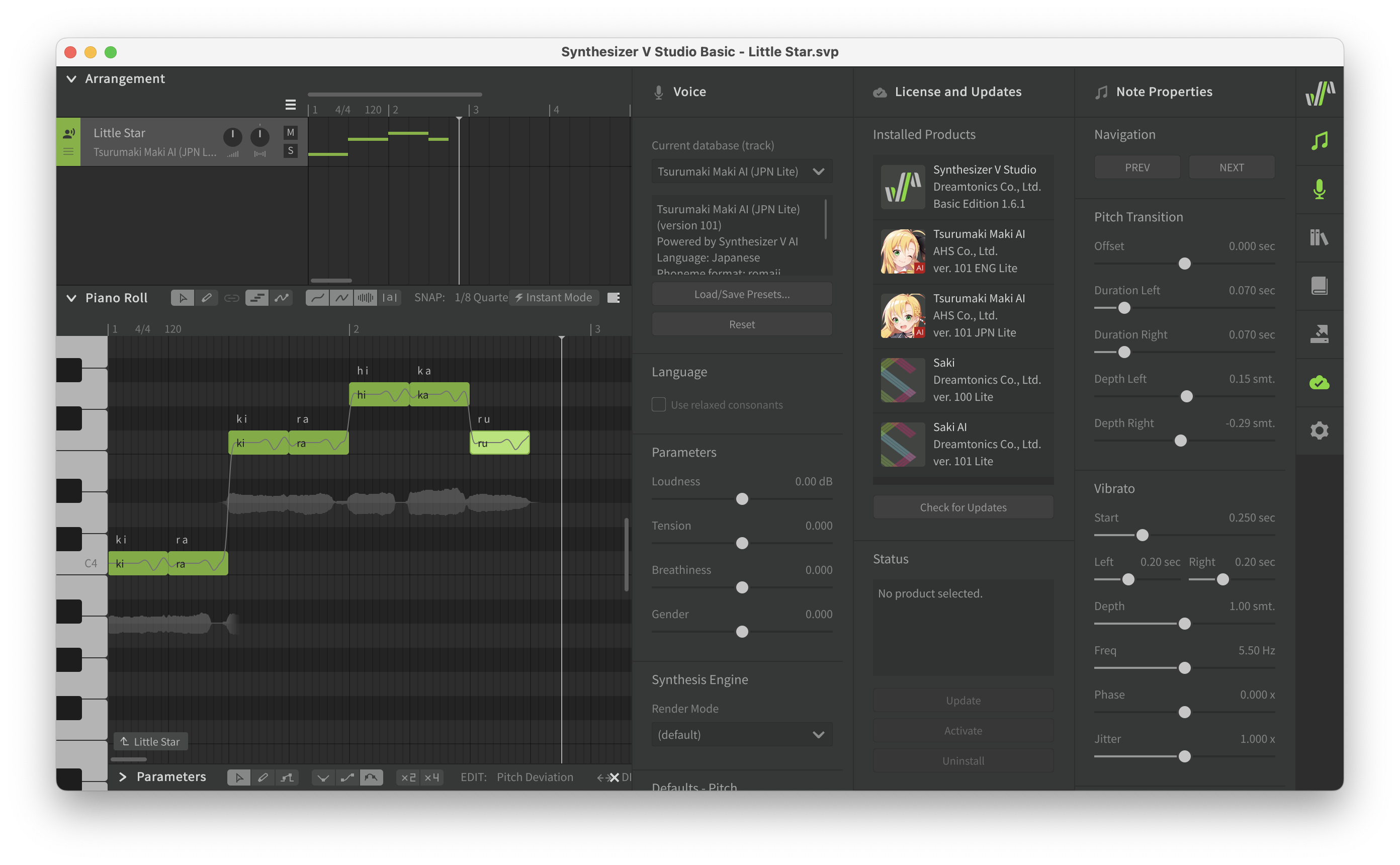
(以上截图来自 Synthesizer V Studio Basic, 歌曲是日语版的小星星, 刚学, 没有调教. )

某种程度上来说, 上面的操作相当于是在时间上将一段音频切做臊子细细剁碎了切开. 但是我~~中华小当家~~偏要换个方向”切” – 既然我们都知道了, 声音不过是一些简单振动的合成. 那么为什么不反过来思考 – 能否将声音分解成一些简单的振动呢?

没问题, 在很久之前, 一位叫做傅里叶的先生就说了: 能够将满足一定条件的函数表示成三角函数的线性组合. (将函数置于以三角函数系为基的函数空间).

就像是这个

(图片来源于维基百科)

于是我们可以将振动的声音变换成频率的组合 – 就好像是那些学音乐的大佬, 能够通过听声音就知道乐谱一样 – 我们现在有了能够将声音变换到频率谱的一个理论工具了.

关于傅里叶(级数)

让我们来一点点的简单的数学脑筋急转弯: 一个向量空间里面的向量都是由向量空间中的基向量的线性组合形成的. 比如说在多项式空间中有这样的一个多项式: $f(x) = \sum_i a_i x^i$. 这样的一个多项式我们可以看作是由向量 $x^i$ 等线性组合形成的. 并且这样的向量在特定的点乘, 记作 $(a, b)$ 的定义下: 比如 $(f, g) = \int_a^b f(x) g(x) \mathrm{d}x$ 就是一个可行的例子.

(或者你也能够说这个就是一个映射, 一个从多项式空间映射函数空间的映射, 不过这个其实不必这么看, 直接将向量空间看作是一种以函数为点, 或者说以函数为基的空间的话我觉得也不是不行. )

那么关于傅里叶变换. 我们可以将傅里叶级数看作是由三角函数作为基底的函数空间中的向量. 即: $f(x) = \sum_{i = 0} a_i \sin i \pi x + b_i \cos i \pi x$. 而这样的函数空间同时也有一些特殊的性质, 比如正交性($(a_i \sin i \pi x + b_i \cos i \pi x, a_j \sin j \pi x + b_j \cos j \pi x) = \delta_{ij}$), 归一化等.

现在, 假如有一个函数位于这个三角函数空间中, 那么该如何计算得到函数的"坐标"呢? 类比一般的向量空间, 可能并不太方便, 但是因为三角函数空间是一个正交归一的向量空间. 于是我们就可以类比直角坐标系空间求向量空间的方法: $x = \sum_i (x,e_i) e_i$. 即通过分别计算函数空间中的向量在各个基底上的投影 -- 也就是对应的坐标空间的分量, 来计算函数在函数空间中的坐标表示.

哦哦, 看这个! 在空间中的一个向量通过知道在三个坐标轴上的投影就能够知道在三个坐标轴上的分量, 也就相当于知道了坐标.

(图片来源于维基百科)

现在, 我们就能够得到坐标分量了, 即: $\int_a^b f(x) \cos x \mathrm{d}x$ 以及 $\int_a^b f(x) \sin x \mathrm{d}x$. (其中的 $[a, b]$ 就是函数 $f(x)$ 的周期区间. )

当然, 数学上的那些严格定义便被略去了. 在历史上, 虽然傅里叶在 1822 年初版的著作热分析理论首次引入了这个定理. 但是严格的证明确在很久以后才出现.

(不得不说, 有时候物理学家用起数学来, 真的是十分的自信. 传说(来自物理研讨小组老师)物理学家往往默认所有的数学求和的极限都是可以交换的, 也就是所有函数都是连续的 -- 于是突然有一天, 一个理论的却有两个不同的结果, 最后终于发现, 其中有一个求和极限是不能够掉换顺序的. )

现在你已经了解了一点点的傅里叶级数了. (大概)

这样的需求也是非常显然的 – 如果我去学习乐器, 让我按照波形图来摇摆, 总觉得有点强人所难了, 而如果是照着乐谱(也就像是我们的频谱一样)来演奏, 那么至少会简单直观一些. 比如以下面这段声音为例:

钢琴谱

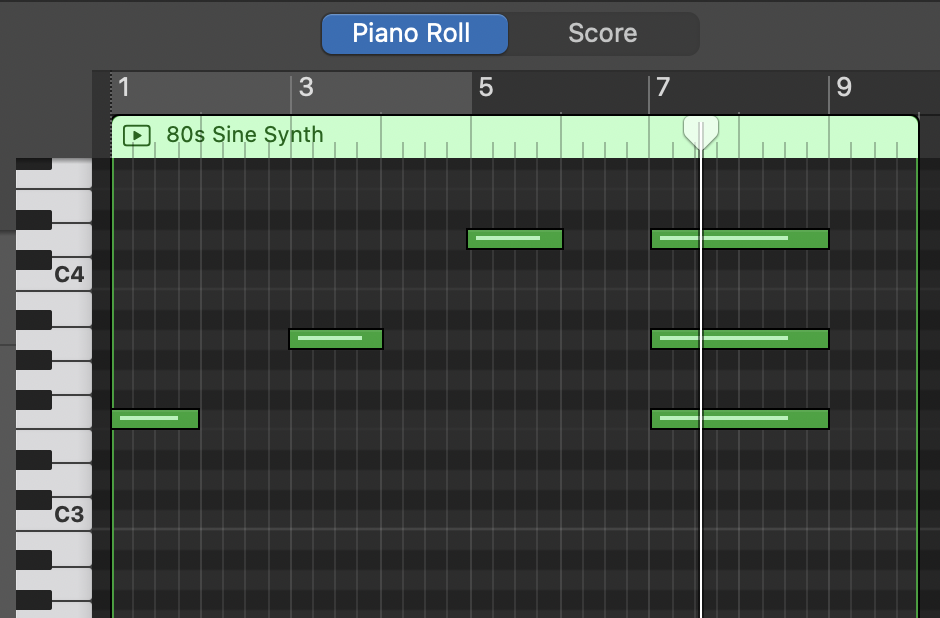
(图片来源于 GarageBand 截图, 音符是我瞎按的. )

并且不仅如此, 得知了频谱之后, 我们拥有了能够将声音分离的能力 – 譬如说, 像我这样的菜狗玩琴的时候可能会不小心按错了按键, 如果在波形图中, 我们可能很难将声音分离去除, 但是如果在频率谱上绘制, 擦除, 倒也不见得那么麻烦了.

钢琴谱的频谱

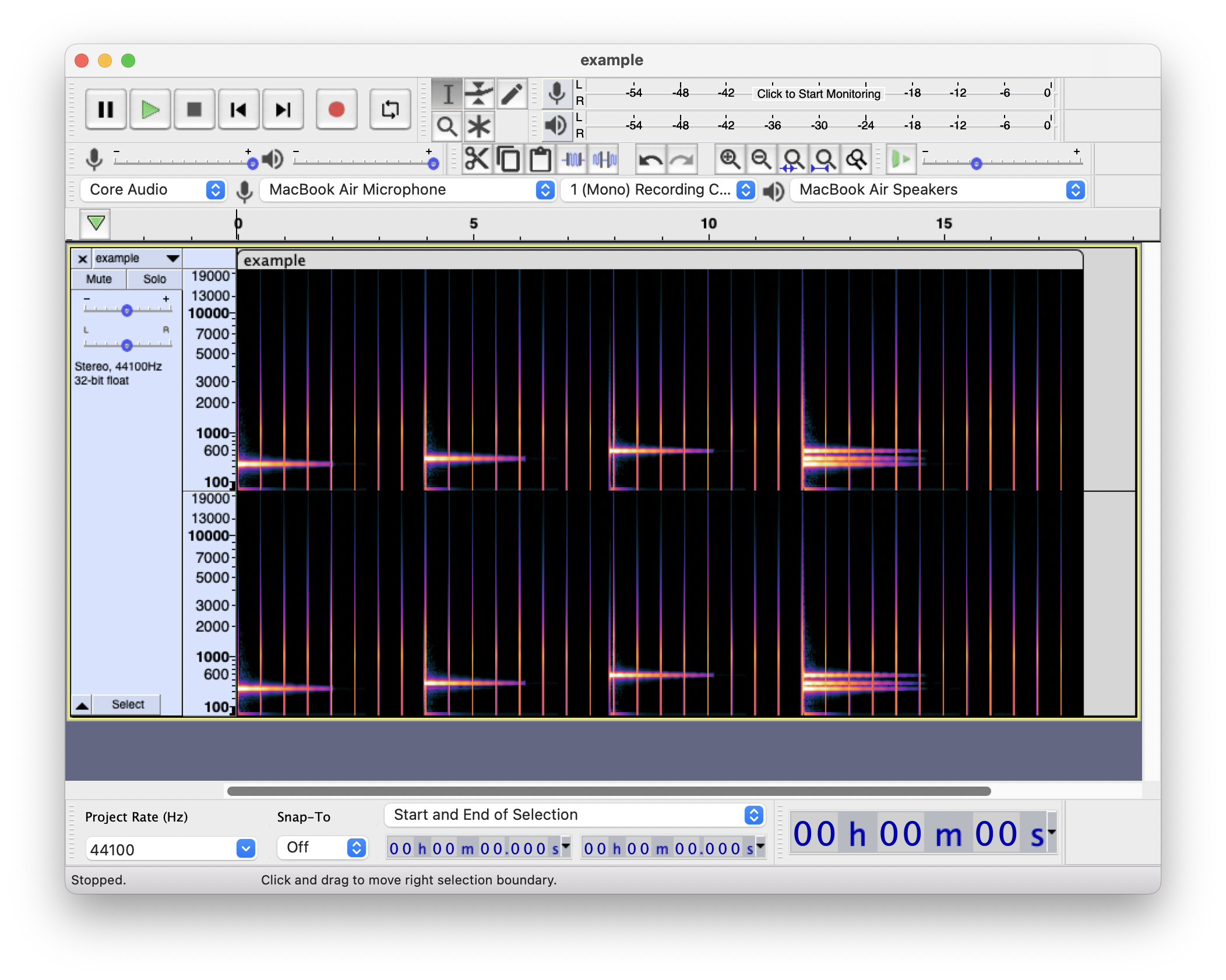
(图片来源于 Audacity, 是上面的乐谱的频谱. 可以在频谱中看到音符对应的频率分布. 不过其中的非常的长的纵向细线是节拍器的声音. )

比如在上面的图中, 我们就能够像在 GarageBand 软件中编写乐谱一样”方便”地处理声音 – 比如说想要修改和弦的种类, 在 GarageBand 软件中, 只需要移动一下音符, 但在波形图中, 则不会很方便, 而频谱图中, 我们只需要”擦除”对应频率的声音, 然后”画出”对应频率的新的音符即可.

而对五音不全的我来说, 我也拥有了能够拥有从音乐中分辨音符的能力了 – 类似的, 我们也能够通过类似的方式来分辨声音等其他数据的信息, 也就是说, 可以实现语音识别等高级的操作了. 不过这个也算是后话了. 按下不表.

(注: 其实并没有我说得那么美好就是了, 因为前面说了, 声音也并不一定是纯的, 所以要从一段复杂的声音中删除一些很复杂的声音可能并没有那么简单… 不过针对波形来进行处理也不是做不到. )

如何针对波形来处理声音

首先我们不妨假想这么样的一个东西: 频率越高的声音越容易(或者越不容易)通过通过. 于是将信号施加在这个东西上面, 频率高的信号就会被放行(或者阻拦). 于是我们就得到了能够过滤相应频率声音的装置了.

(虽然看起来好像还是根据频率来处理的. )

那么在现实中又是如何呢? 众所周知, 电容据有隔直通交的特性, 于是我们就能够利用这个特性和分压器的形式来制作相应的器件.

譬如将一个电容和一个电阻串联在一起, 那么这个电容(阻抗: $\tilde{Z}_C = \frac{1}{i \omega C}$)分到的电压为 $\tilde{U}_C = \frac{\tilde{Z}_C}{\tilde{Z}_R + \tilde{Z}_C} \tilde{U} = \frac{1}{i \omega R C + 1} \tilde{U}$. 于是不难发现, 当角频率越快, 电容分到的电压越小而电阻分到的电压也就越高 -- 于是, 如果我们将负载接在电阻两端, 就能够得到一个能够得到高频率信号的装置了.

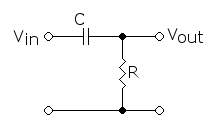
(图片来源于维基百科, 具体的关于高通滤波器, 低通滤波器和陷波等的电路设计, 可以参考任何一本电子学教材. )

具体一点的例子则是: 以上面的那段和弦为例, 我将和弦的一部分声音(600Hz)附近的音量通过类似于滤波器一样的东西去除掉:

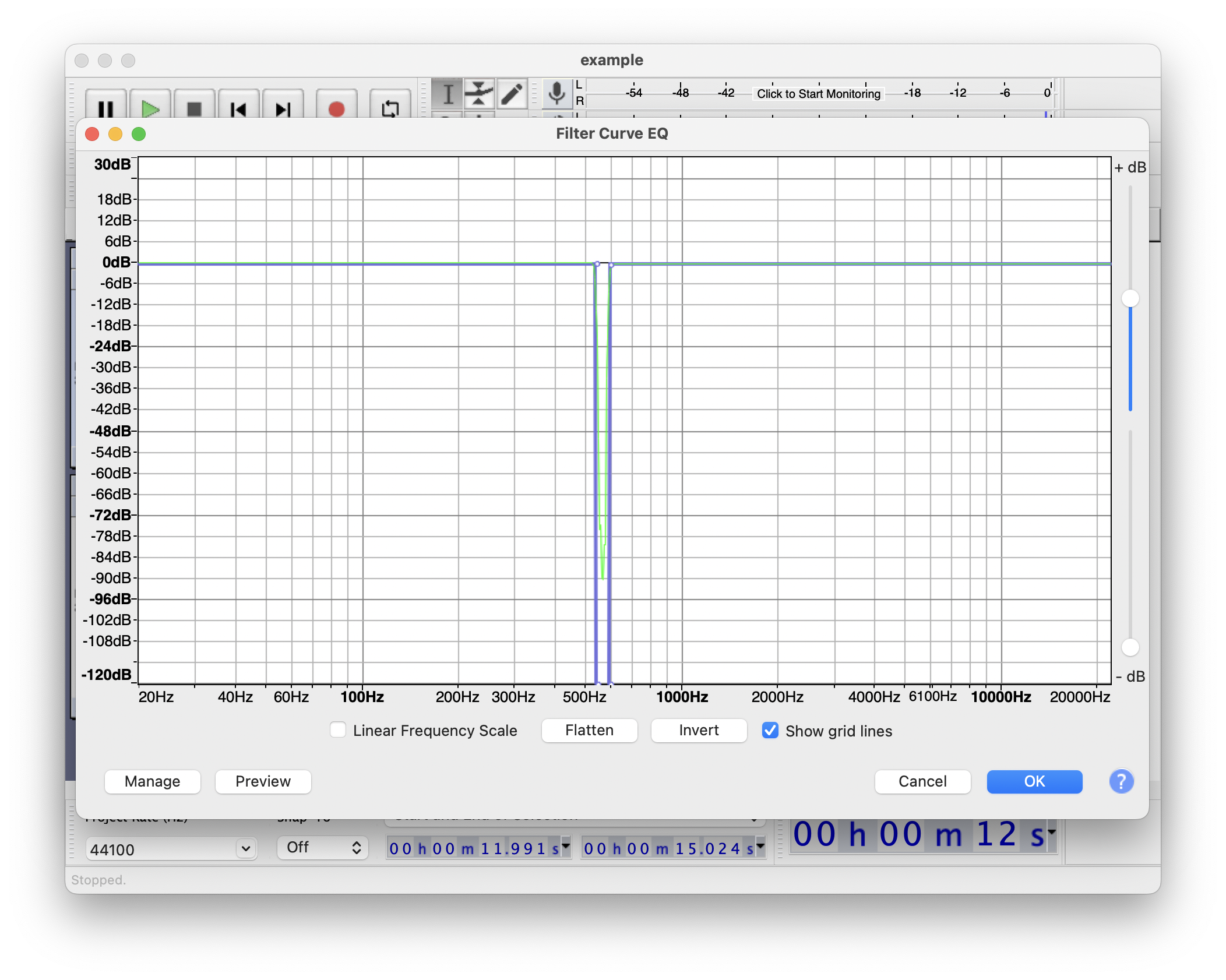
这就是一个类似于滤波器的东西, 在软件里面的名字叫做Filter Curve EQ, 用处是可以根据不同频率来确定对相应频率声音音量的增加或者减少.

去除后的效果如下:

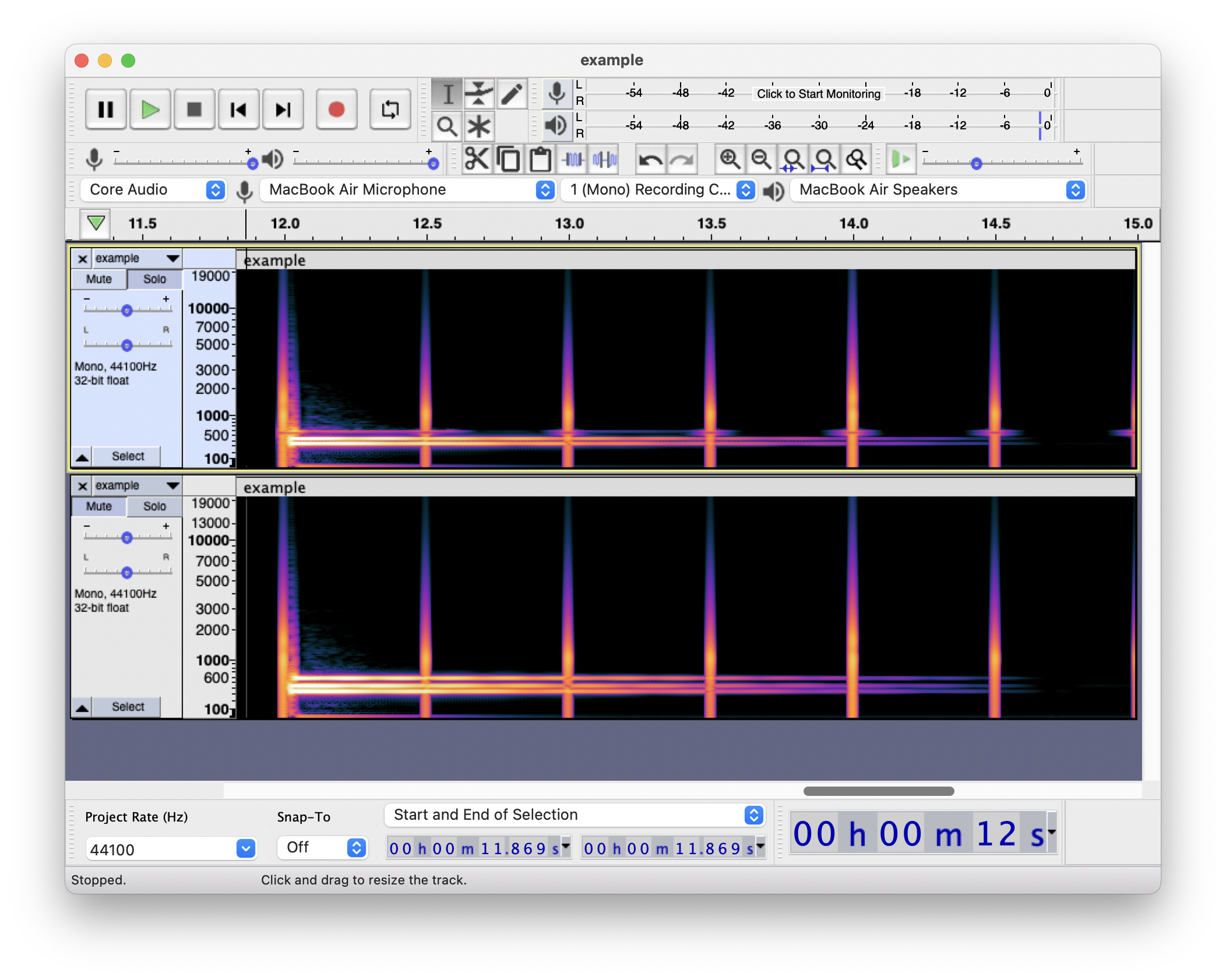
为了体现去除前后的对比, 我将原本的双声道拆分成了单声道 -- 一个对照组和一个实验组. 可以明显的看到, 对应 600Hz 的那条声音的亮度变暗了.

观察去后的结果, 可以明显看到 600Hz 附近的那条声音的亮度黯淡了下来吧?

没有去除的声音:

去除后的声音:

如果仔细听的话, 可以发现和弦中的高音部分没了(因为被过滤掉了). 而一般来说, 常见的去除一定频率声音的情境往往是环境中有些许低频噪音, 通过过滤相应的噪音, 就可以达到部分音频降噪的功能. (注: 这样的降噪和现在的降噪耳机的原理并不是一样的. )

当然, 傅里叶变换也绝不仅仅只能够在音乐中有所应用. 正如上面所见, 傅里叶变换让我们能够看到频率 – 这个对应声音特征值的量. 于是我们就能够抓住声音的特征来研究问题. 类似的, 除了声音信号, 我们还能够将傅里叶变换拓展到任意类型的信号上 – 譬如图像处理 (光的信号的处理, 可以参考知乎), 又譬如用于信号处理等方面. 不过这样的应用可能有些超出讨论的范围了.

关于傅里叶变换

在傅里叶级数的基础上, 数学家甚至还能够将变换推广到连续的形式:

$\mathcal{L}: \mathbb{R} \rightarrow \mathbb{C}, f(x) \mapsto \hat{f}(\xi) = \int_{-\infty}^{\infty} f(x) e^{-2\pi i x \xi} \mathrm{d}x$

啊, 这个是不是有点复杂? 一串的数学公式, 那么它们的物理意义呢?

首先来看这样的一个东西: $e^{i x}$, 这样的一个函数就像是三角函数一样据有周期性. 并且我们还能够通过最美丽的欧拉公式来知道: $e^{i x} = \cos x + i \sin x$.

于是和原本的傅里叶级数类比, 不难发现, 上面的 $\int_{-\infty}^{\infty} f(x) e^{-2\pi i x \xi} \mathrm{d}x$ 这一项与 $\int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \sin 2 \pi \xi x$ 是有着对应关系的. 于是我们可以说, $\xi$ 对应的就是频率项. 即 $\mathcal{L}$ 变换中将原函数映射到频率空间后所对应的频率上的强度.

于是在物理上, 不妨就可以将这样的变换看作为是一种特殊的投影变换, 将声音投影到一张"连续"的乐谱上了.

当然也有逆变换: $\mathcal{L}^{-1} : \int_{-\infty}^{\infty}\hat{f}(\xi) e^{2\pi i \xi x} \mathrm{d}\xi$, 相当于是在频率空间再投影回原函数空间去了.

但是连续的形式虽然很好, 但是不方便计算机去计算 -- 毕竟(目前的)计算机都是通过离散的数字信号来进行逻辑运算的产物, 所以就有智慧的前人利用巧妙的数学工具来解决这样的问题.

这样的问题叫做离散傅里叶变换 (DFT) 及其逆变换的方法. (来源).

DFT

前面的连续型的傅里叶变换想必已经不是一个问题了(狗头). 那么稍微复习一下便是: $\hat{f}(\xi) = \int_{-T/2}{T/2} f(x) e^{2 \pi i \xi x} \mathrm{d}x$.

学过一点点微积分的肯定知道一个叫做黎曼求和的东西, 我在这里将它写下: (其实就算没有学过, 也没有关系, 我在下面也同时会给出一个非常不严谨的推导. )

$$\begin{array}{llll} & \frac{1}{T}\int_{-T/2}^{T/2} f(x) e^{- 2 \pi i \xi x} \mathrm{d}x & = & \frac{1}{T}\sum \int_{a_k}^{b_k} f(x) e^{- 2 \pi i \xi x}\mathrm{d}x \\ = & \frac{1}{T}\lim_{\vert a_i - b_i \vert \rightarrow 0} \sum f(\eta_k) e^{- 2 \pi i \xi \eta_k} (b_k - a_k),\ \eta_k \in (a_k, b_k) & & \\ = & \frac{1}{T}\sum_{k = 0}^{k < N} f(\eta_k) e^{- 2 \pi i \xi \eta_k} \frac{T}{N} & & \eta_k = \frac{2k - N}{2N} T, \lim N \rightarrow \infty \end{array}$$

于是我们就能够说, 假如我们允许一定精度误差的情况下, 我们可以在有限的 $N$ 来计算原本连续的傅里叶变换 -- 也就有了下面这个"简单"的变换公式: $\hat{x}(\omega_{= 2 \pi \frac{k}{N}}) = \sum_{k = 0}^{k < N} x(k) e^{- i \omega}$.

于是可以写出一个简单的计算程序:

# expi(theta)
# return $e^{i \theta}$
def expi(x)
  Complex.polar(1, x)
end

# dft(input)
# return $_k = \sum_n x_n e^{-i \frac{2\pi}{nn} k n}$
def dft(x)
  nn = x.length
  (0...nn).to_a.map do |k| # compute x_k
    # $\sum_n x_n e^{-i \frac{2\pi}{nn} k n}$
    (0...nn).to_a.map { |n| x[n] * expi(-2 * Math::PI * k * n / nn) }.sum
  end
end

# dfti(spec) inverse dft
# return $_n = \frac{1}{N} \sum_k x[k] e^{i \frac{2\pi}{N} n k}$
def dfti(x)
  nn = x.length
  (0...nn).to_a.map do |n|
    (0...nn).to_a.map { |k| x[k] * expi(2 * Math::PI * k * n / nn) / nn }.sum
  end
end

来点例子

如果我们现在有一个波形数据: $a_{\mathrm{data}} = a_1 \sin 2 \pi f_1 t) + a_2 \sin (2 \pi f_2 t) + \cdots$.

# input syntax: [[f_0, a_0], [f_1, a_1], ...]
def make_samples(data, n)
  (0...n).map do |t|
    data.map { |f, a| a * Math.sin(2 * Math::PI * f * t / n) }.sum
  end
end

samples = make_samples([
  [2, 3], [6, 9], [10, 1]
], 128)

然后将这个样本数据进行傅里叶变换:

		
# make spec of input data
# output: spec[frequency]
def make_spec(data)
  dtf(data).map{ |i| i.abs / data.length }
end

spec = make_spec(samples)

# output spec
def output_spec(spec, range = nil)
  puts (range || (0...spec.size)).map { |f| "#{f} Hz: #{'#' * spec[f].to_i } #{'%.3f' % spec[f] if spec[f] > 0.5}" }.join("\n")
end

可以看出: 在输出的频谱上, 确实反应了我们生成时的波形数据和信息.

> output_spec(spec, 0..20)
0 Hz:  
1 Hz:  
2 Hz: ### 3.000
3 Hz:  
4 Hz:  
5 Hz:  
6 Hz: ######## 9.000
7 Hz:  
8 Hz:  
9 Hz:  
10 Hz: # 1.000
11 Hz:  
12 Hz:  
13 Hz:  
14 Hz:  
15 Hz:  
16 Hz:  
17 Hz:  
18 Hz:  
19 Hz:  
20 Hz:

上面的代码在误差范围内可以认为是一个比较合理的算法了... (大概吧)

关于 DFT 的栅栏效应

上面的公式中, 用到的 $N$ 是有上限的: 如果信息点只有 $N$ 个, 那么特征点最多也只能选择 $N$ 个. 这就好像是在有限的 $N$ 个特征点上观察 -- 就像是从栅栏的缝隙中观察景色 -- 观察到的信息的特征是有限的, 也就是说, 难以了解到更多频率的信息. 所以为了能够观察到更多的信息, 需要将原来的信号进行拓宽处理, 来获得更多的信息. (来源: 维基百科)

正如上面的公式 $\hat{x}(\omega_{= 2 \pi \frac{k}{N}}) = \sum_{k = 0}^{k < N} x(k) e^{i \omega}$ 所见, 当 $N$ 不够大的时候, $\omega$ 的取值也是有限制的.

所以为了解决这个问题, 一个简单的想法就是在后面加入空的采样点(值为零的点), 最终拓展到 $M$ 个采样点. 于是我们就能够得到关于新的频率的信息了.

但是需要注意的是, 这样的操作并不会提高变换的频谱分辨率 $\frac{2 \pi}{N}$, 因为 $\frac{2\pi}{M}$ 的分辨率仅仅只有计算上的意义而已. 想要真正提高, 可能只有通过提高声音的采样频率才行吧.

但是, 对于 DFT, 即离散傅里叶变换来说, 它的计算太过复杂可能并不适合计算机来处理. (因为太慢了. ) 所以为了加速DFT, 人们开始追求"快速傅里叶变换", 即 FFT.

FFT 的一些简单的实现 (来源: 算法导论)

既然 DFT 的速度不够快, 那么一个简单的想法就是如何加速计算. 注意到在 DFT 的计算中, 有一个函数被频繁地使用 expi, 即计算 $e^{i \pi x k}$ 的过程被反复地使用.

但是如果换一种观点, 不难发现 $\omega_{= e^{i \pi x k}}^{x} = 1$ 恰好是单位根. 而单位根有一些性质可以帮助我们简化计算过程. 譬如 $1$ 的 $n$ 次单位根 $\omega_n^k = e^{i k / n}$, 我们可以发现:

$$\begin{array}{llll} & \omega_{d n}^{d k} & = & \omega_n^k\\\Rightarrow & \omega_n^{n/2} & = & \omega_2 = -1\\\Rightarrow & (\omega_n^{k + n/2})^2 & = & (\omega_n^k)^2\end{array}$$

于是, 我们就能够利用这个方法来设计一种 "分治算法" 来加速傅里叶变换. 思路是这样的: 既然单位根的分布是关于 $x$ 轴对称的($\omega_n^{k + n/2} = -\omega_n^k$), 那么就可以利用这个对称的性质来减少计算.

譬如说, 如果我们想要计算 $\sum a_i \omega_{[n]}^i$. 那么一个简单的想法就是分别计算奇数和偶数 -- 因为:

$$\begin{array}{llll}A_{\mathrm{odd}} & = & \omega & (a_1 + a_3 \omega + \cdots + a_{n-1} \omega^{n / 2 - 1})\\A_{\mathrm{even}} & = & & a_0 + a_2 \omega + \cdots + a_{n-2} \omega^{n / 2 - 1} \end{array}$$

于是只需要计算 $\omega^0, \omega^1, \cdots, \omega^{n/2 - 1}$ 所分别对应的系数即可. 用数学公式来表示就是: $$\begin{array}{lll}y_k & = & A_{\mathrm{even}}(k) + \omega_n^k A_{\mathrm{odd}}(k)\\y_{k+\frac{n}{2}} & = & A_{\mathrm{even}}(k) - \omega_n^k A_{\mathrm{odd}}(k)\end{array}$$ 而在其中计算对应的系数的时候, 又能够再一次递归的利用相通的方法来计算, 即对 $a_1, a_3, \cdots, a_{n-1}$ 的计算再一次地折半.

于是代码如下:

# FFT
# recursive_fft(input)
def recursive_fft(a)
  n = a.length # n should be the power of 2
  return a if n == 1
  w_n = expi(2 * Math::PI / n)
  w = 1
  y_even = recursive_fft(a.each_slice(2).map { |n| n.last })
  y_odd = recursive_fft(a.each_slice(2).map { |n| n.first })
  y = []
  (0...(n / 2)).each do |k|
    y[k] = y_even[k] + w * y_odd[k]
    y[k + n / 2] = y_even[k] - w * y_odd[k]
    w = w * w_n
    end
  return y
end

# recursive_fft([1, 2, 3, 4])
# => [(4.0+0.0i), (0.9999999999999999+2.7755575615628914e-16i), (2.0+1.1102230246251565e-16i), (3.0-2.7755575615628914e-16i)]

虽然注意到其中有一个小小的时间唯一, 但是在一定程度上来说是可以接受的. 不过这里有一个类似 Ruby 写的结果: 链接 .

当然, 如果你不喜欢递归形式的写法的话, 可以考虑使用迭代形式的写法, 利用所谓的蝴蝶操作来加速计算等等. 不过这个就有些超出篇幅了. 所以就先放放吧?

注: FFT 不是一种算法, 而是一类算法的总称. 在我查算法书的时候(我没学过OI, 我就是个臭搞物理的. ), 其中有很多的 FFT 算法实现, 比如 FFTW 和 FFTE 这两个, 名字比较好玩, 分别是"西方最快的快速傅里叶变换"(Fast Fourier Transform of West), 以及"东方最快的快速傅里叶变换"(Fast Fourier Transform of East). 这取名字的方式真的很好玩. 不过可惜的是, 这个东方并不是指中国, 而是日本... 任重道远了属于是. 当然, 这两个算法是可以用于多维的傅里叶变换的.

并且我们还要面对一个简单的小小问题: 一段声音, 如果要进行变换的话 -- 就可能须要一个非常巨大的 $N$ 的取样点. 这样的计算可能是非常头疼和艰难的一个问题. 那么一个直接的想法就是: 为什么不把一段声音切碎了, 变成一段一段小的声音片段来减少 $N$ 的数量. 这样的想法可以叫做小窗傅里叶变换.

(并且这样的想法其实还有一个好处: 还能够知道频率在时间上的分布. )

那么为什么不来点实操?

于是我们不妨看看一段声音的频谱:

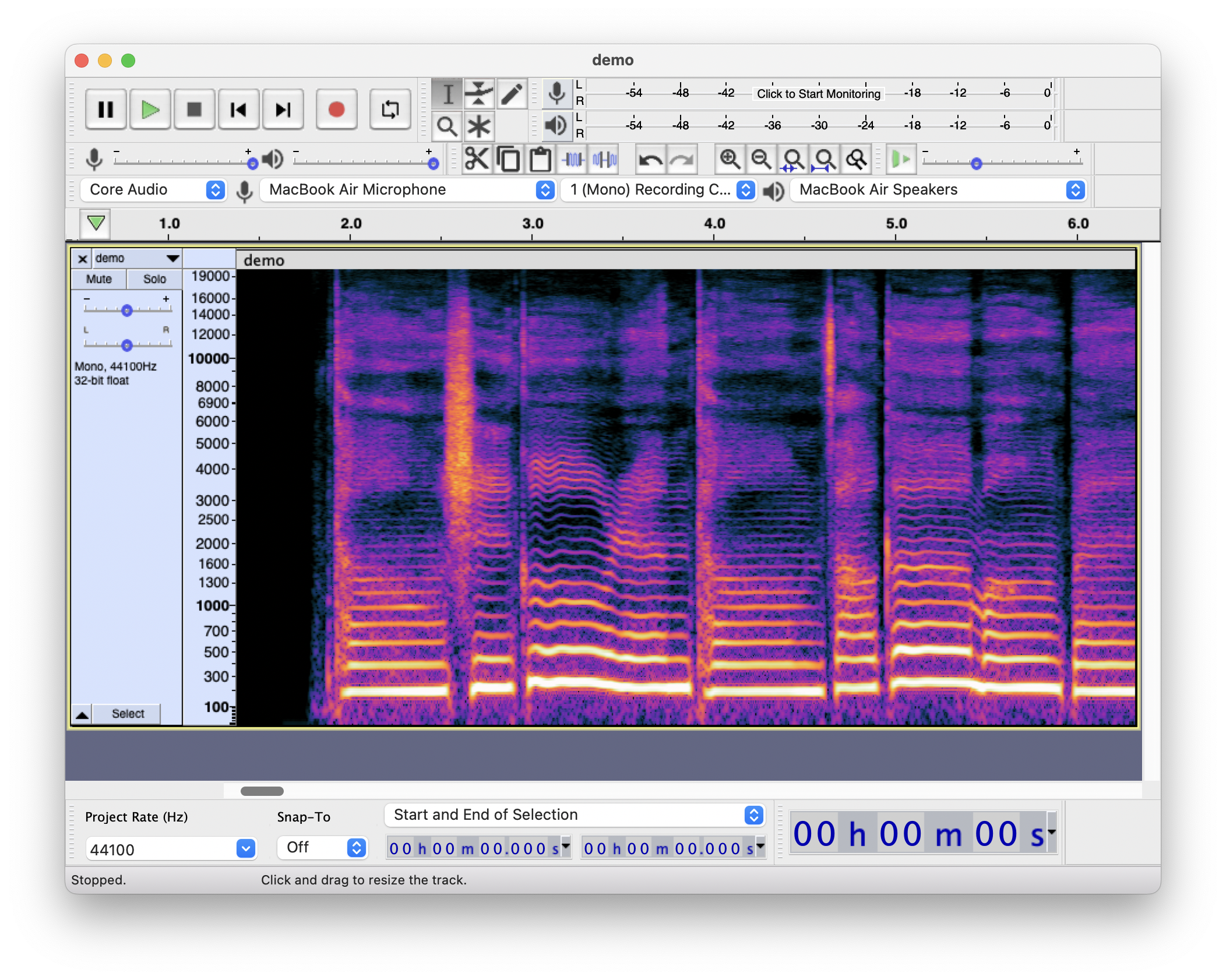
(上面的图片例子来自于 Audacity 的频谱查看功能. 使用的音频文件来自于 Synthesizer V Basic 中 Aiko 的声源合成的音频. 歌曲的原曲为似是故人来. )

观察图中的频谱图, 横轴为时间分部, 纵轴为频率分布, 在一个时间点上, 亮度越高的点的振动幅度(强度, 或者说, 对应的简谐振动分量的幅度)越大. 一个简单的类比就好像是用亮度来表现按下对应频率按键的力度, 于是一首歌曲就是像这样被写在”频谱”之上了.

正如前面所见到的钢琴乐谱和频谱之间存在的对应关系一样, 我们为何不可以换一种思路: 将频谱和钢琴乐谱之间进行一个”映射”, 然后让钢琴来唱歌呢?

太妙了, 这有什么理由不去试一试呢? 我们只需要将一段声音通过傅里叶变换变成频谱, 然后将频谱和钢琴的频谱对应在一起, 于是我们就能够得到用钢琴来”唱”的歌了:

原声:

(使用 Synthesizer V Studio Basic 生成的人声. )

使用 Garageband 中 80’s Sine Synth 音色 “说” 的声音: (强烈建议先听过一部分的原曲之后再听下面这段声音… )

(点击图片可以下载 midi 格式文件, 可以自己换音色. )

对于上面的一些解释

怎么做到的?

原理其实比较简单: 通过傅里叶变换得到声音的频谱, 然后将该频谱和 midi 的频谱映射在一起. 于是就得到了上面图中的 "乐谱" 了, 即能够让乐器说话了.

需要注意的是, midi 的频谱并不是像正常声音一样的连续分步的频谱, 而是间断的不连续的分布的. (如果还有兴趣了解的话, 可以考虑了解一下十二平均律, 一种用来计算每个音之间的音高, 即频率关系的规则. ) 于是如果遇到频谱中的声音落在两个音之间, 就需要进行一定的取舍了. 并且, 并不是所有出现在频谱中的频率都能够被映射到 midi 频谱上, 一些振幅太微弱的频率的声音, 我们也应该将其忽略不计 -- 毕竟小量近似是物理中常见的一个操作嘛...

于是我们就得到了音乐的"乐谱". 当然, 因为上面的操作中有太多的近似, 约化和省略, 我们自然很难得到和原来声音一模一样的声音了.

那么你讲的这些是真的么?

哦, 我懂了. 论文要注重一个可复现性, 哪怕是科普文章也要如此, 不然不就是造假和扯淡了么. 所以我应该给出一些可以复现的东西: MP3转MIDI.

上面那个网站就是我用来生成 midi 音频文件的工具了. ( 哈哈, 为什么不自己写? 因为太麻烦了. 虽然我也想, 但是读取文件和写入文件不是很会, 目前太菜, 以后没准可以. 又是一个梦里啥都有的发言... )

至于其他的配图和音频, 我都在图片下方和音频附近标注了来源和生成. 有兴趣的可以尝试复现一下.

横切还是竖切, 能切开的都是好瓜(bushi)

既然已经有了傅里叶变换这把快刀, 再回过头去看原本的合音, 切音, 注音, 没准可能会有新的想法:

以合音为例, “之于” 二字被混在一起, 就像是 “之” 字的频率被部分地叠到了 “于” 字的频率之上 – 这不就像是一种傅里叶变换么?

同样的, 如果你想要让声音变调, 你也同样可以通过先施加变换, 然后将频谱上移, 于是你就唱出了很高的声调了. (这就像是在弹钢琴的时候, 把乐谱中的基准点上移一样. 大概)

或者说, 当我们想要把两端声音和谐地放在一起, 在简单的接头霸王式的操作没有一个很好的结果的时候, 我们也可以利用傅里叶变换来将两端音频相接的部分混合在一起, 达到一个比较 “自然” 的混音效果.

可以发现, 有了傅里叶变换, 我们就拥有了自由处理信号的能力. (其实傅里叶变换远不只于此, 不过这都是后话了. ) 有了这么强大的处理能力, 为什么不来… ?

后记

哦, 对了, 好像 7 月 12 日是中国歌姬洛天依发售的 10 周年. (Vocaloid 3 Library 洛天依 Vocaloid China Project 制作, 上海禾念开发发行于 2012 年 7 月 12 日. 来源).

虽然这个博客可能写完之后早就过去超级久了… (对不起, 我是一个懒惰的人, 不过也有一点点原因是因为我还要去学一点点新的东西. )

在这篇文章写得差不多的时候, 我突然看到了另外一篇文章, 或者倒不如说是一个项目. 感觉其中傅里叶变换的分析逻辑讲得还挺好. (我是用翻译软件看的, 目前还不能通读 – 没有这个耐心. ~~以后没准可以.~~ 梦里啥都行. ) 然后是一个视频… 嗯, 人家动画也做得比我好, 如此一比, 甚至感觉我输了的感觉.

哦, 关于文中使用的音频素材… 是不是有一个歌曲来着? 在这里:

(音频由 Synthesizer V Studio Basic 合成导出, 其中人声部分由 Aiko 声源制作, 伴奏由 Garageband 生成. 歌曲的原曲为似是故人来, 只做了前两个小节. 工程文件可以在这里下载. )

虽然总觉得有点不好, 声音还是有些不过自然, 作为第一个练手学习的项目而已… 不过我可以自豪地说, 这段音乐是没有任何真实歌手, 乐器参与的电子合成音乐了, 音源可能是真实的就是了…

啊, 小时候喜欢初音未来, 估计其中有很大的原因是在于我喜欢这种美妙的技术 – 立体投影技术, 电子人声合成技术…