你好, 小朋友, 请问你们知道降噪耳机吗?
About
先别问小朋友们知不知道, 总之先给我来张 Silence 卡, 对, 就是小樱那张.
和吃席坐小孩那桌相对的估计就是坐车和小孩一车吧. 而我的更离谱一些, 我是和一车小孩…
算了, 再多熬一会儿, 等我耳机充完电就好… 所以这篇文章只会是一个非常短小的科普文章.
逆转降噪耳机
大多数人可能会因为 “降噪耳机” 万分吸引人的名字而尝试入手, 然后在经历现实拷打之后大喊 “退钱!”. 但是我要说: “異議あり!”, 这可真的是误会它了.
当然, 为了防止刚来的吃瓜群众不太清楚事情的前因后果, 我们还是来简单地介绍一下案情吧:
被告降噪耳机以 “主动式” 降噪为主要卖点, 因为使用效果不佳而被我们的原告: Silence 库洛牌告上了我们的离谱法庭, 罪名为不能让自己在周围吵闹的环境里面安静地享受.
Silence: 这家伙虽然让我听不见了列车的嗡嗡声, 但是根本没有减少那帮小祖宗, 那帮扬声器们的声波武器!
很遗憾, 但是这就是事实, 主动式降噪耳机是有极限的. 所以我不做…
虽然能, 但是并不是万能, 也不是一定能. 这是因为…
你先别急, 听我狡辩
在这里我们先介绍两个简单的前置知识:
- 听到声音是空气的振动作用在鼓膜上, 使得神经细胞受到刺激最终在大脑得到信号的一个过程.
- 为了描述最简单的振动我们可以用 \(∑_{ω} A sin (ω t + \varphi_s) + B cos (ω t + \varphi_c)\), 也就是三角函数的形式来描述.
用一个最简单的振动 \(A sin ω t\) 来作为例子来解释上面的两个知识点:
- 在鼓膜 (耳朵) 边上的空气被压缩又膨胀, 就像是一根弹簧一样推动着鼓膜振动.
- 那么如果想要不听到声音, 只要在声音传播的这条路上埋伏起来偷袭就好了:
- 比如我们可以跑到真空中, 这个时候, 作为声音传播媒介的空气就消失了, 自然就一点也听不见了. 虽然这个时候你可能不太舒服, 但你就说这是不是消失了呢.
- 当然, 其他的一些操作可能过于地狱了一些, 不适合作为给小朋友的介绍, 还是算了. (比如由于鼓膜老化, 破裂等造成空气的振动无法转换为鼓膜的振动; 又或者是鼓膜到大脑的神经链路因为各种原因而损坏等等)
显然, 我们的目标应当是尽可能简单而无副作用地实现消除噪音的愿望, 毕竟这可不是啥猿猴之手呢. 所以最合理的做法就是切断在空气中的传播路径.
想要切断空气中的传播路径, 最简单的方法就是用手或者其他的东西将耳朵捂起来. 这就是 “被动式” 的降噪耳机的思路: 如何构造并选择更好的结构来使得外界的声音更难传入.
而相比被动式降噪耳机, 主动式降噪耳机的思路就是 \(A sin (ω t) + A sin (ω t + k π) = 0\). 用一个不太合理的图像来表示就是: 两个小孩在拉东西, 假如这两个小孩用的力气相等, 用的方向又时时刻刻相反, 嘿, 今天就是天皇老子驾到, 你也别想这东西能被拉动.
于是稍微复杂一些, 如果现在的振动模式变成了 \(A_1 sin (ω_1 t + \varphi_2) + A_2 sin (ω_2 t + \varphi_2)\), 那么如果想要消除 \(ω_2\) 频率的分量, 那么只需要引入一个新的振动 \(A_3 sin (ω_3 t + \varphi_3)\), 使得 \(A_2 = A_3, ω_2 = ω_3, |\varphi_2 - \varphi_3| = k π\), 于是合成的结果就是 \(A_1 sin (ω_1 t + \varphi_2)\).
那么能不能更加复杂一些呢? 如果现在的振动模式变成了:
\[∫_0^{∞} A(ω) sin(ω t + \varphi(ω)) \mathrm{d}ω\]
如果想要消除频率区间为 \([ω_1, ω_2]\) 的振动分量, 那么只需要添加如下的振动模式即可:
\[∫_{ω_1}^{ω_2} A(ω) sin(ω t + \varphi(ω) + π) \mathrm{d}ω\]
Silence: 那不是超级简单吗? 你这个骗子! 我现在外面这些声音, 可是一丁点都不想听见, 请将频率区间 \([0, ∞]\) 的都给我去掉!
你说的对, 但是降噪耳机是…
理论上是这样的, 但是上面只不过是降噪耳机原理中的冰山一角而已. 因为首先我们就要遇到的一个问题是: 我们周围的声音振动, 对我们来说, 更像是一个时间上连续变化的信息 \(A(t)\). 我们并不 (能直接) 知道它是由什么频率的什么分量组成的.
理论很美好, 现实很骨感, 首先, 为了能够得到量化可计算的 \(A(t)\), 我们需要一个麦克风. 而沉重的现实打击就已经从这里开始了:
- 正如人耳对过高频率和过低频率的声音并不敏感,
甚至会出现截止现象 (超声波和次声波听不见),
大多数麦克风对于不同频率的相应并不相同.
尽管我们可以通过标定输入测量一条频响曲线, 从而对不同频率给予一个修正系数.
关于修正系数的一个无关的例子
因为我也不是搞这个的, 所以没啥好的例子. 一个相近的例子为我在近代物理实验里面的滤波器的测量:
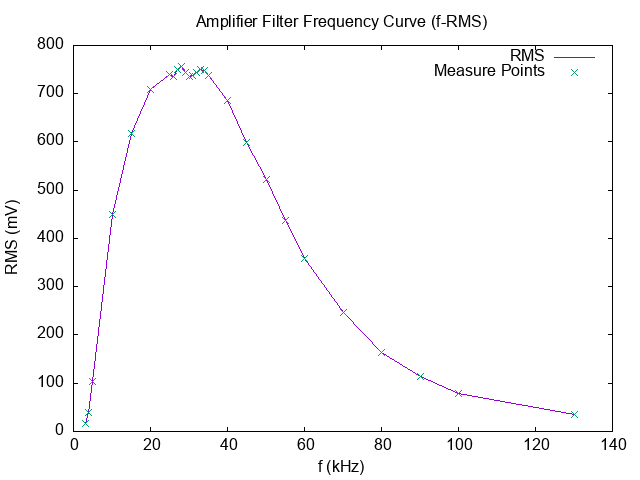
让我来解释一下这个图吧.
- 当时需要标定一下仪器 (滤波器), 然后就用一个标准输出 (函数发生器) 以相同幅度和不同频率作为输入, 用示波器测量输出, 得到了这张图片.
- 根据频响曲线, 就可以反推在某频率上测量的实际输入值, 也就是乘/除以一个增益系数.
- 梦里的滤波器应该是一个直上直下的平台, 除了边缘, 其他地方不是 0 就是 1.
显然, 我手上测的这个是个现实的滤波器.
那么滤波器和麦克风又有啥关系呢? 我觉得可以把麦克风看作是一种特殊的滤波器, 只不过理想的麦克风应该是一个平台无限宽, 高度恒为 1 的平台. 显然, 现实还是很骨感的.
并且这个频率相应的限制因素估计不仅仅是电子学的, 可能还有机械结构上的限制. 不过这个我就不太会了.
一个修正系数的直观例子如下: 假如输入信号为 \(100\), 经过麦克风拾取的强度为 \(99\), 那么就可以认为修正所需的系数为 \(\frac{100}{99} ≈ 1.0101\). 但是如果拾取的强度太弱, 譬如 \(100 → 0.5 ± 0.5\) 甚至更弱, 那么最终的结果就是, 在这里为了保证信号的正常, 必需做一个截断防止出现问题.
- 而在好不容易拿到声音信号 \(A(t)\) 之后, 一个更加麻烦的问题出现了,
我们好像还需要从中提取出频率 (空间) 的信息.
当然, 这个不会是本次的重点, 好奇的小朋友可以去看之前的文章: 舌头大姐了…, 一个剧透就是好用的傅里叶变换.
真正重点的是, 我们该如何使用傅里叶变换. 举个例子, 教科书中的傅里叶变换:
\[\mathcal{F}(f) = ∫_{\mathcal{D}} \frac{1}{2 π} f(x) e^{- i k x} \mathrm{d} x\]
其中 \(\mathcal{D}\) 为值域 (一般为 \((- ∞, + ∞)\), 也可对非无穷大值域做延拓). 但是这样就会要求知道整个值域的信息 – 这可是非常离谱的事情, 想要消除声音, 竟然要等到听完所有声音信息后才能消除…
这不就是小学生的选择性失聪嘛于是这个时候的一个妥协的方法就是只对一小部分进行傅里叶变换, 即把要消除的声音切做细细的一个个片段, 对每一部分进行傅里叶变换, 然后根据提取的频域信息去消除对应的小片段的声音.
当然, 这样的做法其实还需要一些小小的讨论, 只是在这里先跳过先.
- 那么理想的情况下, 只要令这个小片段的时间宽度尽可能的短,
那么降噪的实时性应该就会更好.
然而事实是, 我们还有需要妥协的问题: 假如选择的时间宽度 \(τ\) 过短, 因为采样率限制导致波形的分辨率不足而导致失真, 这样则太尴尬了.
关于分辨率的一些无关注记
说道分辨率就让我想到示波器, 测量的时候, 理应采样率应该是 \(× 10^3\) 倍于被采样的信号.
显然, 如果真的有这么强的示波器的话, 哪怕是一些原理看上去非常 low 的: 利用区间速度逼近瞬时速度的挡板法测斜坡上的小车速度, 也能够变得非常强, 比如在近物所的环形加速器上按了两个探测器来检测重离子经过 – 大概是 \(\mathrm{n}s\) 量级的一个分辨率 (具体我记不清楚了, 诶, 属于是听讲座不用心, 不过应该会更小一些).
- 并且时间宽度 \(τ\) 也应当和计算时间 \(τ_{\mathrm{c}}\) 相匹配, 尽管我不知道具体的实现方式应该是啥.
这里我提供一个非常简单的朴素想法: 认为在 \(t\) 周围 \(λ τ\) 的一个领域里面,
认为振动的模式是相似的, 于是可以认为, 若 \(τ_c < λ τ\), 那么就认为它还算是可以降噪吧.
于是这里就对计算时间和时间宽度之间加了一个限制, 想要消除更高频率的声音, 就应当让 \(τ\) 更小, 于是就变相要求 \(τ_{\mathrm{c}}\) 更小, 就要有更加快速的芯片 (估计可能会有更高的功率消耗, 使得电池电量减少, 毕竟我看我可怜的耳机从电池仓里出来都是红温的 (热的)…)
大概就这样吧, 一下车心情都好了, 也就不咋想吐槽了.