未若柳絮因风起
未若柳絮因风起
谢太傅寒雪日内集, 与儿女讲论文义. 俄而雪骤, 公欣然曰: “白雪纷纷何所似? “兄子胡儿曰: “撒盐空中差可拟.” 兄女曰: “未若柳絮因风起.” 公大笑乐. 即公大兄无奕女, 左将军王凝之妻也.
虽然如此, 但是在柳絮漫天飞舞, 钻进口鼻耳中的现在, 炎炎烈日照耀我的头顶, 体育课上除了躲在树荫下摆烂聊天, 鄙人实在是没有什么风雅的情操去思考什么”未若柳絮因风起”的高雅故事.

柳絮团
在空中飘飞的柳絮虽然给人一种雪花飘飞的美感, 但是气温实在是让人难以想到冬天的感觉. 所以蹭完饭后坐在草坪上双眼呆滞等待上课的我忽然发现了违和点: 好像有些柳絮有点大过头了.
先说说大部分的柳絮应该大概长什么样吧: (说起来, 俺是南方人, 却感觉自己完全没有见过柳絮, 估计都是被梅雨给封印了吧… )根据我的不完全观察, 大概就是在一撮毛毛里面有一个像种子一样的核心.

然而这些柳絮好像也知道单兵作战不太好, (让人吸进去多不舒服啊), 所以我看到了它们采取了集团冲锋的战术, 在地上卷起来了:

仔细观察, 我发现柳絮的形态并不是只有单个, 球状这样简单粗暴的分类:

尽管这些团状柳絮本来都应该是由简单的一小撮柳絮组成的, 但是这一大堆东西凑在一起却会有不同的表现形态. 真是不得不说: 好家伙, 哪里都有凝聚态?(众所周知, 一个粒子容易琢磨, 一堆粒子就难以琢磨了. 啊, 好像是筷子? )
来点理论
(下面的理论过程由我的热学老师林老师和物理学院群里的水怪启发, 在此表示感谢. )
一个柳絮在空中随风飘动, 在这个自由自在的空间里面, 我们不妨将其看作是一个特殊柳絮(粒子)扔到了一堆普通柳絮(粒子)里面. 其中:
- 假设所研究的特殊粒子平均移动\(\overline{\lambda}\)的路程后发生一次碰撞.
- 每次碰撞后有\(P\)的概率和其他粒子粘合在一起.
- 碰撞后认为原本的特殊粒子的相对移动不会发生变化.
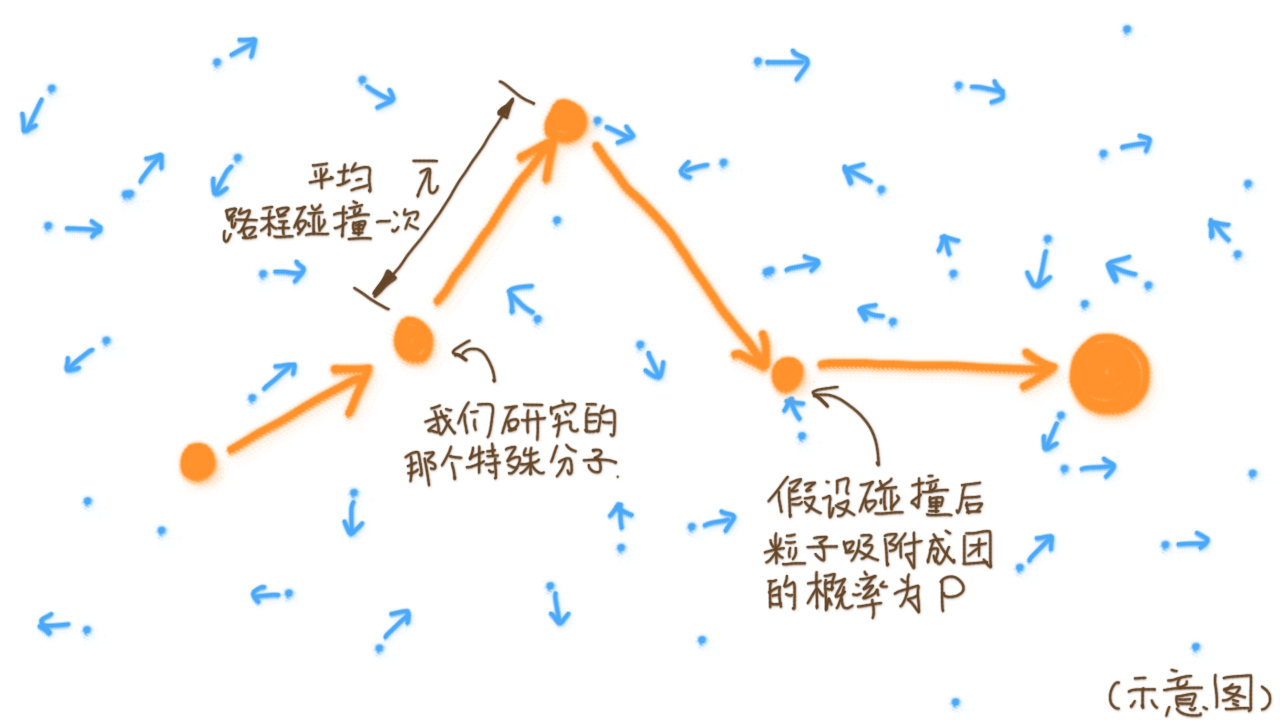
于是假设该粒子的速度是\(u\), 那么假如记每个小粒子的体积为\(V_0\), 那么碰撞后增加的体积为:
\[\Delta V = P n_{碰} V_0 = \frac{P u V_0 \Delta t}{\overline{\lambda}} \Rightarrow \frac{\mathrm{d}}{\mathrm{d}t} V = \frac{P u V_0}{\overline{\lambda}}\]一点点更加细致的描述
给我四个参数, 我能描述一只大象, 再给我一个参数, 我还能让它摇摇鼻子.
– 不知道该算是谁说的, 反正故事在这里.
上面的方程里面的参数稍微有那么点多. 而那么多参数的东西, 在理论学家的眼中则像是一只鵺一般, 高喊着: “这玩意有问题! “ 所以通过寻找参数之间的相互关系, 就能够将未知的参数(那些需要硬凑的参数)给减少:
(注: 下面的公式推导可以忽略不计, 我会在最后给出一个比较直观的解释. )
平均自由程
假如不发生多粒子碰撞, 只有两个粒子的碰撞, 那么碰撞的时候, 我们可以粗略地将其他粒子看作是静止的, 而我们的粒子相对它们以平均相对速度$\overline{u_r}$运动.
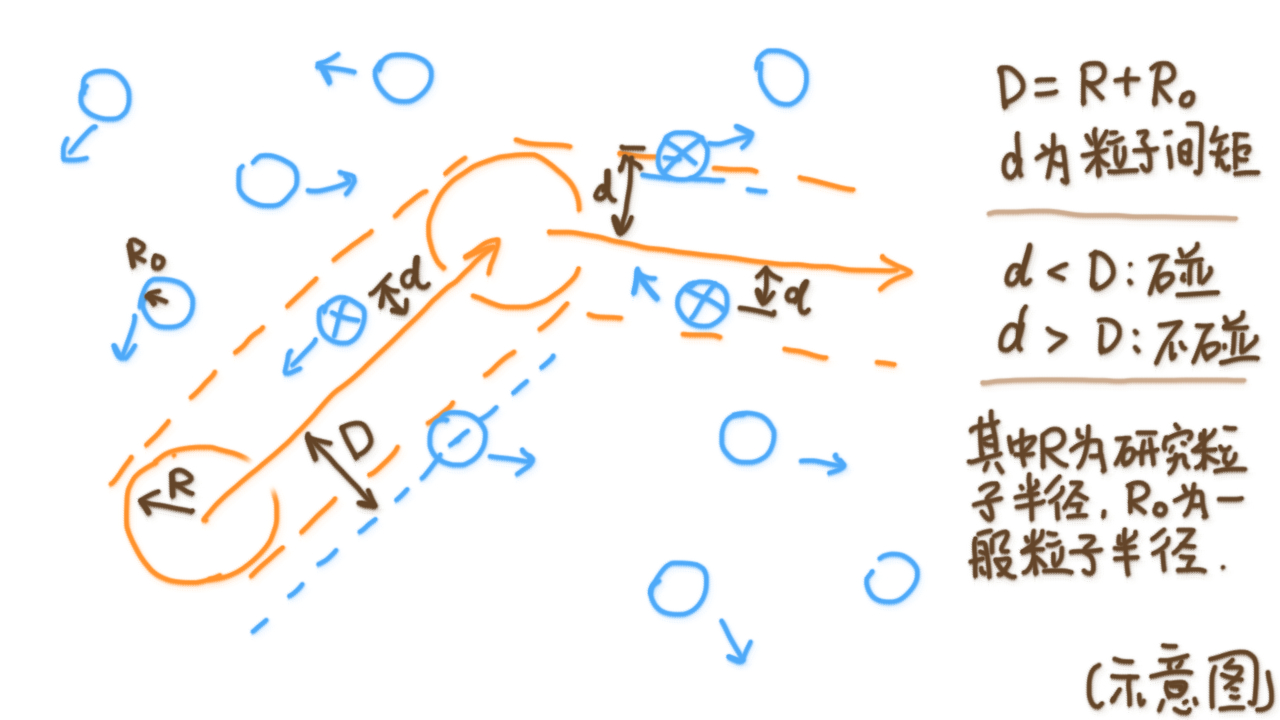
于是我们的粒子就像是穿行在一堆灰尘里面的扫地机器人, 那么扫到的空间的体积$V$就是碰撞面积$\pi D^2$和移动距离$\overline{u_r} \Delta t$的乘积了. 而在粒子数密度$n$(单位体积内有的粒子数量)的空间里面, 所收集到的平均粒子数量(也就是发生的碰撞的平均次数)即为$\overline{N} = n V = n \pi D^2 \overline{u_r} \Delta t$.
于是平均自由程(单位时间里面移动的平均距离)\(\overline{\lambda} = \overline{u} \Delta t / \overline{N} = \frac{\overline{u}}{\sqrt{2}n \pi D^2 \overline{u_r}}\).
这个时候, 虽然知道了平均自由程的关系, 却又引入了粒子间的相对速度$\overline{u_r}$的参数. 所以一个简单的想法就是如何通过平均速度来知道平均相对速度:
两个质点之间的平均相对速度
考虑两个质点之间的相互运动, 假设它们各自的速度(相对大气)分别是\(u_1\), \(u_2\).
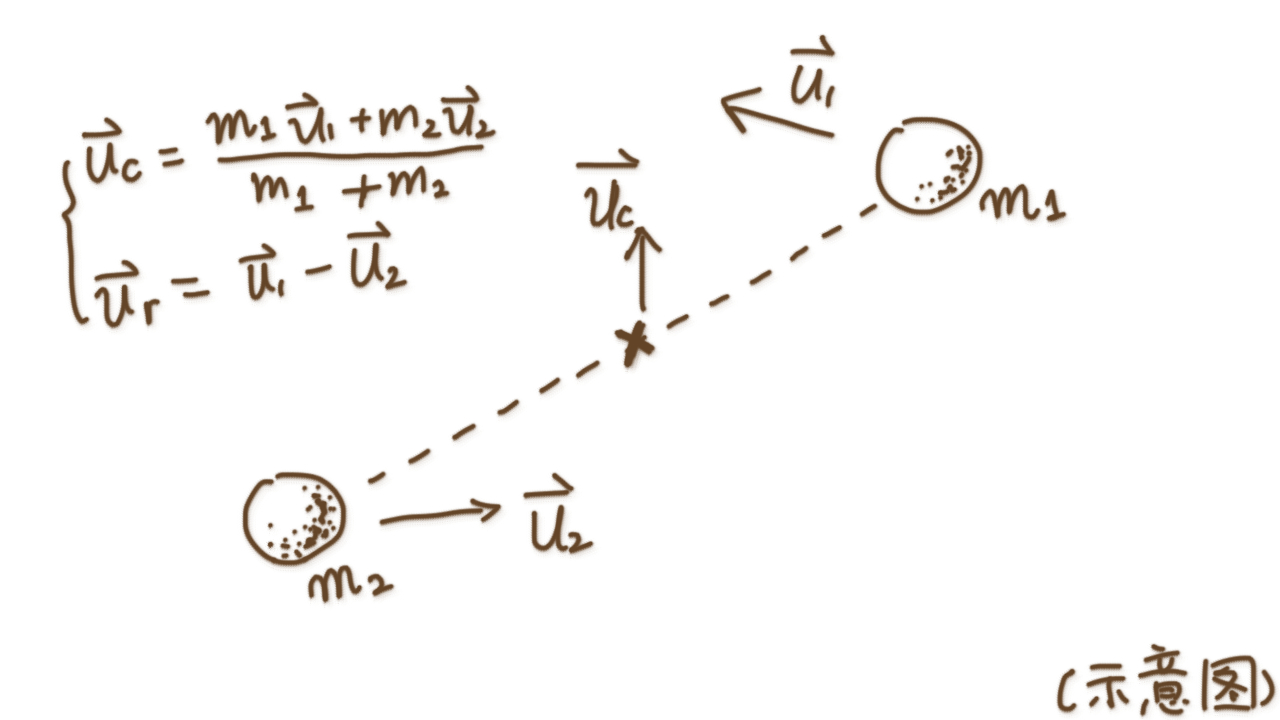
因为两个粒子碰撞是相对的碰撞, 所以需要得知两个质点之间的平均相对速度, 就能够了解碰撞的情况了\(\overline{u_r} = \int u_r f(u_r) \mathrm{d} u_r\).
而已知质心的速度\(u_c = \frac{m_1 u_1 + m_2 u_2}{m_1 + m_2}\). 在质心系上看, 两个的运动相对速度则是\(u_r = u_1 - u_2\). 因为这两个粒子是相对独立的, 也就是说, 它们的速率分布是相对独立事件, 即出现一个粒子的速率为\(u_1\), 另外一个粒子的速率为\(u_2\)的情况的概率为\(f(u_1) f(u_2) \mathrm{d}u_1 \mathrm{d}u_2\). 其中\(f(u)\)为麦克斯韦速率分布: \(\sqrt{\frac{m}{2\pi k_B T}} e^{-\frac{1}{k_B T} (\frac{1}{2} m u^2)}\).
于是用$u_c$和$u_r$表示$u_1$, $u_2$, 然后得到: \(f(u_1) f(u_2) \mathrm{d}u_1 \mathrm{d}u_2 \varpropto e^{\alpha ((m_1 + m_2) u_c^2 + m_r u_r^2)} \mathrm{d}\vec{u}_c \mathrm{d}\vec{u}_r\). 对$\vec{u}_c$积分, 然后将$\vec{u}_r$限制在径向. 最终可以得到速率分布为\(f(u_r) \mathrm{d}u_r = (\frac{\mu}{2\pi k_B T})^{3/2} 4\pi u_r^2 e^{-\frac{\mu u_r^2}{2 k_B T}} \mathrm{d} u_r\). (其中$\mu$为约化质量. )
经过积分\(\int u_r f(u_r) \mathrm{d}u_r\)可以得到$\overline{u_r} = \sqrt{\frac{8 k_B T}{\pi \mu}} = \sqrt{2} \overline{u}$, 其中$\overline{u}$为粒子相对大气的平均速度.
一个通俗的理解就是, (非相对论效应下)两个粒子的相对速度应该和粒子的速度是线性关系, 所以有$\overline{u_r} = \sqrt{2} \overline{u}$的关系, 这个$\sqrt{2}$就是一个系数.
整合一下
经过了上面的分析, 可以得到:
\[\frac{\mathrm{d}}{\mathrm{d}t} V = \sqrt{2} n \pi D^2 P V_0 \overline{u}\]对于体积$V = \frac{4\pi}{3} R^3$, 于是可以得到半径随时间变化的大概规律:
\[\frac{\mathrm{d}}{\mathrm{d}t} R \varpropto \frac{(R + R_0)^2}{R^2}\]然后计算的结果应该会像是这样的东西:
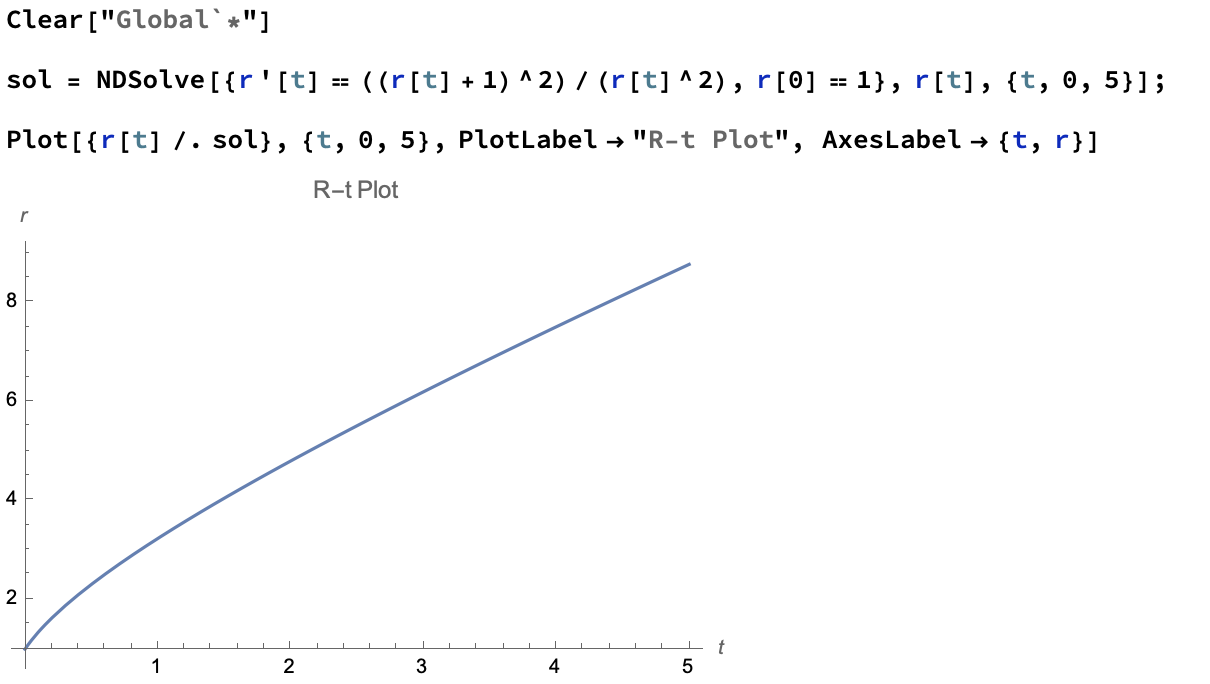
嗯, 这样的分析过程感觉还挺有意思的… 可以发现, 一开始半径增长的速度较快, 但是逐渐变慢, 最终趋于一个线性关系.
虽然实际情况是不是这样我就不知道了. 因为实验观测柳絮的变化我觉得还是困难了点. 但是可以制作这样的一个装置:
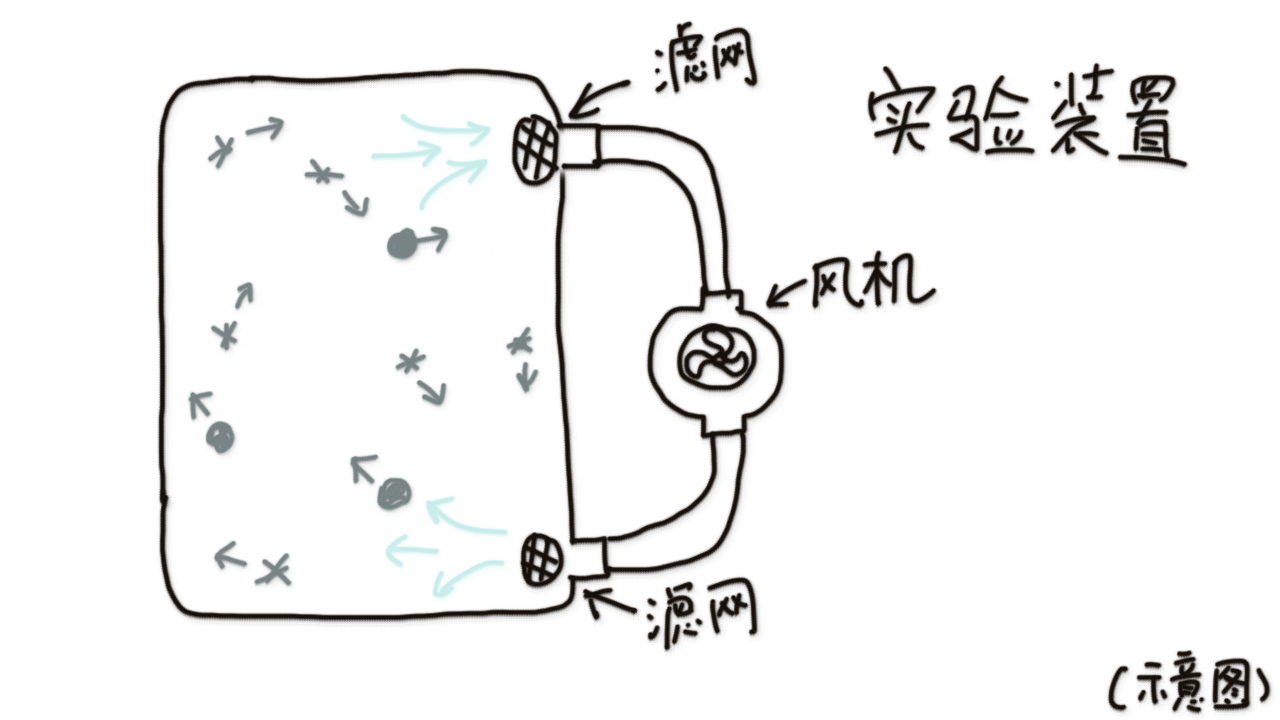
然后通过观测其中的絮状物的变化来进行实验验证.
柳絮: 嗯, 所以关我什么事?
有没有一种可能, 通过这样的分析过程, 可以用来描述细胞在最初的”热汤”中的形成过程. 因为在柳絮飞行的过程中, 除了和柳絮进行碰撞, 还能够和其他的东西融合碰撞(比如上面照片中, 角落里的柳絮团上就带了一只死蚊子). 就像是原始的细胞, 在一堆有机分子的相互碰撞下, 形成了一个团状的结构. 但是在像柳絮在地面上滚动沾上灰尘类似的过程中, 产生了细胞膜的结构. 并且像柳絮团一样, 里面也有比较复杂的结构, 并不是一团均匀的物质.
或者是研究絮状沉淀物的生成速度之类的东西?
后记
(本人能力有限, 解释不一定正确. 如有问题, 请指出. )
我的模型的基本思路就是热学课上学到的平均自由程加上一个成团概率.
但是其实这个问题不可能仅仅只用这么简单的模型就能够解释的吧. 后续还能够考虑的因素可以有:
- 考虑空气流动造成的影响, 如: 气流涡旋对成团概率\(P\)的影响, 因为空气阻力导致的大团柳絮运动速度的变化等等. (感谢一个19级的学长的建议)
- 考虑不同柳絮结构对碰撞过程中概率\(P\)的影响, 比如在前面的观察中发现, 有成球状的和散开形状的不同的柳絮团结构. 成球状的不容易和外界继续联系(我的猜测是因为在地面上滚动, 表面带有了一层灰尘, 形成了类似于”保护膜”一样的结构. ), 虽然在实际的观测中, 因为测量仪器(我, 农民的手指头)的灵敏度的限制, 导致了并没有观测到在力学性质上的不同.
- 该模型在其他领域的作用. 比如一位17级的学长提到天文学中的暗物质晕的并合(高斯场中的随机行走). 虽然不知道具体是在说什么, 我还很菜. orz.
嗯, 那么小伙, 你的热学复习呢…
(危)