Optics
光学
怎么说吧, 说难不难, 说简单不简单.
数学
-
Eular Equation:
\[e^{i \theta} = \cos \theta + i\sin \theta\] -
解析拓展
可以用来对表达式进行展开, 同样的可以用来定义算符函数: $f(D) = \sum \cdots$, 比如: $e^{\mathrm{d}/ \mathrm{d}x} = 1 + \mathrm{d}/ \mathrm{d}x + \cdots$. -
傅里叶展开
\[f(x) = \frac{a_0}{2} + \sum_{j=1}^{\infty}(a_j\cos\frac{2\pi jt}{T}+b_j\sin\frac{2\pi jt}{T})\]傅里叶变换
\[f(t) = \int_{0}^{\infty}F(\omega)e^{-i\omega t-\varepsilon\vert \omega \vert}\mathrm{d}\omega, F(\omega)\frac{1}{2\pi}\int_{-\infty}^{\infty}f(t)e^{i\omega t-\varepsilon\vert t\vert}\mathrm{d}t, \varepsilon \rightarrow 0\]
光的传播
首先, 光是电磁波: (可见光范围 $380 \sim 780 nm$)
一般用电场分量来代表电磁波, 如简单的单色平面波:
\[\boldsymbol{E} = \boldsymbol{E}_0 \cos(\omega t - \boldsymbol{k} \cdot \boldsymbol{r} + \psi_0)\]波矢方向 $\boldsymbol{k} = -\nabla\psi$, 磁场与电场正交: $\boldsymbol{B} = \frac{\boldsymbol{k} \times \boldsymbol{E}}{\sqrt{\varepsilon \mu}}$, 于是能流密度 $\langle \boldsymbol{S} \rangle_t = |\boldsymbol{E}| \frac{n}{2\mu_0 c} \frac{\boldsymbol{k} }{k} $.
这样的理想平面波应该有:
- 增幅 $\boldsymbol{E}_0$ 为常量
- 相位梯度 $\boldsymbol{k} = - \nabla \psi$ 为常量
对于不同尺度下的问题, 需要考虑和用来分析的手段也不一样:
- $\rho > 10^3 \lambda$: 这个时候几乎不衍射, 可以用几何光学来近似
- $\rho \sim \lambda, 10^3 \lambda$: 这个量级之间, 考虑衍射
- $\rho < \lambda$: 这个量级衍射图样趋于消失, 以光的散射为主.
几何光学
费马原理
\[\delta L = \delta\int_P^Q n \mathrm{d}l = 0\]证明就利用一个简单的公式:
\[\varphi(Q) - \varphi(P) = -\int_P^Q \nabla \varphi \cdot \mathrm{d} l\] \[\boldsymbol{a} \cdot \boldsymbol{b} \leq \|\boldsymbol{a}\|\|\boldsymbol{b}\| \Rightarrow - \nabla \varphi \cdot \mathrm{d}\boldsymbol{l} \leq \|\nabla\varphi\| = n k \mathrm{d}l\]于是完工.
Note: 用流体的角度来看, 光在一个流管内传播, 光线和能流密度相切, 流管里面的能量不会流出. 光强与截面乘积为不变量.
这样就可以得到一些几何光学的结论了.
几何光学光束
如果增幅变化缓慢, 相位梯度变化缓慢, 那么可以认为一束光就是平面波.
考虑在 \(\boldsymbol{e}_\alpha, \boldsymbol{e}_\beta\) 的基上对电场分量进行分解: \(E_\alpha + E_\beta\).
- 增幅变化缓慢: \(\mathrm{max} \{\vert\frac{\partial \varphi}{\partial \alpha}\vert\} \gg \mathrm{max} \{\frac{1}{A_\alpha} \frac{\partial A_\alpha}{\partial \beta}\}\)
- 相位变化缓慢: \(\mathrm{max} \{\frac{\partial \varphi}{\partial \alpha}\} \gg \mathrm{max} \{(\frac{\partial \varphi}{\partial \beta})\}\)
光线方程
\[\frac{\mathrm{d}^2 \boldsymbol{r}}{\mathrm{d}\tau^2} = n\nabla n = - \nabla V_{=C - \frac{1}{2} n^2}\] \[\frac{\mathrm{d} }{\mathrm{d} s} (n \frac{\mathrm{d} \boldsymbol{r} }{\mathrm{d} s} ) = \nabla n\]前一个的可以和粒子的运动方程类比, 计算起来会比较简单, 后一个和前一个等价就是了.
证明方法就是利用 $-\nabla \varphi = nk\frac{\mathrm{d} \boldsymbol{r} }{\mathrm{d} s}$.
然后两边除一个 $k$, 再对 $s$ 进行一次导数即可.
波动光学
标量波
用复数来描述标量波: (这里的记号是 $e^{-i\varphi}$ )
\[\tilde{U}(P) = A(P)e^{-i(\omega t + \varphi_0(P))}\]波前
使用波前来描述波的性质.
- 平面波: $e^{-i \boldsymbol{k}\cdot\boldsymbol{r}}$
- 球面波: $\frac{A_0}{r} e^{-i \boldsymbol{k}\cdot\boldsymbol{r}}$
- 共轭波
球面波的平面波近似条件:
- 傍轴条件: $z^2 \gg \rho^2$
- 远场条件: $e^{i \frac{\pi \rho^2}{z \lambda}} \approx 1$
Note: 一般这样的 $\gg$ 可以用 $50 \sim 100$ 倍来简单近似, 不过貌似作业里面用 $50$ 的比较多.
记忆: 若将球面波视为沿 $z$ 轴传播的一束平面波 $e^{i k z}$ 的话, 对球面波的 $r$ 有展开 $r = z + \rho^2/z - \cdots$, 傍轴条件对应 $ \frac{A_0}{r} \approx \frac{A_0}{z}$, 远场条件对应 $e^{ikr}=e^{ikz}$.
菲涅耳-基尔霍夫积分
\[U(P) = \frac{-i}{\lambda} \oiint_{\Sigma}(\frac{\cos\theta + \cos\theta_0}{2}) U(Q) \frac{e^{i k r}}{r} \mathrm{d} S\]互补原理
假如有两个互补屏, 那么经过它们的衍射结果相同: $I_{+} = I_{-}$.
衍射系统
选择一个波面, 其包含的包括光源所在的空间为照明空间, 其外为衍射空间, 在衍射空间中的点 $P$ 感受到的光强就是该波面上的子波源在这一点的光强的 贡献的统计平均.
-
夫琅和费衍射: 相对衍射屏接受场和光源都满足远场条件, 通过凸透镜将光源聚焦在成像面上 (或者在远处接收)
单缝夫琅和费衍射:
\[A \propto \int_{-1}^{1} \frac{\mathrm{d}x}{2} e^{-ikx\sin\theta} = \frac{\sin(k\sin\theta)}{\sin\theta} \Rightarrow I = I_0 (\frac{\sin(k\sin\theta)}{\sin\theta})^2\]圆孔的夫琅和费衍射:
\[U(P) = \frac{- i A}{F \lambda} e^{ikL_0} 2\pi\int_0^a \mathrm{d}\rho\rho e^{-ik\rho\cos\phi\sin\theta} = \frac{\pi a^2}{F\lambda}\frac{2J_1(\gamma)}{\gamma}, \gamma = ka\sin\theta, J_1: Bessel\]反正也没法继续算了, 知道一下结论: $\theta = 0 \Rightarrow I = (\frac{\pi a^2}{F\lambda})^2 I_0$, 半角 $0.61 \frac{\lambda}{a}$ 其中 $F$ 为透镜焦距
-
菲涅耳衍射: 都不满足远场条件
圆孔菲涅耳衍射:
\[U(P) = \frac{-i}{2\lambda} \iint \frac{e^{ikr_1}}{r_1}(\cos\theta_1 + \cos\theta_2)_{\approx F(0) = \frac{1}{r}} \frac{e^{ikl}}{r+l} \mathrm{d}l\]实际上可以直接用半波带方法会比较快:
\[n = \frac{\rho^2}{2} (\frac{1}{a} + \frac{1}{b})\]半无穷大屏菲涅耳衍射:
同上, 也能够用积分来做. 就是比较麻烦而已
波的矢量性 - 菲涅尔
将光分成 $s$ 波和 $p$ 波 (垂直 straight, 平行 parallel 分量), 在分界面上有电磁场连续方程: $\varepsilon E, \mu H$, 并且利用 $\sqrt{\varepsilon} E = \sqrt{\mu} H, n = \sqrt{(\varepsilon/\mu)/(\varepsilon_0/\mu_0)} \Rightarrow H = n E$ 来将所有的 $H$ 都用 $E$ 来标识. 于是有方程:
\[\begin{array}{lll} r_s & = & \frac{n_1 \cos i_1 - n_2 \cos i_2}{n_1 \cos i_1 + n_2 \cos i_2}\\ t_s & = & \frac{2 n_1 \cos i_1}{n_1 \cos i_1 + n_2 \cos i_2}\\ r_p & = & \frac{n_2 \cos i_1 - n_1 \cos i_2}{n_1 \cos i_2 + n_2 \cos i_1}\\ r_s & = & \frac{2 n_1 \cos i_1}{n_1 \cos i_2 + n_2 \cos i_1} \end{array}\]Note: 记不住的话…
\[\begin{array}{lll}E_{1,s} + E_{1,s}' & = & E_{2,s}\\E_{1,p} - E_{1,p}' & = & E_{1,p}\\ n_1 (E_{1,s} - E_{1,s}') & = & n_2 E_{2,s}\\n_1(E_{1,p}+E_{1,p}') & = & n_2 E_{2,p}\end{array}\]
上面的都是对光的增幅 (电场振幅) 的东西, 对于光强 (功率) 来说, 则是:
\[R_p = \vert r_p \vert^2, R_s = \vert r_s \vert, T_p = \frac{n_2}{n_1} \vert t_p \vert^2, T_s = \frac{n_2}{n_1} \vert t_s\vert^2\] \[R + T = 1, T \cos i_2 + R \cos i_1 = \cos i_1, n_2 \vert t \vert^2 \cos i_2 + n_1 \vert r \vert^2 \cos i_1 = n_1 \cos i_1\]对于临界情况:
- 布儒斯特角: $r_p = 0 \Rightarrow i_B = \tan^{-1}\frac{n_2}{n_1}$
- 临界角: $T = 0 \Rightarrow i_c = \sin^{-1}\frac{n_2}{n_1}$
- 正入射: $r_p = -r_s = \frac{n_2 - n_1}{n_2 + n_1}, t_p = t_s = \frac{2n_1}{n_2 + n_1}, R = (\frac{n_2 - n_1}{n_2 + n_1})^2, T = \frac{4n_1n_2}{(n_2 + n_1)^2}$
倒逆关系: 假如从 1 到 2 介质是 $t, r$, 那么从 2 到 1 是 $t’, r’$:
\(r^2 + tt' = 1\) \(r' = -r\)
Note: 证明和记忆
$r’ = -r$: 相对轴做对称, 前者是能量
Note: 推广的斯托克斯倒逆关系
\[\vert r^2 \vert + t' t= 1, r^* t + r' t^* = 0\]这样的证明方法就是考虑共轭波的入射和反过来的轨迹, 对这样的结果, 会有 $r r^* + t’ t^* = 1, r^* t + r’ t^* = 0$
全反射的相位变化:
| 入射角 | 切线分量 | 法相分量 |
| $<i_b$ | $0$ | $\pi$ |
| $>i_b,<i_c$ | $-\pi$ | $0$ |
| $>i_c$ | $(-\pi,0)$ | $(0,\pi)$ |
| $\pi/2$ | $0$ | $\pi$ |
Note: 其实直接计算可以发现 $r_p = \vert r_p \vert e^{-i \delta \phi}$ 就能够知道相位变化了
利用这个性质就能够发现, 经过反射可以导致 $p$, $s$ 波的 方向变化, 从而有对偏振态的影响. 比如椭圆光经过反射, 让一个分量的光产生了相位差, 和另一个分量的光之间的相位相同或相差了 $\pi$, 那么就会从椭圆光变回线偏振光.
波的矢量性 - 光的在晶体中的传播
电磁波在晶体中传播, $\boldsymbol{S} = \boldsymbol{H} \times \boldsymbol{E}$, 但是非各向同性的介质中 $\boldsymbol{D} = \boldsymbol{\varepsilon}\boldsymbol{E}$ 不一定和 $\boldsymbol{E}$ 平行. 可能会有一个 $\alpha$ 夹角. 而 $\boldsymbol{k}$ 和 $\boldsymbol{D}, \boldsymbol{H}$ 垂直, 想要计算波矢, 也就是传播方向, 就需要知道 $\boldsymbol{D}$.
\[\boldsymbol{k} \times \boldsymbol{H} = - \omega \boldsymbol{D}, \boldsymbol{k} \times \boldsymbol{E} = \omega \mu \boldsymbol{H} \Rightarrow k^2 \frac{\varepsilon_0\boldsymbol{E}\cdot\boldsymbol{D}}{D^2} = k_0^2 = (\frac{\omega}{c})^2\]在晶体中的传播分成 $o$ 光和 $e$ 光,
- 定义光线传播方向和光轴 (下记为 $z$ 轴) 的平面为主平面
- 定义 $o$ 光为振动方向和主平面垂直的光, 和光轴垂直, 所以传播方向没什么变化. 就是普通的折射定律就能够计算了.
-
定义 $e$ 光为振动方向和主平面平行的光, 在三维上面, 就是和 $z$ 轴平行的 $D_{ez}$ 分量和 $z$ 轴垂直, 但是在主平面上的 $D_{e\bot}$ 分量, 于是有:
\[D_{ez} = \varepsilon_0 n_e^2 E_ez, D_{e\bot} = \varepsilon_0n_o^2E_{e\bot} \Rightarrow \varepsilon_0 E_e \cdot D_e = \frac{D_{ez}^2}{n_e^2} + \frac{D_{e\bot}^2}{n_o^2} \Rightarrow (\frac{k_z^2}{n_o^2} + \frac{k_x^2+k_y^2}{n_e^2}) = k_0^2\]
Note: 双轴晶体就略去了.
同理, 可以计算光线相速度 $\boldsymbol{ v} = \frac{\boldsymbol{k}}{k}\frac{\omega}{k}$. 以及光线速度: $\boldsymbol{ v}_r = \frac{\boldsymbol{S} }{w}$
( 啊, 这里好麻烦哦, 一个麻烦的地方就是要记住自己在考虑什么问题, 经常会把 $o$ 光还是 $e$ 光搞混, 这个时候, 一个帮助自己搞清楚自己到底在干什么的方法就是: 去想 $o$ 光就是 ordianary 光, 传播方向和各种结论都和普通的, 那种初级的结论一样, 那么为什么要为它伤脑筋呢? 所以关注 $e$ 光看起来会比较合理. )
有了上面那段思考之后, 发现问题变得简单了: 什么垃圾晶体光学, 实际上对于单轴晶体来说, 问题很简单: 沿着 $z$ 轴和垂直 $z$ 轴的光的速度不一样, 分别记为 $n_e$ 和 $n_o$ 来表示. 对于直接规定垂直 $z$ 轴振动的 $o$ 光, 很显然, 是各项同性的, 而对于规定的 $e$ 光, 部分垂直, 部分平行, 所以光的传播和速度都会随着方向而改变:
假设 $e$ 光的波矢和 $z$ 轴的夹角为 $\theta$, 那么沿着 $z$ 轴的分量和垂直 $z$ 轴的分量就要满足条件: $ (\frac{k_x}{n_e})^2 + (\frac{k_z}{n_o})^2 = k_0^2, k_x = k\sin\theta, k_z = k\cos\theta \Rightarrow v_p^2 = v_o^2\cos^2\theta + v_e^2 \sin^2\theta$
但是波矢的方向是相速度的方向不是光线速度的方向, 光线速度的方向和等相位面垂直 ( 这个是几何的观点 ), 或者干脆直接从分量之间的关系来可能会更好记:
\[\frac{D_z}{D_x} = \frac{n_e^2}{n_o^2} \frac{E_z}{E_x} \Rightarrow \tan\theta = \frac{n_e^2}{n_o^2}\tan\xi\]( 可惜上面分析了这么多, 只不过是光线在晶体里面的传播规律而已, 我想要知道的是光线从外面入射会发生什么的结论啊… )
$o$ 光不看了, 只关心 $e$ 光:
在分界面上, 考虑波矢的切向分量连续: $\boldsymbol{e}_n \times (\boldsymbol{k} - \boldsymbol{k}_1) = 0$. 然后经过漫长的计算, 应该可以得到结果. ( 太长了, 算了. )
双折射作图法: ( 不关心 $o$ 光, 这里是 $e$ 光的回合)
(平面光波入射, 主截面和入射面一致)
- 画出界面, 光轴, 折射率圆 ( 对应空气, 半径为 $n_1$)和折射率椭圆 ( 对应 $e$ 光, 在光轴上和 $o$ 光的圆重合, 垂直光轴的那个轴的长度为 $n_e$)
- 画出过圆心的入射光线, 过入射光线和入射折射率圆交点作出界面法线, 连接圆心和法线于折射率椭圆的交点, 得到 $e$ 光波矢方向, 过波矢和折射率椭圆的交点作折射率
光的统计
两个光相加 ($I = \langle \tilde{U}(P) \rangle$):
\[I = I_1 + I_2 + 2\langle \tilde{U}_1^*(P)\tilde{U}_2(P)\rangle\]可以发现, 在上面的 $\langle \tilde{U}_1^*(P)\tilde{U}_2(P)\rangle$ 部分, 是影响最终的光强的主要变动项. 引入相关系数 \(R = \frac{\langle \tilde{U}_1^*(P)\tilde{U}_2(P)\rangle}{\sqrt{\langle \vert\tilde{U}_1(P)\vert^2\rangle \langle \vert\tilde{U}_2(P)\vert^2\rangle}} = \mathrm{Cov}(I_1 I_2) \Rightarrow I(P) = I_1 + I_2 + 2\vert R\vert\sqrt{I_1(P)I_2(P)}\)
影响最终光强结果的主要还是后面的平均项, 也就是统计的部分. 而根据对什么东西统计, 就会得到空间相干性和时间相干性的不同的结果.
对于可视度: $\gamma = \frac{I_M - I_m}{I_M + I_m}$, 当 $\gamma = 0$ 的时候, 认为是非相干, $=1$ 时为完全相干.
空间相干性
在考虑空间相干性的时候, 使用波列模型来考虑问题: 认为一束光的相位 $\phi = \boldsymbol{k}\cdot \boldsymbol{x}+ \omega t + \delta$, 其中 $\delta$ 为单一频率的光随机涨落的相位差.
对于一个良好的干涉光, 应该满足: $\vert T \frac{\partial}{\partial t}\delta(P)\vert\ll 1$, 即 $(\omega_1-\omega_2)T+T \frac{\partial }{\partial t} \delta(P,t)\vert\ll 1$. 即在一个周期里面相位变化应该不太大.
于是得到干涉条件:
- $\omega_1 \approx \omega_2$
- 光矢量不正交
- 相位差无明显涨落 $\frac{\partial }{\partial t} \delta(P)\ll 1$
于是可以把光强写为: $I = I_0(1+\gamma\cos \delta(P))$
杨氏双缝干涉以及其他各种干涉
其实关键就是计算干涉的时候的相位差.
空间相干性的决定因素
对于上面的 $R$ 部分, 可以发现 $\gamma = \vert R \vert\gamma_m$, 于是可以说, 要研究空间相干性的问题的话, 就只需要研究这个 $R$ 的影响因素即可.
对于光源宽度对空间相干性的影响:
\[d_0=1.22\frac{l\lambda }{b}\]即对于一个圆型的光源 $b$, 其对应的相干区域应该不会超过那么大 $d_0$. 其中 $l$ 为距离. 或者干脆写成角度的形式:
\[\Delta \theta_0 = \frac{\lambda }{b}\]时间相干性
考虑迈克尔逊干涉仪中的两个光的叠加:
\[U_1 = \sqrt{\frac{T}{2\pi}}\int_0^{\infty}a(\omega)e^{i(kL_1-\omega t)}\mathrm{d}\omega, U_2 = \sqrt{\frac{T}{2\pi}}\int_0^{\infty}a(\omega)e^{i(kL_2-\omega t)}\mathrm{d}\omega\]应该有相同的频谱, 因为是同一个光源分出来的两个光. 但是考虑 $\tau = \frac{L_1-L_2}{c}$ 也就是因为光程差引入的一个时间差. 于是前面的 \(\langle \tilde{U}_1^*(t)\tilde{U}_2(t)\rangle \Rightarrow \langle \tilde{U}_1^*(t)\tilde{U}_1(t+\tau)\rangle = \int_0^\infty\mathrm{d}\omega\vert a(\omega)\vert^2 e^{-i\omega\tau}=\int_0^\infty\mathrm{d}\omega I(\omega)e^{-i\omega \pi} = G(\tau)\) 称为光源的时间自相关函数, 即光场的归一化功率谱.
可以写成:
\[I(\Delta L) = I(1+\gamma_M\int_0^\infty\mathrm{d}\omega i(\omega)\cos(\frac{\omega\Delta L}{c})), \gamma_M = \frac{2\sqrt{I_1I_2}}{I_1+I_2}\]其中 $\gamma_M$ 为光强不相等时, 可能存在的最大条纹可视度. 对于不同的光源的光谱:
- 高斯型: $I(\omega)=\frac{I}{\sqrt{2\pi}\Gamma}e^{-\frac{(\omega - \omega_0)^2}{2\Gamma^2}} \Leftrightarrow G(\tau) = e^{-i\omega_0\tau}e^{-\frac{1}{2} \Gamma^2\tau^2}$
- 洛仑兹型: $I(\omega) = \frac{I}{\pi}\frac{\Gamma}{(\omega - \omega_0)^2+\Gamma^2} \Leftrightarrow G(\tau) = e^{-i\omega_0\tau}e^{-\Gamma\vert\tau\vert}$
- 理想单色光: $I = \delta(\omega-\omega_0) \Leftrightarrow G(\tau) = e^{-i\omega_0\tau}$
并且其对应的相干时间 $\tau_c = \int_{-\infty}^{\infty}\vert G(\tau)\vert^2\mathrm{d}\tau \Rightarrow \vert G(\tau)\vert = e^{-(\pi/2)(\tau/\tau_c)^2}$:
- 高斯: $\tau_c = \frac{\sqrt{\pi}}{\Gamma } \approx \frac{4.174}{\Delta \omega} \Rightarrow \vert G(\tau)\vert = 0.2079$
- 洛仑兹: $\tau_c = \frac{1}{\Gamma} = \frac{2}{\Delta\omega} \Rightarrow \vert G(\tau)\vert = 0.3679$
( 相干长度: $L_c \approx c\tau_c$ )
迈克尔逊干涉仪
基本的原理就是改变两个臂之间的距离来产生光程差.
- 分波幅装置
- 两个光束传播方向垂直
- 光程差可以在大范围内调节
- 两个光路之间有较大的操作空间
波包
偏振
在偏振里面: $R = e^{i\delta}$
-
马吕斯
\[I(\alpha) = I_0 \cos^2\alpha\] - 检验和产生
- 使光通过 $\lambda/4$ 波晶片
- 测量表观偏振度, 为原来光波的偏振度
- 等效表达
- 相干性
例题
- 光的本性
光是波: $k = \frac{2\pi}{\lambda}, \nu = \frac{c}{\lambda} = \frac{1}{T},\lambda = \frac{\lambda_0}{n} $
已知光强或者辐射强度, 计算电场振幅或者方均根.
- 一个激光功率 $100mW$, 截面光强分布为 $I(r) = I_0 E^{-r^2/r_0^2}$ 光束中心处电场振幅 $P = 2\pi \int_0^\infty I(r)r \mathrm{d}r = \pi r_0^2 I_0 \Rightarrow \frac{P}{\pi r_0^2} = I_0 = \frac{c \varepsilon_0 E_0^2}{2} \Rightarrow E_0 = \sqrt{\frac{2I_0}{c\varepsilon_0}}$.
- 地球大气外层太阳辐射强度为 $P/\Delta S \Rightarrow E_{r.m.s} = \sqrt{I / (c \varepsilon_0)}$.
利用的结论是 $I = c \hat{\omega}$, 但是在平均的时候, 需要注意对不同的光会有不同的结果:
- 单色光: $\hat{\omega} = \langle \varepsilon_0 E_0^2 \cos^2 \omega t \rangle_t$
- 太阳光(自然光, 非单色光): $\hat{\omega} = \hat{E^2}$, 只能得到方均根.
- 几何光学
计算三棱镜的最小偏向角的位置和折射率
(Note: 轴对称的时候最小, $\delta_m = 2 \arcsin(n\sin \frac{A}{2}) - A$)折射率随着界面连续变化:
- $n_k \sin i_k = n_j \sin i_j$, 入射角连续变化
- 或者利用运动方程 $ \frac{\mathrm{d}^2 \boldsymbol{r}}{\mathrm{d}\tau^2}$ 来计算
- 对于圆柱型的, 上面的运动方程还能够类比角动量守恒来求解.
利用 $\frac{\mathrm{d}^2 \boldsymbol{r}}{\mathrm{d} \tau^2} = \frac{1}{2} n^2$ 来计算运动轨迹
\[n(z) = n_0 (1+az), a>0 \Rightarrow z \approx \frac{1}{2} n_0^2 a \tau^2 + v_z \tau \Rightarrow 抛物线\] - 利用半波带法计算振幅
遮罩屏: (平行光照明, 有这样的遮罩, 求中心光强)
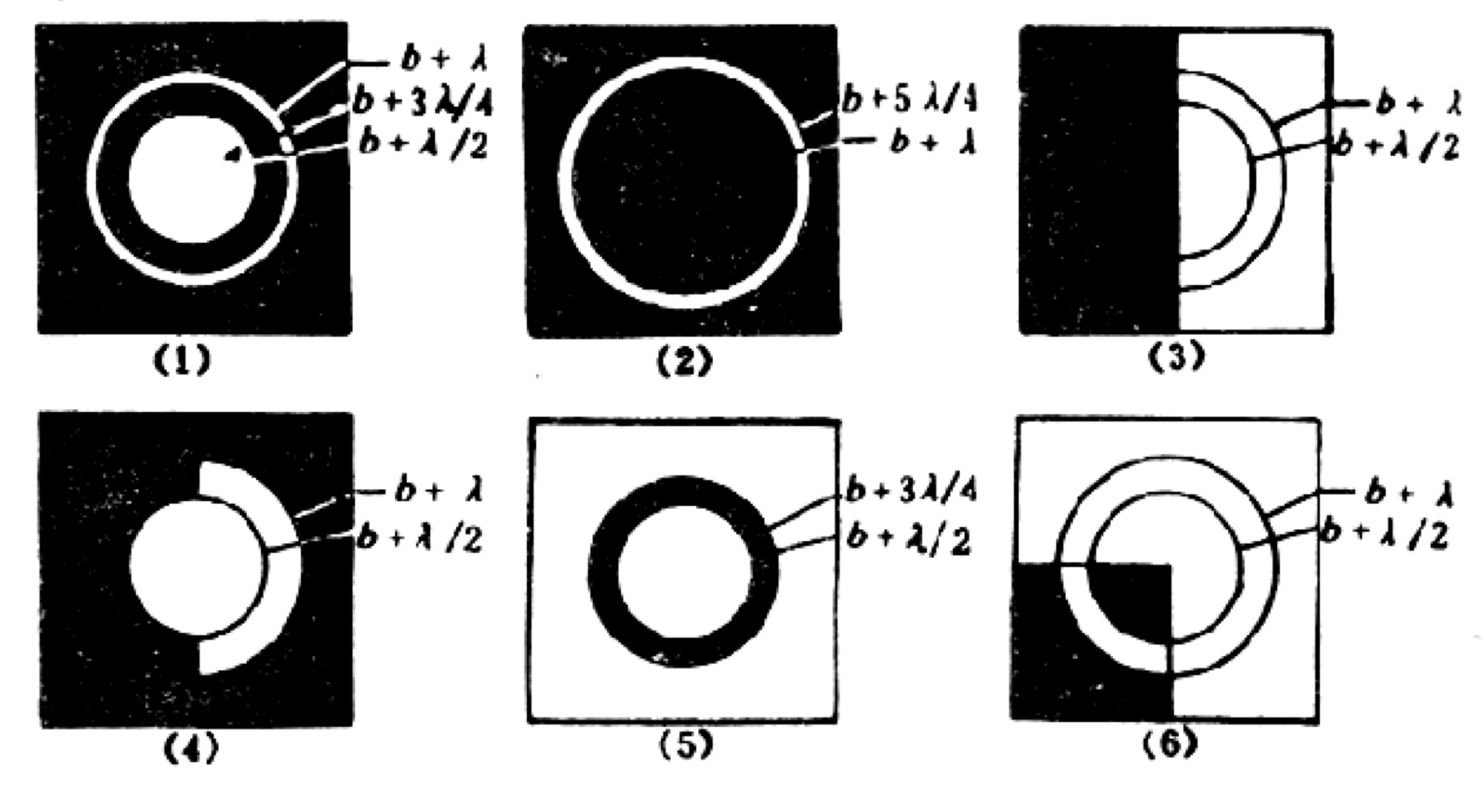 这个题目的关键应该就是如何数半波带了,
数了半波带之后用矢量合成的方法来计算
这个题目的关键应该就是如何数半波带了,
数了半波带之后用矢量合成的方法来计算- (1): 包含了 $0, \lambda /4, \lambda /2, \lambda$ 波带, $A = \sqrt{2} A_0 \Rightarrow I = 2 I_0$
- (3): 只有一部分的话, 可以看作有全部, 然后减去. $A \rightarrow A_0/2$
- (5): 利用互补原理, 互补屏的光强相等
- (6): 综合了属于是, 这样的话就是 $A \rightarrow A_0/4$
- 各种衍射问题的应用
圆孔衍射中暗环的数量:
就是将圆孔半径 $\rightarrow 0$, 中心出现暗点的次数.圆孔光轴上的光强: $A = 2 A_0 \sin \frac{\delta}{2}, \delta = \frac{2\pi}{\lambda }\frac{\rho^2}{2b}$
针孔照相机的最佳成像:
- 光轴光强最大 $ \rightarrow $ 奇数个半波带
- 一个物点一个光斑 $ \rightarrow $ 只有一个半波带
$ \Rightarrow d = 2 \rho = 2 \sqrt{\nu \lambda}$
(Note: 这里的 $\rho$ 需要满足远场条件, 是用远场条件来算的. 类似的, 通过光导轨的长度来计算圆孔最佳直径也是这样的: $\frac{\rho^2}{z \lambda} \leq 0.01 \Rightarrow d \leq 0.1 \rho\sqrt{z \lambda}$) 针孔照相机的像点位置: 只包含一个半波带: $\rho_1 = \frac{d}{2}, \rho_1 = \frac{\lambda a b}{a + b}$
用积分暴力算光强分布
- 菲涅耳公式
光强计算
- 光强为 $I_0$, $i_B$ 从 $n_1 \rightarrow n_2$, 计算光强
因为是 $i_B \Rightarrow r_p = 0 \Rightarrow r_s = \frac{n_1^2 - n_2^2}{n_1^2 + n_2^2} \mathrm{or} I_0 \cos i_1 = I_1 \cos i_1 + I_2 \cos i_2$.
后一个公式利用了能流密度(能量守恒) - 圆偏振光的上题版本
$I = I_p + I_s$
相位差计算: (看 $r_s, r_p$ 的正负知相差是 $0 \mathrm{or} \pi$)
- 线偏振光入射到直角等腰棱镜上, 发生两次反射, $s,p$ 振幅变化和相位变化.
振幅变换就是 $\frac{A_s}{A_p} = \vert \frac{r_s}{r_p}\vert^2$, 相位变化则是通过计算 $r_p = \vert r_p \vert e^{-i\phi}$ 来得到 $\phi$ 的变化. - 圆偏振光从 $n_1 > n_2$ 入射, 计算反射光的偏振态
- 光强为 $I_0$, $i_B$ 从 $n_1 \rightarrow n_2$, 计算光强
- 双折射
计算 $e$ 光的各种信息
波长, 相速度, 光线速度, 和光轴夹角等等- 已知波矢方向和光轴方向的夹角 $\theta$, $ \Rightarrow \frac{1}{n(\theta)}=\sqrt{(\frac{\cos\theta }{n_0})^2 + (\frac{\sin\theta }{n_e} )^2}$, 然后是光线速度方向 $\tan\xi = \frac{n_o^2}{n_e}^2\tan\theta$, 以及是光线速度: $\frac{ v_ov_e}{\sqrt{ v_e^2\cos^2\xi + v_o^2\sin^2\xi}} = \frac{c}{\sqrt{n_0^2\cos^2\xi+n_e^2\sin^2\xi }} = \frac{c}{n_on_e} \sqrt{\frac{n_e^4+n_o^4\tan^2\theta }{n_e^2+n_o^2\tan^2\theta }}$
- 已知光线方向和光轴夹角 $\xi$, $ \Rightarrow \tan\theta =\frac{n_e^2}{n_o^2} \tan\xi$
- 光线速度和波矢的最大夹角
- 晶体光学原件
- 晶体棱镜: 用于产生和检验偏振光
-
分离器: 利用 $o$ 光 ( 或 $e$ 光)全反射, $e$ 光 ( 或 $o$ 光)部分透射的方法分离 $e,o$ 光得到偏振光.
计算分束角, 计算棱镜夹角
- 补偿器: 在光矢量正交分量之间引入线性相位差
- 波晶片: 厚度均匀, 光轴平行表面的单轴晶体薄片, 所以 $o$, $e$ 光在其中传播方向不改变, 但是因为光的相速度不一样, 所以会有相位差. $ \delta = \frac{2\pi}{\lambda}(n_e -n_o)d$
计算 $1/4$ 波晶片的厚度 $(n_e-n_o)d=(2k+1)\frac{\lambda }{4}$
-
- 晶体棱镜: 用于产生和检验偏振光
- 旋光: $\phi = \alpha d, \alpha = \frac{\pi}{\lambda} (n_L - n_R)$, 或者在溶液里面: $\phi = [\alpha]N_{浓度}d$
- 磁致旋光: $\phi = VBl$, 不可逆.
- 干涉
使用杨氏双缝来进行实验, 知道光源波长 $\lambda$, 双孔间距为$d$, 双孔到接受屏的距离$D$, 双孔到单孔的距离 $l$, 求弹孔移动 $s$ 之后, 中心干涉条纹移动的数目 $N$
这个其实就是考虑单孔移动 $s$ 后给系统增加的初始相位差 $\delta_0 = \frac{D}{l} s$, 于是就能够用 $N = \frac{\delta x}{\Delta x}$ 来计算移动的条纹数量.单缝倾斜 $\alpha$ 角度 ( 以光线传播方向为轴) 后, 干涉条纹的可视度的改变情况
一个简单的作法就是把单缝的倾斜看作是光源的变宽, 然后利用临界光源宽度: \(d_0=1.22\frac{l\lambda }{b}\) 来计算即可. 或者干脆这样: 认为最上面的偏移量和最下面的偏移量对相位差的影响刚好是一个 $\lambda/2$杨氏双缝干涉条纹的间隔的最小值, 已知单孔直径 $\phi$, 双孔到接受屏的距离为 $D$, 双孔到单孔的距离为$R$, 波长 $\lambda$
$d \leq 1.22 \frac{R\lambda}{\phi } \Rightarrow \Delta x = \frac{D}{d} \lambda$ - 自相关函数
已知自相关函数, 求干涉迈克尔逊仪的性质:
- 光强随臂长改变周期: $\Delta L = \frac{\lambda }{2}$, 其实就是臂移动速度和 $\lambda/2$ 的关系
- 可视度在 $L$ 下: $\gamma = \vert G(\tau = \frac{L}{c})\vert$
- 量程: 若可视度要大于 $0.5$, 求量程: $\gamma = \vert G(\tau = \frac{L}{c})\vert > 0.5$
不同波长的光的影响: 有 $\lambda_1, \lambda_2$ 的光叠加在一起, 在迈克尔逊干涉仪里面, 求第一次干涉条纹消失的臂长差 $L$:
- 时间相干性的观点 $I(\tau) = I_0 (1 + \frac{1}{2}(\cos\omega_1\tau + \cos\omega_2\tau))$
- 普通的观点: 认为是两个波长的干涉条纹相互抵消
估计激光光谱宽度: $\Delta \nu \tau \sim 1 \Rightarrow L = c\tau \Rightarrow \Delta \nu \sim\frac{1}{\tau} = \frac{c}{L}$
- 偏振
自然光经过两个正交的偏振片, 在其中加入一个检偏器, 求:
- 透射光最大值: 自然光, 过了第一个偏振片之后剩下 $ \frac{1}{2} I_0$, 过了第二个之后再过第三个, 注意每个的叠加就好了: $I=(1/2)I_0\cos^2\alpha\sin^2\alpha$
- 旋转一周消光量
透过检偏器的一束光光强随着透振方向改变, 测得最大光强和最小光强分别是 $5I_0, 3I_0$: $I(\alpha) = I_m + (I_M - I_m)\sin^2\alpha = I_M + (I_M - I_m)\cos^2\alpha$
计算光的偏振度: 把任意偏振光看作是自然光和椭圆偏振光的非相干叠加, 认为自然光光强 $I_0$, 椭圆偏振光光强 $I_p$, 椭圆长短轴比为 $\tan\theta$, 于是 $p = \frac{(\frac{1}{2} I_0 + \cos^2\theta I_p) - (\frac{1}{2} + \sin^2\theta I_p)}{(\frac{1}{2} I_0 + \cos^2\theta I_p) + (\frac{1}{2} + \sin^2\theta I_p)} = P\cos 2\theta$
(Note: 偏振度: $P = \frac{I_L - I_R}{I_L+I_R}$, 表观偏振度 $p = \frac{I_M-I_m}{I_M+I_m} $)
后记
淦, 为什么不带计算器?