[Lecture] The Hydrodynamic Limit of Boltzmann

[Lecture] The Hydrodynamic Limit of Boltzmann - Feimin Huang

感觉的这个讲座挺有意思的, 所以做一个小小的笔记.

免责申明: 我也不是数学系的, 我也不是特别懂, 里面所有的注记都是我瞎想的. 所以不一定正确… 并且这个笔记并不是对讲座的完整记录, 只是我从我的破烂手写笔迹纸上散乱的字迹中辨认重组得到的一些胡言乱语罢了.

Eular & Navier-Stokes Equation – Continuous Concept

The Eular Equation considers the ideal fluid, which is based on conservation of mass, energy, momentum.

\[\begin{array}{llll} \frac{\partial \rho}{\partial t} + \boldsymbol{v} \nabla \rho & = & 0 & \mathrm{Mass\ Conservation} \\ \frac{\partial \boldsymbol{v}}{\partial t} + (\boldsymbol{v} \cdot \nabla) \boldsymbol{v} & = & \boldsymbol{F} - \frac{1}{\rho} \nabla \rho & \mathrm{Energy\ Conservation}\end{array}\]

具体的推导就暂时不管了. 但是在 Eular 方程中, 总是存在这样的一个假设, 认为总能够找到一个微元, 然后能够通过对其使用物理定律的方式来得到物理方程.

比如对一个封闭曲面进行考虑: $\oint_S \boldsymbol{v} \mathrm{d}\boldsymbol{S} = - \frac{\partial}{\partial t} \int_V \rho \mathrm{d}V$, 然后取微元得到极限即可.

在讲座中, 老师提到的 Eular 方程中这样的操作其实是建立在认为空间是连续的, 或者这样说: 被研究的流体被认为在空间上是连续分布的.

同样的, 作为千禧年问题 (7 Millenium Prize Problems in 2000) 中的一个的 Navier-Stokes Equation, 其也是和 Eular 公式一样, 应该也是建立在研究对象 是在空间中连续分布的基础之上的.

(注: 但是千禧年问题是由 Charles Fefferman 提出的: The existence and smoothness of Navier-Stokes Equation. 即 NS 方程的存在性和连续性. 据老师所讲, 目前有两种观点, 一种认为湍流现象 是可以被 NS 方程所解释的, 也就是说, NS 方程是连续的; 而另外一种, 则是认为 NS 方程不连续, 所以湍流是反对. 但是不论怎么说, 目前应该是谁也不知道. )

而根据考虑的情况, 可以将被研究的对象分为可压缩的(compressible), 和不可被压缩的(imcompressible). 于是就有了四种方程: C.E, IC.E, C.NS, IC.NS. 也就是 (可压缩 / 不可压缩) 的 (Eular / Navier-Stokes) 方程.

Shock Waves – 连续函数的概念的消失

Shock Waves, 也就是激波, 定义为: change quickly in a very small region. 即在小区域内快速变化的运动形式. 常见的例子就是超过音速的飞机会挤压空气, 然后形成一个阶越变化的感觉. emmm… 感觉还是找图片会比较好理解:

( 图片来源于NASA. )

其中那些明显变暗的部分就是因为被剧烈压缩导致的空气急遽变化的区域. 而正是这样的区域: not continuous at some points in mathematics, 导致了在上面的 Eular 或 Navier-Stokes 方程中出现的偏微分就失去了意义. 或者说, 至少是有待重新商榷.

( 这里应该有一张倒地的自行车的表情包: 可导连续, 连续不可导, 不连续… )

Boltzmann – Stastical Concept

虽然一开始我并没有从讲座的标题 Boltzmann 上想到那个热学里面大名鼎鼎的 Boltzmann, 但是当老师开始讲下面那段话的时候, 我确实是不由自主地在纸上写下了两个大字: “ 统计 ?”.

for $n$ particals in $V$, they have $6$ freedom and …

Boltzmann 的观点应该是一种统计的观点, 当 $\lim n \rightarrow \infty$ 时, 对系统中的粒子取统计平均 ( 害, 热学还没有怎么搞太懂, 现在还开始热统了. )

( 注: 这个工作其实 Maxwell 做得比较早, 但是因为 Maxwell’s Equations 实在是太出名了 – 毕竟是和 Newton 三定律一样的开辟了科技革命的东西, 所以人们往往还会把 Maxwell Distribution 给忘了. 其实不只是 Maxwell, 比如 Zuqia Huang, 在中国搞核工程的老前辈, 著有《输运理论》, 是以前 氢弹研发中的一个组 – 当时有三个组, 但是现在更加闻名的应该是于敏. )

( 又: Boltzmann 的这个理论在一开始是受到非常多人的反对的, 比如马赫就和他反复探讨, 结果最终实在没法反驳, 于是就说: atoms and moleculars do not exist – 毕竟当时没有这个观念. 最后 Boltzmann 因此也 depressed, 最终自杀了. 而更加悲剧的是, 在他死后几年(5 年), 人们就观测到了原子分子存在的证据了… )

\[f_t + \boldsymbol{v} \cdot \nabla f = \frac{1}{\varepsilon} Q(f, f)\]

其中: $f_t$ is the density distribution function of particals (密度分布函数), $\varepsilon$ is Knudsen number(free path) (自由程), $Q$ is Collision Operator.

于是数学家就能够用这样的方式来从 Newton 的范式转移到 Boltzmann 的统计的范式, 并且还能够发现更棒的事情就是, 这样的新的范式能够在一定的极限下得到原本的方程.

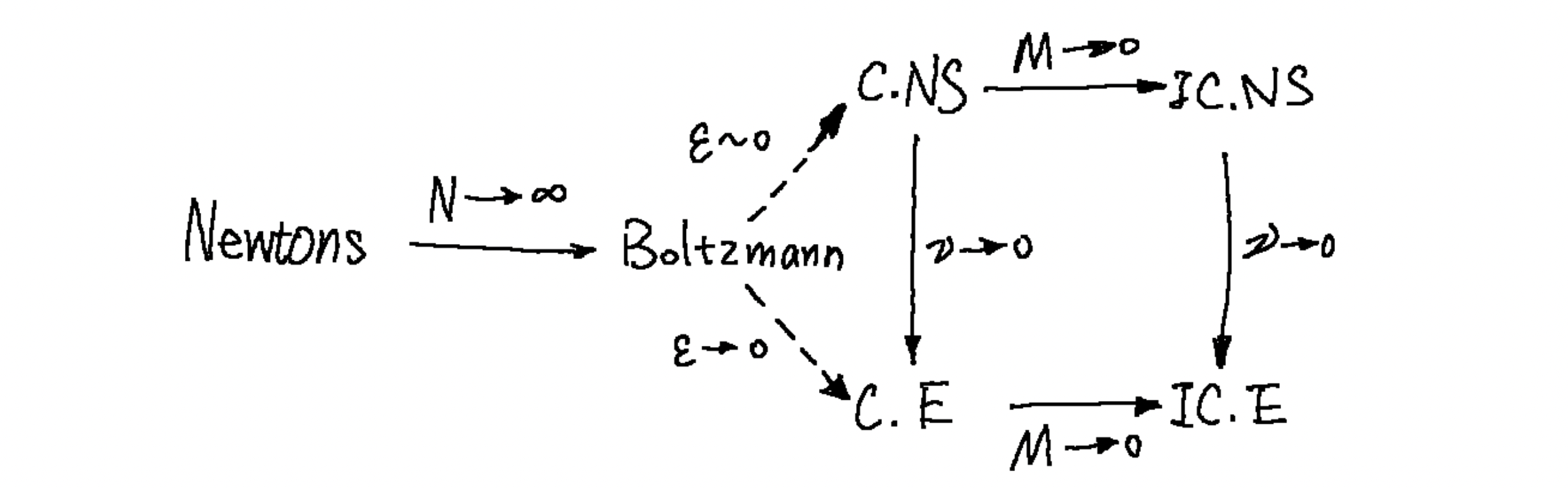
其中, $\varepsilon$ 代表 free path ( 自由程 ), $\nu$ 代表 viscosity ( 黏性 ), $M$ 代表马赫数. 于是数学上就能说, C.NS, IC.NS, C.E, IC.E 这些方程就是 Boltzmann 的一些极限.

于是数学家就很开心了: 这样我们就连物理实验都不用做了. ( 狂言, 一定是狂言… )

( 注: 虽然我觉得, 对 David Hillbert 的那个问题 – Mathematical treatment of the axioms of physics – 应该这么看: 就是对于物理中的那些简单的方程, 将其用数学的框架严格化和标准化; 而物理中用到的那些奇怪的方程, 现有的数学无法解释, 就需要拓展数学的框架来包含. 目前是这么想的, 毕竟还是一个物理系的 ( 菜狗 ). )

不过这个时候, 之前力学课上的一种对 Eular 公式的解释估计就比较贴近了: 宏观无穷小, 微观无穷大. 就宏观无穷小的部分让这个方程能够用来描述局部的特征, 而微观无穷大又给了这个方程成立的条件, 即提供了统计上的意义.

然后是两个应用, 分别对应着上图中的 $\varepsilon \rightarrow 0$ 和 $\varepsilon \sim 0$. 具体的解释见下:

Hillbert Expansion ($\varepsilon \rightarrow 0$)

Hillbert 将这个方程通过展开的方式来忽略 $\varepsilon$ 的影响, 即达到 $\varepsilon \rightarrow 0$ 的目的.

\[f^{\varepsilon}(x, t, v) \sim \sum_{k=0}^{\infty} f_k(x, t, v)\]

( 这样的展开有点像是泰勒展开, 也有点像是物理里面的渐进摄动的操作. )

于是这个时候, 就可以通过考虑 $\varepsilon$ 的不同的阶数来重新考虑之前的方程了. 比如最低阶的 $\varepsilon^{-1}$ 的时候, 对应的方程就会写作 $0 = Q(f_0, f_0)$. 其解满足 Local Maxwell Distribution.

Chapman-Euskog Expansion ($\varepsilon \sim 0$)

这个时候的展开如下:

\[f^{\varepsilon}(x, t, v) = \mu^{\varepsilon}_f(t, x, v)(1 + \sum \cdots)\]

这个公式当时一闪而过, 也没怎么仔细抄完, 回过来到网上找, 感觉也总是有点不像, 但是公式是什么没有什么必要, 简单来说就是这个新的展开并没有将 $\varepsilon$ 抛掉, 仍然是考虑了 $\varepsilon$ 的作用.

所以这样的展开重新放回到原本的方程中后, 还能够保证在方程中考虑 $\varepsilon$ 的影响.

目前的方向

边界

好像没有怎么展开讲…

是否又光滑解, 或者说, 处理奇异解, 即激波的问题

奇异解本来应该是一种不光滑的解, 但是用来描述这个解的方程却是一种微分方程. 也就是说, 这个解仍然会有一个导数…

( 注: 突然想到我的一个大佬同学( 想搞图形学 ), 在微积分课程结束后快乐地大喊: “以后就是天王老子来了我也不会证明一致性的. 随便数学家怎么鄙视我, 反正从此刻起我可以想求导就求导想积分就积分并且想xjb换序就xjb换序了, nice! “ 乐, 让我们随意求导吧, 让数学家再去担心这些乱七八糟的数学操作是否有效吧. )

呃, 不嘴瓢了. 不光滑的解却仍有导数, 这个操作可以通过广义函数的方式来解释. 比如说常见的 $\delta$ 函数, 可以通过 Schwarz 分部函数理论来解释 ( 大概 ).

又或者是老师举的 Burger Equation 的例子:

\[u_t + (\frac{1}{2}u^2)_x = 0\]

其会产生一个 Shock Wave 的解:

\[u^s(x, t) = \left\{\begin{array}{ll}U_{-} & x < st\\ U_{+} & x > st\end{array}\right.\]

这里可以看到一种分部函数的样子, 我想就是因为像这样的分部函数, 所以导致了连续性的缺失, 于是刺激了数学家们想要着一个好的解决方法来解释这样的问题.

一个简单的想法可能是: 分部函数什么难的, 小学生和初中生不都会么? 只要将每一段都分别计算, 然后拼接起来不就好了. 但是困难的地方应该是这样的: 假如还是以前面那个飞机的图为例, 激波就应该是一个会移动的解, 也就是 $st$ 会变. 那么想要得到一个好的解, 就可能意味着要对每一个时间点对应的 $st$ 都要重新计算. 于是就会产生极大的计算量… ( 计算机没准可以… 但是这一点都不数学. )

而以 Bernhard Riemann 的一个方法, Riemann 在 1860 年的时候, 对 PDE 进行了研究, 其中一个部分就是研究了在 $1-D$ Eular Initial Data ( 1 阶 Eular 初始条件 ) 下, 上面的 (Burger Equation) 的计算方法.

$1-D$ Eular Initial Data, 可能就像是下面这样:

\[(\rho, u, \theta)(x, 0) = \left\{\begin{array}{ll} (\rho_{-}, u_{-}, \theta_{-}) & x < 0 \\(\rho_{+}, u_{+}, \theta_{+}) & x > 0 \end{array}\right.\]

可以看到就是一种分部函数…

而 Riemann 方法的一个思路就是: 若 $u(x, t)$ 是其中的一个解, 那么 $u_{\lambda}(\lambda x, \lambda t)$ 也是其中的一个解, ( 体现了一种伸缩不变性的感觉. ) 那么就可以将方程降维变为 $u(\frac{u}{t})$.

这个解的一个直观的例子就是, 假如在空中吐出一个烟圈, 这个烟圈在一定的时间里面, 就像是会保持形状不变, 但是逐渐向外放大的感觉. ( 注: No Smoking. 如果真的有这个兴趣的话, 可以去 b 站上搜索一下烟圈枪, 或者去搜索维基百科上的 Smoke Ring 的词条. )

于是有了这个技术方法, 就可以用来求解逼近解. 相应的方法, 也可以被计算数学, ( 乐, 鄙视链了属于是 ), 来使用 – 比如比较成熟的 Riemann 解算器. 这样的方法, 也能够得到下面的一个情况 ( BV solutioin by Reimann Solver)

BV ( 有界变参函数 ) $f’ \in \mathbb{L}^1$ 的解

这里老师讲得不是很详细, 或者是因为我摆烂了… 只记了老师讲的一个历史小故事.

在 1965 到 1970 年, Glimm 提出了一种解法 ( Glimm 格式 ). 但是, 当这份成果终于远渡重洋, 来到中国的时候, 大部分在数学所的老师们都在 五七干校劳动改造. 恰好老师的导师当时幸运地看到了这份文章, 于是很是高兴, 立刻抄写了一遍, 回去后就每天在劳动的过程中去思考, 在地上以 “设计铁锹” 的名义涂涂画画…

$\mathbb{L}^{\infty}$ 中的弱解

太难了, 就跳过了.

一些应用 – 鸟群和鱼群等环境中的应用

这一段我认为可以这样说: 用这样的方法来应用到集群的问题中去. 虽然很早就有类似的说法: Birds of a feather flock together.

于是为了解释这个现象, 一个叫做 The Cucker-Smale Model 被提了出来:

\[\frac{\mathrm{d}x_i}{\mathrm{d}t} = v_i, \frac{\mathrm{d}v_i}{\mathrm{d}t} = \frac{K}{N} \sum \psi(\vert x_j - x_i \vert)(v_j - v_i)\]

其中, $\psi(\vert x_j - x_i \vert)$ 为 C-S communication rate ( 关系函数 ), 为 $\psi(\vert x_j - x_i \vert) = \frac{1}{(1 + \vert x_i - x_j \vert)^{\beta}}$. 其中 $\beta$ 为一个 $\geq 0$ 的常系数.

这个公式的话, 用一个简单的理解就像是一堆粒子之间, 考虑相互作用的形式与距离有关, 距离越远, 作用越小; 且相互作用与速度也有关系… 于是最终的结果就会发现, 这样的解会产生一种积聚的效应 – 也就是物以类聚的特征.

甚至, 可以继续拓展, 比如在每个粒子之间加入不同的权重因子, 可能就会产生更多不同的结果. 感觉还是挺有意思的.

后记

大概以后听到有意思的讲座都会做一点这样的笔记. 嘛… 不过手上还堆着好多没写完…