Make A Turing Machine Yourself

Make A Turing Machine Yourself

What’s Turing Machine?

Purely formally a Turing machine can be specified as a quadruple $T = (Q, \Sigma, s, \delta)$ where:

• $Q$ is a finite set of states $q$
• $\Sigma$ is a finite set of symbols
• $s$ is the initial state, $s \in Q$
• $\delta$ is a transition function determining the next move:
  \(\delta : (Q \times \Sigma) \rightarrow (\Sigma \times \{L, R\} \times Q)\)

The transition function for the machine T is a function from computation states to computation states. If $\delta (q_i, S_i) = (S_{i, j}, D, q_{i, j})$, then when the machine’s state is $q_j$, reading the symbol $S_j, T$ replaces $S_j$ by $S_{i, j}$, moves in direction $D \in {L, R}$ and goes to state $q_{i, j}$.

Turing Machines form Stanford Encyclopedia of Philosophy

Note: there are also a similar but little different formal definition.

I won’t cover much of the history about Turing Machine, so if you like, please refer to the wiki for its history.

呃, 看起来也许有一种不明觉历的庄严感, 但是实际上图灵机(Turing Machine)是一种非常简单的计算机模型.

(注: 这个简单更应该说是结构简单. 但是虽然结构很简单很基础, 但是并不代表给它编写程序会是一种让人愉悦的事情. 我不会强调和注重编写程序的效率和速度之类的东西, 毕竟这些还是交给计算机系的人来卷吧. 我们的目标就是能动的图灵机! )

先把图灵机形式化的定义扔到一边

(假如你觉得图灵机的形式化定义非常容易理解的话, 那么还是直接跳过看看代码的实现吧. 因为我觉得代码就足够具有表现力了. )

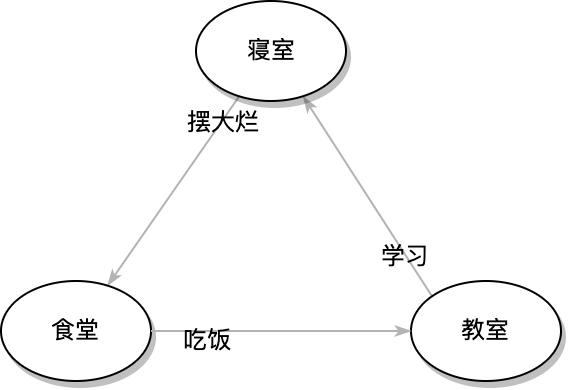
三点一线的生活

我记得曾经有一种非常文艺地表现自己生活单调贫瘠的说法: 宿舍 - 食堂 - 教室, “三点一线的生活”. 这里就体现了一个过程: 从一个状态变化到下一个状态. 每一个状态下都会执行相应的动作. 做完了动作就会移动到下一个状态.

虽然不愿意这样说, 但是这样的生活就是一种简单的”计算机”. 稍微用形式化的书写来表达就是:

宿舍: 摆大烂 -> 食堂
食堂: 吃饭   -> 教室
教室: 上课   -> 宿舍

我们会发现, 将我们的状态首尾相接, 就组成了一个类似于环状的结构. 于是就像是土拨鼠之日一样, 我们就处于一个循环的状态.

All Works And No Play…

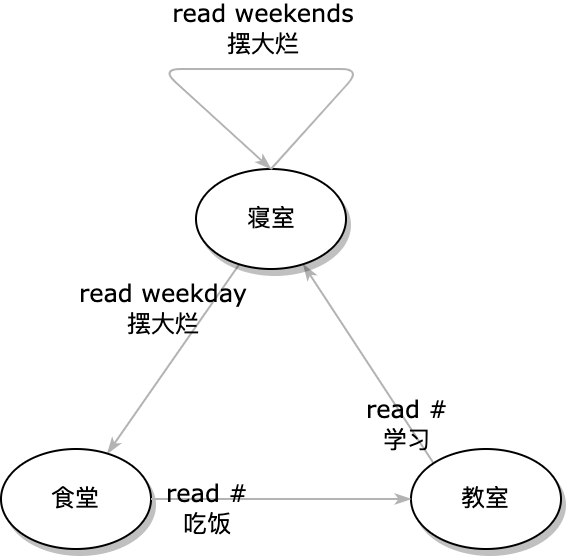
但是除了上课, 我们实际上还有放假啊. 假如说每天你在宿舍里都会检查一下今天的日程表, 假如期盼的假期终于来到, 那么你就打算一直在宿舍里面摆大烂. 除非你的美好假期在光影如梭中消失不见.

这个时候, 我们做了一个读取信息的操作. 于是上面的故事就需要稍微修改一下了: 在寝室, 读取日历, 如果是”weekends”, 就在寝室一直摆烂; 如果是”weekdays”, 就去食堂… 那么形式化的写法就是:

寝室, read weekends: 摆烂 -> 寝室
寝室, read weekdays: 摆烂 -> 食堂
食堂, read #: 吃饭   -> 教室
教室, read #: 上课   -> 宿舍

(其中为了格式一致, 我们在原来的食堂和教室后面也加上了read的标志. )

这个时候, 我们就相当于实现了一个条件判断. 在原来的基础上, 我们通过条件的分支在原来的基础新加入了一个循环(双循环可还行).

开始与结束

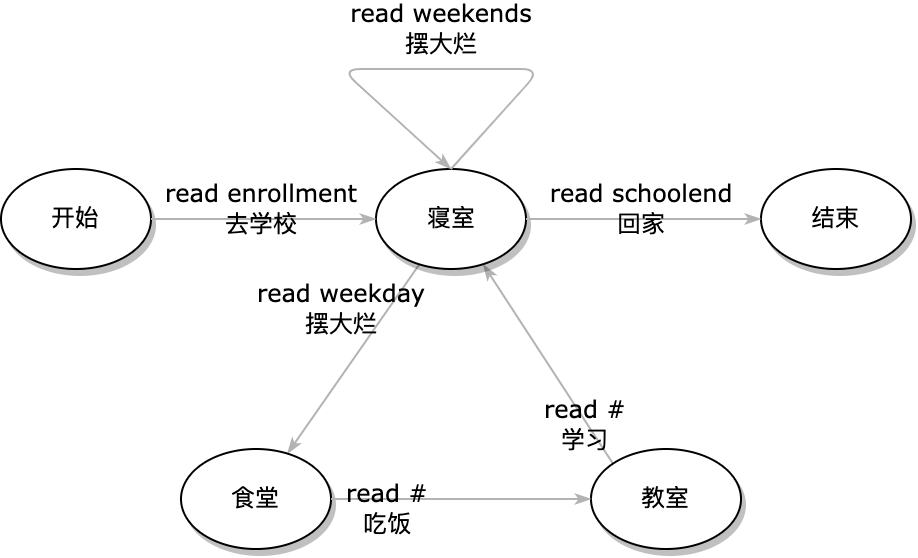
其实我们的人生并不是这么可怕的土拨鼠之日的循环的, (像这样的无限循环能否迎来终结之日的问题, 叫做图灵停机问题, 比如说是Alan Turing为了研究哥德尔不完备性定理想出的一个东西. 这里我们就不必这么高大上地介绍了. ) 一件合理点的事情, 总该是有开始, 也总该是有结束的. 同理, 我们的”计算机”也应该有开始和结束.

让我们加入一点点的新的状态:

开始(开学), read enrollment: 去学校 -> 寝室
寝室, read weekends: 摆烂 -> 寝室
寝室, read weekdays: 摆烂 -> 食堂
寝室, read schoolend: 回家 -> 结束
食堂, read #: 吃饭   -> 教室
教室, read #: 上课   -> 宿舍

请思考这两个状态有什么用. 我不会告诉你我在图片上面加了一个注释, 里面写了一些我自己的理解的.

那么能不能把你做了什么说得更加清楚一些呢?

其实上面我做了什么实在是有点, 怎么说呢, 太抽象了. 假如计算机能够理解的话, 估计人工智能系的那帮人要肝好久了. 那么我们就写得详细一点吧:

什么是摆烂呢? 就是在日程表上写下”时光飞逝, 我在摆烂”, 然后看着时间流逝把你的日程表从此刻拨到下一刻:

寝室, read weekends: write "时光飞逝, 我在摆烂", move next_schedule -> 寝室

那么这个时候, 我们相当于就已经实现了一个”完整”的图灵机了. 虽然格式不太严格, 但是总归来说还算是该有的都有了. 那么总结一下:

• 我们的所有操作都是在一个”日程表”(或者也可以叫纸带什么的)上进行的
  • 我们可以从日程表上读取read数据
  • 我们也可以在日程表上写入write数据
  • 在每次操作(读和写)后, 我们可以选择在日程表上移动, 也就是对应着一个日程表上的位置.
• 我们操作以及操作的规则是由我们的状态和读取的规则来确定的, 就好像是在寝室这个状态, 读取到的weekends的数据, 就决定了我们的write和move的具体的行为.

那么假如我们想要制作一个图灵机, 我们只需要制作一个能够按照规则, 从纸带上读取, 写入, 移动, 然后转换状态的机器即可.

用Ruby制作一个图灵机

为了简单, 我们将会把上面的例子里面的图灵机做一个简化, 把命令形式改写成如下形式:

状态, 读取, 写入, 移动, 下一个状态

并且限制我们的图灵机每次只能够读取和写入1个字符. (就是为了体现一个未经世事的图灵机的感觉. )

读取并识别规则集

我们肯定希望能够每次读取一个已经写好的规则(因为怎么说呢, 图灵机的规则输入还是挺麻烦的, 最好是能够保存在一个文本文件里面, 然后每次载入一个规则集. )

那么我们就写一个读取的函数:

def read_file(path)
  # 返回的指令集为 instructions
  instructions = {}
  # 读取文件的每一行
  File.open(path).each_line do |line|
    # 去掉空白符和换行符
    line = line.strip.gsub(" ", "").split(",")
    # 只选择符合条件的命令输入
    if line.length == 5
      # 多赋值, 只是一个小技巧而已
      key, sub_key, *value = *line
      # 初始化状态
      instructions[key] = {} unless instructions[key]
      # 写入读取的规则
      instructions[key][sub_key] = value
    end
  end
  # 返回处理过后的数据
  return instructions
end

假如我们讲读取的规则储存在instructions = read_file("code.txt")中, 这样我们就可以通过write, move, next_state = instrcutions[state][read]这样的方法来读取写入的数据, 移动的方向和下一个的状态名称了.

执行机器

我们不妨设计这样的一个机器, 它初始化的时候, 处于"q0"状态, 也就是我们的开始状态. 初始化的时候会读取一个规则集. 然后初始化的时候, 我们会有一条纸带. (这里不妨设纸带一开始就是空的).

class Machine
  # 新建一个图灵机, 默认纸带为空
  def initialize(path, string = "")
    # 规则集
    @instructions = read_file(path)
    # 初始化
    set(string)
  end

  # 设置纸带上原本就有的内容, 初始化
  def set(string)
    # 初始状态为 "q0"
    @state = "q0"
    # 初始在纸带上的位置
    @head = 0

    @strings = {}
    # 将纸带写成{:"0" => "B", :"1" => "B"}的形式
    # 如果输入是空的话, 就变成不处理了
    string.length.times.each do |i|
      @strings[i.to_s.to_sym] = string[i]
    end if string != ""
  end

  # 从文件中读取规则集
  def read_file(path)
    # ...
  end
end

注意到上面我们定义了纸带的储存方法, 我们定义假如纸带上读到了没有写数据的地方的话, 就返回一个特殊字符叫做"B", 这个字符可以表示这里什么也没有. 于是我们就可以构造read和write命令. 不过先把这个东西放在一边, 我们先构造一个最基本的规则实现的函数吧:

def step
  # read() 返回 @head 所在的位置的 @strings 上的数据
  write_char, move_to, @state = *(@instructions[@state][read()])
  # write(char) 会在 @head 所在的位置写入 char
  write(write_char)
  # move_to(forward) 会根据 forward 来移动 @head
  move(move_to)
end

然后我们根据上面的规定来写出一点点的读写代码:

def read
  # 把 @head 转换为 @strings 中的标签
  head = @head.to_s.to_sym
  # 假如没有数据, 就是 "B"
  if @strings.include? head
    return @strings[head]
  else
    return @strings[head] = "B"
  end
end

def write(char)
  @strings[@head.to_s.to_sym] = char
end

def move(forward)
  # 只有两种移动方式, 向左, 向右, 否则就报错
  if forward == "L"
    @head -= 1
  elsif forward == "R"
    @head += 1
  else
    raise "Error when moving! "
  end
end

于是我们就完成了最基本的图灵机的部分了.

在irb中尝试一下, 其中的code.txt里面是一个将等号前面所有的1移动到等号后面的一个图灵机程序, (虽然我们课上叫它一进制加法, 乐).

其中, 我们的图灵机代码储存在"main.rb"里面, 而我们的"code.txt"里面是一个将等号前面所有的"1"移动到等号后面的一个图灵机程序, 虽然我们课上叫它一进制加法, 乐. (点击展开查看)

q0, +, +, R, q0
q0, =, =, R, qa
q0, 1, e, R, q1
q0, E, E, L, qa
q1, 1, 1, R, q1
q1, +, +, R, q1
q1, =, =, R, q1
q1, B, 1, L, q2
q2, 1, 1, L, q2
q2, +, +, L, q2
q2, =, =, L, q2
q2, e, 1, R, q0

3.0.0 :001 > load "main.rb"
 => true 
3.0.0 :002 > m = Machine.new "code.txt", "11+111="
 => #<Machine:0x0000000120866138 @instructions={"q0"=>{"+"=>["+", "R", "q0... 
3.0.0 :003 > m.step
 => 1 

坏了, 我们忘记了给这个东西写一个漂亮的输出了!

现在补救还来得及, 但是既然准备上手了, 为什么不试试看给它来点高级的功能呢?

高级代码, 点击就送. (啊, 999999!!!! 你砍了我好多刀啊. )

# step 的缩写, 是带有输出的step
def s
  step()
  puts output()
end

# 输出一个字符串
 def output
  # 防止 @head 在的地方什么也没有, 
  # 所以先读一次, 至少写一个 "B" 进去
  read()
  # 输出 @head 头的位置
  num = 0
  # 输出的值
  res = ""
  # 按照 key 的数值大小来排序
  @strings.to_a.sort_by{|item| item[0].to_s.to_i }.each do |item|
    res << item[1]
    # 找到了 @head 头的位置
    num = a[0].to_s.to_i if a[0].to_s.to_i == @head
  end
  # 输出一个指向符号, 也就是 @head 在的位置
  res << "\n" + " " * num + "^"
end

# 运行, 通过设置speed来调整速度
def run(speed = 1)
  interveral_time = 1.0 / speed
  while @state != "qa"
    s()
    sleep interveral_time
  end
end

# 运行直接到结束, 但是只在最后一次输出
# debug 来选择是否每次输出
def finish(debug = false)
  debug ? s : step while @state != "qa"
  puts output
end

重新在irb里面载入代码:

3.0.0 :004 > load "test.rb"
 => true 
3.0.0 :005 > m = Machine.new "code.txt", "11+111="
 => #<Machine:0x0000000115847d38 @instructions={"q0"=>{"+"=>["+", "R", "q0... 
3.0.0 :006 > m.s
e1+111=
 ^
 => nil 
3.0.0 :006 > m.finish
 => 
11+1111=111111
        ^ 

为了让这个程序看起来更加好一点, 你可以做一些更多的事情, 比如修改inspect之类的方法等等… 就是你的喜好啦.

(又, 为了防止你照抄我的代码, 我在我的Ruby代码里面留了一些小错误. 其实是一开始直接在markdown里面写代码, 运行的时候调了调, 忘了自己有没有改过来了. 不过我不管, 这就算是检查你学没学会把. 乐.)

What to do next?

这个东西我还会继续写, 不过现在我将会结束这一部分了. 接下去我会介绍如何构造图灵机的代码, 以及如何将这个黑乎乎的命令行的玩意儿放到网页上. (虽然前面的例子里面就相当于是一个如何构造的例子了. )

OK, Update! Let’s do some coding…

其实我觉得叫做coding, 其实有点名不副实, 因为code在英文里面的的解释更像是加密或者编码. 尽管某种程度上来说, 又臭又长的代码看起来确实人人迷幻, 给人一种加密的感觉. (误)

a system of words, letters, or signs used to represent a message in secret form, or a system of numbers, letters, or signals used to represent something in a shorter or more convenient form.
cambridge dictionary

好吧, 不扯淡了. 其实编写程序的时候, 我们更像是通过一些方法来将我们对过程的描述通过特定的方式编码成计算机能够理解的形式. 那么如何才能够将过程”轻松”地转换成计算机程序呢?

我们会用到的简单的形式

直线

据说恐龙都是单线程的动物, 它们一次只能够执行一件事情. 追着猎物, 抓到猎物, 吃掉猎物, 排泄… 啊. 其实我们也可以用图灵机来实现这样的事情, 即编写一个单线程的程序. 而我们所要做的不过就是从一个状态变为另一个状态, 最后结束. 仅此而已.

state A -> state B -> state C

那么举个例子, 我们现在想要在纸带上输出一个字符串: “Lucky_Me!”, 那么我们思考一下, 现在需要做什么? 答案是先写一个”L”, 再写一个”u”, 然后如此继续直到写下”!”结束. 所以很容易构造出其所对应的过程.

点击查看答案代码.

q0, B, L, R, q1
q1, B, u, R, q2
q2, B, c, R, q3
q3, B, k, R, q4
q4, B, y, R, q5
q5, B, _, R, q6
q6, B, M, R, q7
q7, B, e, R, q8
q8, B, !, R, qa

并且, 其实你会发现这样的过程是非常容易形式化地去描述的, 也就是说, 如果我们想要生成这样的代码的话, 只需要:

def turing_machine_print(str)
  str.length.times do |i|
    puts "q#{i}, B, #{str[i]}, R, q#{i < str.length - 1 ? i + 1 : "a"}"
  end
end

(其实上面的代码就是这样生成的. )

并且我们可以在直线的基础上加入一些分支, 这样就可以做到条件判断的方式了.

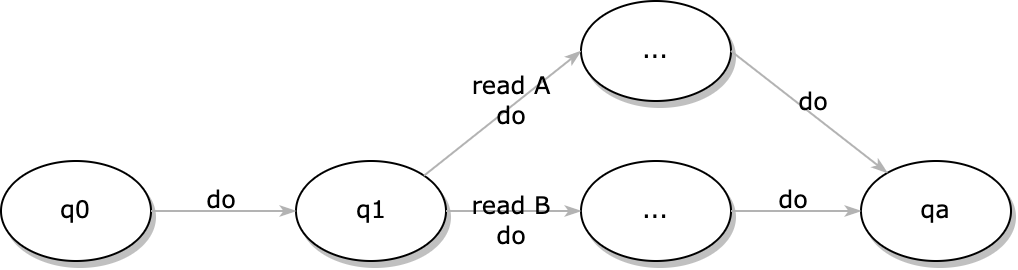
举个例子, 假如我们有一个想要一个能够根据提前设置的纸带上的内容来格式化输出东西的程序. 比如一开始的纸带上的内容上的内容是”bBbBbbbBB”之类的, 然后我们输入的是”lucky”, 如果看到”b”的话就用大写来输出, 如果是”B”, 也就是什么也没有的话, 就用小写来输出.

来试试看吗?

def condition_print(str)
  str.length.times do |i|
    puts "q#{i}, B, #{str[i].downcase}, R, q#{i < str.length - 1 ? i + 1 : "a"}"
    puts "q#{i}, b, #{str[i].upcase}, R, q#{i < str.length - 1 ? i + 1 : "a"}"
  end
end

环形

据说fushojo们特别喜欢那些掰弯的情节… 我们不妨为了迎合受众, 来点喜闻乐见的情节: 把上面的状态图给”掰弯”, 然后收尾相接, 那么我们就得到了一个环啦!

(诶, 讲一个题外话, 突然发现, 如果把单位元的一次运算看作是在图灵机的状态从一个状态转移到下一个状态. 那么一个环, 比如$\mathbb{Z}/p\mathbb{Z}$就像是一个有$p$个元素组成的大致结构和上图类似的环. 而$\mathbb{Z}/p_1\mathbb{Z} \cup \mathbb{Z}/p_2\mathbb{Z}$则有点像是两个有交点的环的结构. 嗯, 鉴定完毕, 可以用代数来处理了. 那么来吧, 伟大的代数学家们! 我跑路了. )

但是只是简单的一个环其实还是不太行的. 假如一直在一个环上运转, 那么不就像是陷入了无穷的循环了吗? 所以我们还是需要结束的方式, 来从这样的无限循环中解脱出来.

这里举一个例子. 假如我们想要在一个能够按照输入来重复填充东西的程序. 比如说输入是”bbbbbbbbbbbbbbb”(15个”b”), 然后我们要用”lucky”重复填充. 那么是不是相当于就只要反复地输出”lucky”, 即执行同样的代码一次一次又一次… 那么思考一下:

来看看?

def multi_print(str)
  str.length.times do |i|
    puts "q#{i}, b, #{str[i]}, R, q#{i < str.length - 1 ? i + 1 : "0"}"
    puts "q#{i}, B, B, L, qa"
  end
end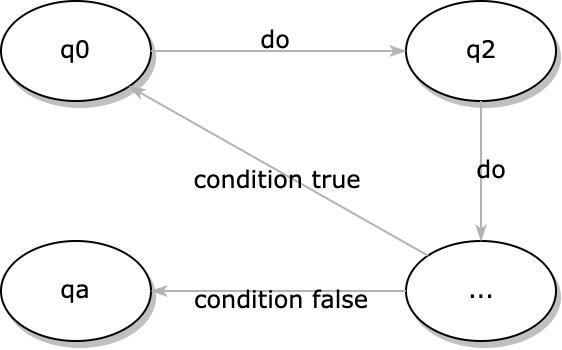

寄存器(其实并不是什么新的东西, 只是我觉得很有意思所以写了上去, 因为是我自己想到并且命名的. 总是要有点成就感的吧… 欸, 标题不应该写这么长的. 23333)

其实这个不过是条件分支的一些花里胡哨的用法啦. 我们可以通过不同的状态来储存信息, 然后通过在状态之间的不断切换来达到一个内存的保存的功能. 举一个例子, 假如我们想要把纸带上的内容向右移动一格, 在原来的地方写上新的东西. 假设纸带上的字符集为”0”, “1”. 那么我们现在想要写下一个零, 然后把原来的东西全部向右移动:

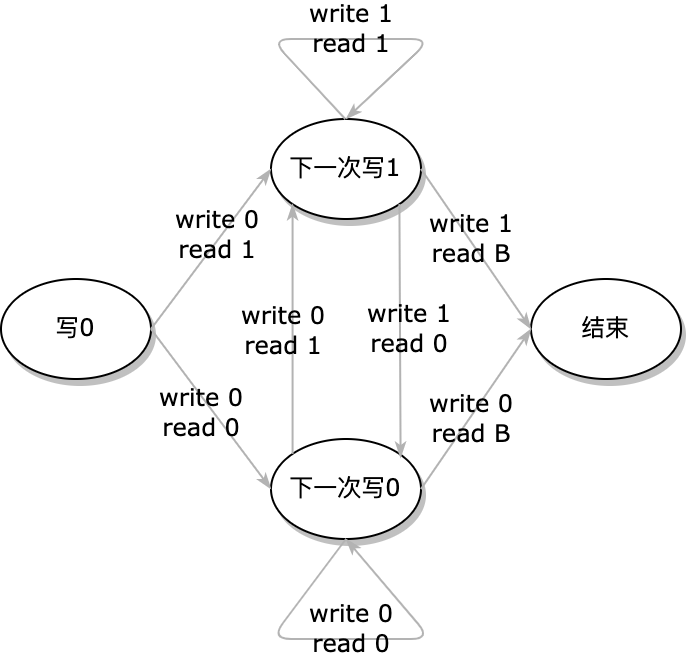
那么, 如果我们将其扩张为任意字符集...

def shift_right(write, charset)
  charset.each do |c|
    puts "q0, #{c}, #{write}, R, qc#{c}"
  end
  charset.each do |c|
    charset.each do |next_c|
      puts "qc#{c}, #{next_c}, #{c}, R, qc#{next_c}"
    end
    puts "qc#{c}, B, #{c}, R, qa"
  end
end

这样的话, 假如你想要一个负数, 就只需要执行一段`shift_right("-", ("0".."9").to_a)`代码就能够自动生成相应的代码了.

(这个结构是我从电路里面的寄存器得到的相应的启发. 不过不知道有没有人早就想过了. 嘛, 不管它了. )

我们会用到的简单技巧

化抽象为具象

尽管图灵机只能够做到读取一位, 写入一位, 移动的简单的操作. 相当于我们能干的事情被具体化限制到了非常狭隘的具体的一个区域里面. 我们如果想要做一些非常”抽象”的操作的时候, 就会让我们感到十分吃力. 因为我们可能没办法立刻把我们平时习以为常的一些操作一下子变成图灵机的操作.

但是没关系, 我们可以用一种叫做逐步具象的方式来构筑我们的程序. 也就是说, 我们的思路大概是这样的: 人是一个整体, 但是整体里面有各种的部分, 不妨拿脑子为例, 脑子是人的身体的一部分. 这个时候, 我们就完成了一次分解. 然后脑子其实还可以被分解成大脑, 小脑, 脑干, 这样我们又完成了一次分解. 然后大脑可以分解成一些中枢… 最终分解成细胞, 分子, 原子… 最后我们面对了一堆基本粒子. 这个时候, 这些基本粒子, 不论他们是否能够分解, 我们已经都已经到了一个不需要继续分解的地步了.

(这个时候我们不妨讨论一下”取一杆, 日折其半, 百世不竭”还是”终有一尽”的问题了吗? 哈哈, 不必要这样吧… 因为我认为计算机像是一种约定主义, 我们已经约定了最小的计算单元, 所以假如可以分解的话, 我们应该是能够分解的. 但是假如是一种无法分解的东西, 比如 “这种东西的分解是那样的东西, 使得其的分解就是这种东西本身…” 坏, 别认为这东西只是数学废话啦. 我记得罗素悖论里面也有类似的东西. )

举一个例子, 假如我们想要做一个按位异或的程序, 并且假设输入的纸带类似这样: “0101^0011=”, 也就是左右等长的呢.

那么我们不妨思考一下, 这个问题可以如何分解: 什么是按位异或? 那么只需要每次取一位, 然后将其运算的结果写入即可. 于是过程初步分解为: 取第一个数的第一位 -> 取第二个数的第一位 -> 在最后写入计算的结果 -> 回到开头 -> 取第一个数的第二位 -> … -> 取第n位…

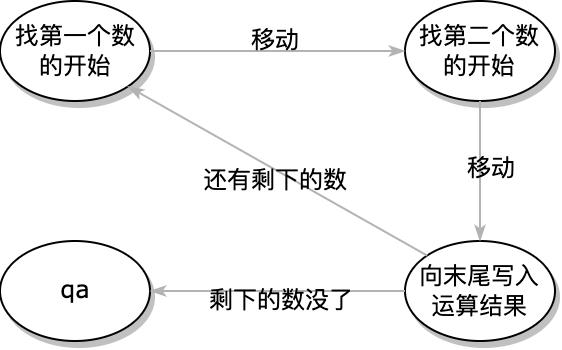
于是我们只需要思考如何能够实现里面的每一个小步骤即可了. 以取第一个数的第一位为例: 我们一开始就位于纸带的开头, 也就是第一个数的可能的位置, 但是当我们做了操作之后, 第二个数才是要被读的东西… 既然我们的图灵机可以做标记, 那么不妨我们使用标记的方式来达到这个目的. 于是这个找到第一个数的方式就变成了一个条件分支:

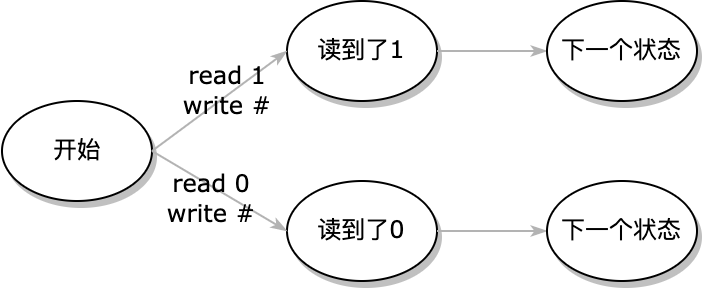
化具象为抽象

其实除了分解, 我们也能够通过组合的方式来构造一个宏大的程序.

(很多时候, 这样的构造方法其实也是非常的简单的构造方法. 只要把过程按顺序连接在一起就能够合成一个新的大的过程. 然后因为我们构造了这样的过程, 我们只需要知道其根据输入会有怎么样的输出, 就可以用黑箱方法, 不必要计较内部的具体实现. 这个时候, 就相当于是一种对过程的抽象调用了. )

方法是这样, 那么实际应用的时候其实也差不多就是这样. 那我就不介绍啦, 读者自证不难…

一个例子

假如我们要实现一个从任一状态出发, 滚动到纸带最开头的代码. 然后调用一个状态. 那么我们可以这样设计:

def roll_to_empty(q_start, q_end, charset, forward = "L", end_char = "B")
  charset.each do |c|
    puts "#{q_start}, #{c}, #{c}, #{forward}, #{q_start}"
  end
  puts "#{q_start}, #{end_char}, #{end_char}, #{forward == 'L' ? 'R' : 'L'}, #{q_end}"
end

于是我们不妨设置这样的一个过程: 先让我们移动到纸带末尾, 然后移动到纸带开头.

roll_to_empty("q0", "q1", ["0", "1"], "R", "B")
roll_to_empty("q1", "qa", ["0", "1"], "L", "B")

优化, 简化, 美化, debug等等

呃, 其实怎么说呢, 对我来说, 美化比优化和简化可能更加重要一些. 毕竟我是一个无聊的人. 并且其实这些方法也不是和上面的方法独立的方法, 所以我就把它们和在一起介绍了.

(这并不是说它们不重要啊, 只是我懒得写了, 嘛, 这不就像是一本合理的教材一样嘛: 例题结论简单普适, 习题考题却是巨难无比. 突然想起离散数学的老师讲的一句话, 搞数学的这帮人总是喜欢简单的东西, 他们在自己脑子里面举的例子大概的规模就是1, 2, 3. 所以他们脑子里面很清晰. 但是搞计算机的人就很苦逼, 因为他们面对的都是双十一的服务器的工作量的级别的关系. )

• 优化与简化: 其实就是想方法把原本的过程进行简化, 让它跑得更快一些, 或者用的状态数更少一些. 这个时候奇技淫巧就很多了, 但是我比较笨, 所以不太会.
• 美化: 其实美化有时候会导致程序变得更加复杂. 但是这并不是一个非常难以忍受的事情. 比如苹果的设计和其对性能的影响…
• debug: 其实debug的过程在编写代码的时候就已经开始了.
  在编写代码的时候, 我们可以在边上留下注释, 这样就可以方便后期的回看和调试. 毕竟知道了本来应该干什么, 但是却不像原来应该干的那样干了. 显然就是那一块出现了问题. (当然, 也有可能是前面或者后面的哪里出了错, 但是人总是懒惰的, 先检查一个点和先检查一个面相比, 肯定是前者啊. )
  假如找到了bug, 想要修改程序, 与其推倒重来, 不如就在原本的基础上进行修改. (不过这样可能就要求你原本的程序有比较好的结构和分块. )

接下去搞什么?

接下去… 我有几个无聊的想法:

• 能不能像之前的りlang一样, 为图灵机制作一门高级语言, 毕竟哪怕上面我已经介绍了这么多方法, 实际人来构造的时候还是挺麻烦的.
• 能不能做一个图形化的状态图编辑程序, 比如在线画状态图, 然后一键导出图灵机代码
• 能不能做一个可视化的图灵机状态转移图
• …

不过, 还是先放着吧. 以后再来.