About

想要了解更多的一些关于 “函数式” 的知识, 毕竟每次看到网上有人讲到函数式就是范畴论起手, 让我这种对函数式的浅薄印象只停留在 “不可变数据结构”, “函数一等公民” 这样的菜逼十分的担忧, 思来想去还是得学点硬的.

这本书是看到网上有位 55 岁退休闲得慌的大哥推荐的 (推荐的 网页, 英文版, 不过其实感觉更像是读书笔记, 虽然大哥的笔记真强 什么日本人刻板印象).

(大哥的自述 原文: “2014年に５５歳で退職しました．早まったかもです．”)

并且这本书 (Basic Category Theory) 的作者免费把书开放在了 arXiv 上: Tom Leinster : Basic Category Theory, 2014 (https://arxiv.org/abs/1612.09375).

(真是好人啊)

为了防止我鸽了, 采用一天一更新的方式进行一个记录.

记录的内容
  • 原文中的 Example, Exercise, Lemma, 保留原文的标号

+

Introduction

Example 0.1:

  • 符号 \(1\) 用于表示 只有一个元素的集合.
  • 性质: 任意 集合 \(X\), 存在 \(X → 1\) 的映射.
  • 符号 \(→\) 用于表示映射 (map, mapping, function)

Example 0.2:

  • 性质: 任意 环 (ring) \(R\), 存在 唯一 (unique) 同态 \(\mathbb{Z} → R\)
  • 证明:
    略
    • 存在性:

      \[φ(n) = \left\{ \begin{matrix} \underbrace{1 + \cdots + 1}_{n} & \mathrm{if}\ n > 0 \ 0 & \mathrm{if}\ n = 0 \ - φ(-n) & \mathrm{if}\ n < 0 \end{matrix} \right.\]

    • 唯一性:

      \[ψ(n) = ψ(\underbrace{1 + \cdots + 1}_n) = \underbrace{ψ(1) + \cdots + ψ(1)}_n = \underbrace{1 + \cdots + 1}_n = φ(n)\]

      注: 这里用了同态的线性, 反证法证明之; \(n = 0\) 用同态的零元; \(n < 0\) 同理.

Lemma 0.3:

  • 若对 任意 环 \(R\), 存在 同态 \(A → R\) (称该性质为 “initial”), 则 \(A ≅ \mathbb{Z}\)
  • 符号: \(≅\) isomorphism
  • 证明:
    略
    • \(A\) initial \(⇒\) 存在唯一 同态 \(φ: A → \mathbb{Z}\);
    • \(\mathbb{Z}\) initial \(⇒\) 存在唯一 同态 \(φ': \mathbb{Z} → A\);
    • 得 \(φ' ˆ φ = 1_A, φ ˆ φ' = 1_{\mathbb{Z}}\)

Example 0.4:

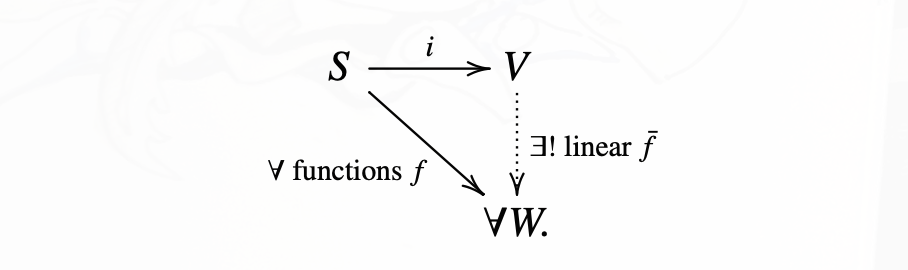
  • 矢量空间 (vector space) 的映射可以变成基底 (basis, \((v_s)_{s ∈ S}\)) 的映射.

    (specify a linear map from \(V\) to \(W\) simply by saying where the basis elements go)

  • 任何定义在基底元素的函数可以被拓展为 \(V\) 唯一的线性映射

    (any function defined on the basis elements exends uniquely to a linear map on \(V\))

    考虑函数: \(i: S → V, i(s) = v_s, s ∈ S\), 对 任意 函数 \(f\), 存在唯一 线性函数 \(\overline{f}: V → ∀ W\). (这里是不是理解得有点错误? )

  • 交换图

    /_img/reading/basic-category-theory/s-v-w-map.png

Example 0.5:

  • 对集合 \(S\), 通过 discrete topology \(D(S)\) (topological space), 任意从 \(S → X\) 的映射都是连续的.

    这里不理解的是 discrete topology (all subsets are open?), topological space 的概念, 为啥就连续了?

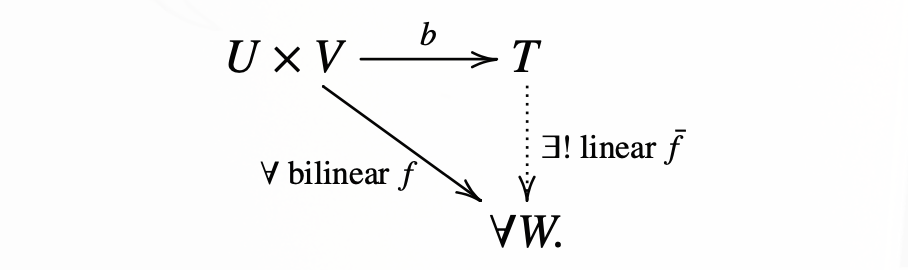
Example 0.6:

  • bilinear map \(f: U × V → W\) 满足:

    \[\begin{matrix} f(u, v_1 + λ v_2) & = & f(u, v_1) + λ f(u, v_2) \ f(u_1 + λ u_2, v) & = & f(u_1, v) + λ f(u_2, v) \end{matrix}\]

  • universal bilinear map: 一个 universal 的 bilinear map 满足以下交换图:

    /_img/reading/basic-category-theory/universal-bilinear-map.png

Lemma 0.7:

  • \(b: U × V → T, b': U × V → T'\), \(b\) 和 \(b'\) 是 universal bilinear map, 则 \(T ≅ T'\), 即 存在唯一 同构 \(j: T → T', j ˆ b = b'\).
  • 证明
    略

    交换图:

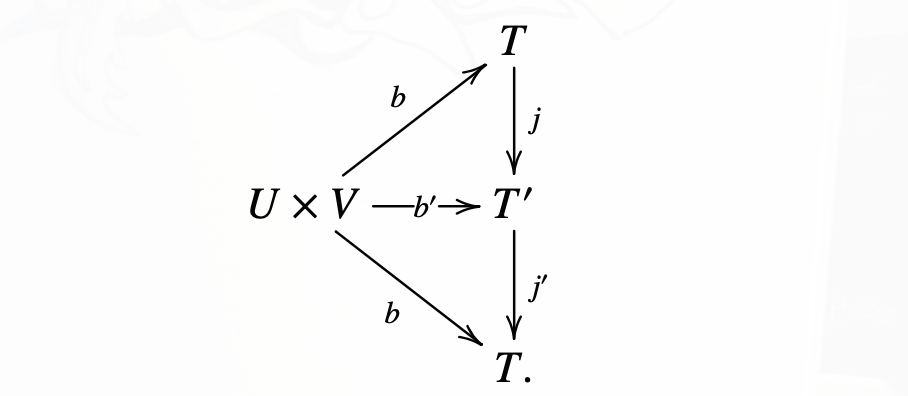
    /_img/reading/basic-category-theory/lemma-0-7.png

    相当于利用 Example 0.6 universal bilinear map 里面交换图, 固定 universal bilinear map \(b\) 和 \(∀\) bilinear \(f ⇒ b'\), 得到的 \(∃!\) linear \((\overline{f} ⇒ j, ∀ W ⇒ T') ⇒ j: T → T'\), 然后对称得到 \(j': T' → T\), 即构造了 \(1_T = j' ˆ j = j ˆ j'\).

    (所以交换图的作用就是来找路径咯? )

Example 0.8:

  • 令 \(θ: G → H\) 为一个群的同态, 有如下交换图:

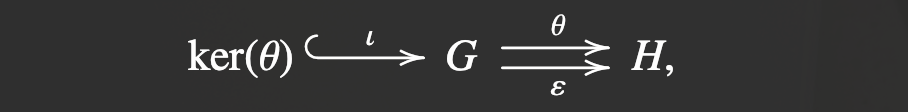
    /_img/reading/basic-category-theory/example-0-8.png

    其中:

    • \(\imath\) 是 \(\mathrm{ker}(θ)\) 到 \(G\) 的包含映射 (inclusion)

      包含映射 (inclusion): \(∀ x ∈ \mathrm{ker}(θ), \imath(x) = x\), 用符号 \(\hookrightarrow \) 进行表示 (\(⊂\) 和 \(→\) 结合).

    • \(ε\) 为 trivial homomorphism.

      trivial: \(∀ g ∈ G, ε(g) = 1\)

Example 0.9: …

Categories, functors and natural transformations

A category is a system of related objects. The objects do not live in isolation: there is some notion of map between objects, binding them together.

typical examples:

  • object: group, topological space;
  • map: homomorphism, continuous map

Categories

Definition 1.1.1: 一个 category (范畴) \(\mathcal{A}\) 包含:

  • objects (对象) 的集合 \(\mathrm{ob}(\mathcal{A})\);
  • 对于每个 \(A, B ∈ \mathrm{ob}(\mathcal{A})\), 一个从 \(A\) 到 \(B\) 的 map, arrows, morphisms 的集合 \(\mathcal{A} (A, B)\);
  • 对于每个 \(A, B, C ∈ \mathrm{ob}(\mathcal{A})\), 一个 composition 函数:

    \[\begin{matrix} \mathcal{A}(B, C) × \mathcal{A}(A, B) & → & \mathcal{A}(A, C) \ (g, f) & \mapsto & g ˆ f \end{matrix}\]

  • 对于每个 \(A ∈ \mathrm{ob}(\mathcal{A})\), 一个 \(A\) 上的单位元: an element \(1_{A}\) of \(\mathcal{A}(A, A)\), called the identity on \(A\)

有以下公理:

  • associativity: \(f ∈ \mathcal{A}(A, B), g ∈ \mathcal{A}(B, C), h ∈ \mathcal{A}(C, D), (h ˆ g) ˆ f = h ˆ (g ˆ f)\).
  • identity laws: \(f ∈ \mathcal{A}(A, B), f ˆ 1_{A} = f = 1_{B} ˆ f\)

Remarks 1.1.2 记号:

  1. 将:
    • \(A ∈ \mathcal{A}\) 记为 \(A ∈ \mathrm{ob}(\mathcal{A})\);
    • 函数的映射 \(f: A → B, A \xrightarrow{f} B\) 记为 \(f ∈ \mathcal{A}(A, B)\)

      也有记为 \(\mathrm{Hom}_{\mathcal{A}}(A, B)\), 或者 \(\mathrm{Hom}(A, B)\) 的情况, \(\mathrm{Hom}\) 表示 homomorphism (同态).

    • 函数的结合 (compose) \(g f\) 记为 \(g ˆ f\)
  2. 对一串映射的连接 (string of map):

    \[A_0 \xrightarrow{f_1} A_1 \xrightarrow{f_2} \cdots \xrightarrow{f_n} A_n\]

    可以用一个映射来代替:

    \[A_0 \xrightarrow{f_n f_{n-1} \cdots f_1} A_n\]

  3. 交换图的 commutes: 如果一个交换图中有两条从 object \(X\) 到 object \(Y\) 的通路, 则称该交换图为 commutes 的;
  4. 称 “collection” 为 “set” 是一种比较模糊的称呼, 用 “class” 理解可能会比较好;
  5. 若 \(f ∈ \mathcal{A}(A, B)\), 则 \(A\) 为 \(f\) 的 domain, \(B\) 为 \(f\) 的 codomain.

    在所有的范畴中的映射都对应有一个明确的 domain 和 codomain.

Examples 1.1.3: (categories of mathematical structures)

  1. set: 其 object 为集合, 对应的 map 即传统的映射;
  2. grp: 其 object 为群, 对应的 map 为群同态;
  3. ring: 其 object 为环, 对应的 map 为环同态;
  4. \(\textbf{Vect}_{k}\): vector spaces over \(k\), 以及对应的线性映射;
  5. top: 拓扑空间以及对应的 continuous maps (连续映射).

Definition 1.1.4: 对于在范畴 \(\mathcal{A}\) 中的映射 \(f: A → B\), 若 存在 在 \(\mathcal{A}\) 中的映射 \(g: B → A\), 使得 \(g f = 1_{A}, f g = 1_{B}\), 则称其为 isomorphism (同构), 称 \(g\) 为 \(f\) 的逆.

吐槽

哦, 怪不得我觉得上线代的时候老师的用语非常的 “定语后置”, 现在自己读英文的时候, 感觉这种说法在简单直译的时候很正常啊…

Example 1.1.5: set 中的同构为 bijection.

Example 1.1.6: grp 中的同构及群同构, 类似的 ring 的同构为环同构.

Example 1.1.7: top 中的同构为同态.

(注: 因为不了解拓扑, 所以之后 top 的部分会尽可能跳过)

Example 1.1.8:

  1. 一个范畴可以直接说明其 objects, maps, composition 以及 identities:
    • \(∅\): 没有 objects 与 map;
    • \(\boldsymbol{1}\): 仅有一个 object 与单位映射 (其交换图就是一个点);
    • 一个包含两个元素和一个非单位映射的范畴 \(A \xrightarrow{f} B\);
    • 更多复杂的交换图:

      /_img/reading/basic-category-theory/examples-1-1-8-a.png

  2. 一些范畴可以除了单位映射外完全没有其他的映射, 称其为 discrete 范畴 (离散范畴);
  3. 当一个群只有一个元素, 并且所有的映射都是同构时即为一个范畴.
    解释
    • 考虑一个仅有一个元素 \(A\) 的范畴 \(\mathcal{A}\), 其有一个满足结合率的组合函数 (associative composition function):

      \[ˆ: \mathcal{A}(A, A) × \mathcal{A}(A, A) → \mathcal{A}(A, A)\]

      以及一个单位映射 \(1_{A} ∈ \mathcal{A}(A, A)\)

    • 于是有如下和群的对应关系:
      范畴群
      单元素 \(A\) 的范畴 \(\mathcal{A}\)\(G\)
      \(\mathcal{A}\) 中的映射\(G\) 中的元素
      \(ˆ ∈ \mathcal{A}\)\(G\) 中的 \(⋅\) 算子
      \(1_A\)\(1 ∈ G\)
  4. monoid: a set equipped with an associative binary operation and two-sided unit element.
  5. preorder: a reflexive transitive binary relation.

Construction 1.1.9: 每个范畴 \(\mathcal{A}\) 都有一个对应的 opposite (或 dual) 范畴 \(\mathcal{A}^{\mathrm{op}}\), 其定义为反转 \(\mathcal{A}\) 中的箭头方向.

  • 形式的定义:
  • 例子: 若 \(A \xrightarrow{f} B \xrightarrow{g} C\) 为 \(\mathcal{A}^{\mathrm{op}}\) 中的映射, 则 \(\mathcal{A}\) 的映射为 \(A \xleftarrow{f} B \xleftarrow{g} C\)/

Remark 1.1.10: 所有的范畴的定义, 定理以及证明都有一个反转箭头方向的 dual 形式.

Construction 1.1.11: 范畴的积 (product category) \(\mathcal{A} × \mathcal{B}\) 定义为:

\[\begin{matrix} \mathrm{ob}(\mathcal{A} × \mathcal{B}) & = & \mathrm{ob}(\mathcal{A}) × \mathrm{ob}(\mathcal{B}) \ (\mathcal{A} × \mathcal{B}) ((A, B), (A', B')) & = & \mathcal{A}(A, A') × \mathcal{B}(B, B') \end{matrix}\]

其中 \(\mathcal{A} × \mathcal{B}\) 中的映射 \((A, B) → (A', B')\) 是一个 pair.

不知道对不对的注记

感觉很像线性空间的直积.

简单的一个小节:

  • 这节大概定义了一个 “范畴” 是什么东西;
  • 范畴包含元素 (object) 的集合 (collection); 元素之间的映射 (map) 关系 (这些映射关系是如何组合 (compose) 在一起的, 单位映射);
  • 可以用交换图来表示一个范畴, 而将交换图中的箭头反向即可得到一个范畴的 dual.

Functors

Definition 1.2.1: 定义一个 functor \(F: \mathcal{A} → \mathcal{B}\) 由以下组成:

  • 一个函数:

    \[ \mathrm{ob}(\mathcal{A}) → \mathrm{ob}(\mathcal{B}) \]

    记作 \(A \mapsto F(A)\);

  • 对于所有 \(A, A' ∈ \mathcal{A}\), 其中的映射如下:

    \[ \mathcal{A}(A, A') → \mathcal{B}(F(A), F(A')) \]

    记作 \(f \mapsto F(f)\).

注: 相当于就是一个 functor 同时定义了范畴中元素 (object) 和映射 (map) 的映射关系.

满足一下的公理:

  • \(F(f' ˆ f) = F(f') ˆ F(f)\), 对于 \(\mathcal{A}\) 中的 \(A \xrightarrow{f} A' \xrightarrow{f'} A”\);
  • \(F(1_{A}) = 1_{F(A)}, A ∈ \mathcal{A}\).

Remarks 1.2.2: 1.

Appendix: English Dictionary

看到同学有读论文学英文的操作, 不妨也来试试:

  • multiplicative \(←\) multiplication \(←\) multiply
  • multiplicative identity 乘法单位元
  • homomorphisms (\(←\) Greek homoios morphe, “similar form”) 同态
  • isomorphism \(←\) Greek isos (equal), morphe (form, shape) 同构

    可逆的线性变换称为同构

  • inclusion \(←\) include
  • axiom: 公理
  • vague: 模糊的
  • bijection: bijective function, one-to-one correspondence, 一一映射
  • associative: 结合的 associate, association
  • dual