Simulate Physics
计算机模拟物理 - 农民的思路集和可能的学习路线
背景介绍
俺是个没文(头)化(脑)的人, 学习的时候没有一个非常直观的东西的话就总感觉理解起来非常心虚. 所以可能的话, 总希望能够有些什么清晰的东西东西来帮助我理解这些物理公式所代表的意义.
恰好同学问我了一些问题, 也激起了我的好奇心, 加上学长们的指导帮助, 接下去估计可以往这个方向来干一波鸟事.
(先介绍一些我之前试过的一些农民方法, 然后介绍一些可能的方向, 以后慢慢学. )
静电场和MMA
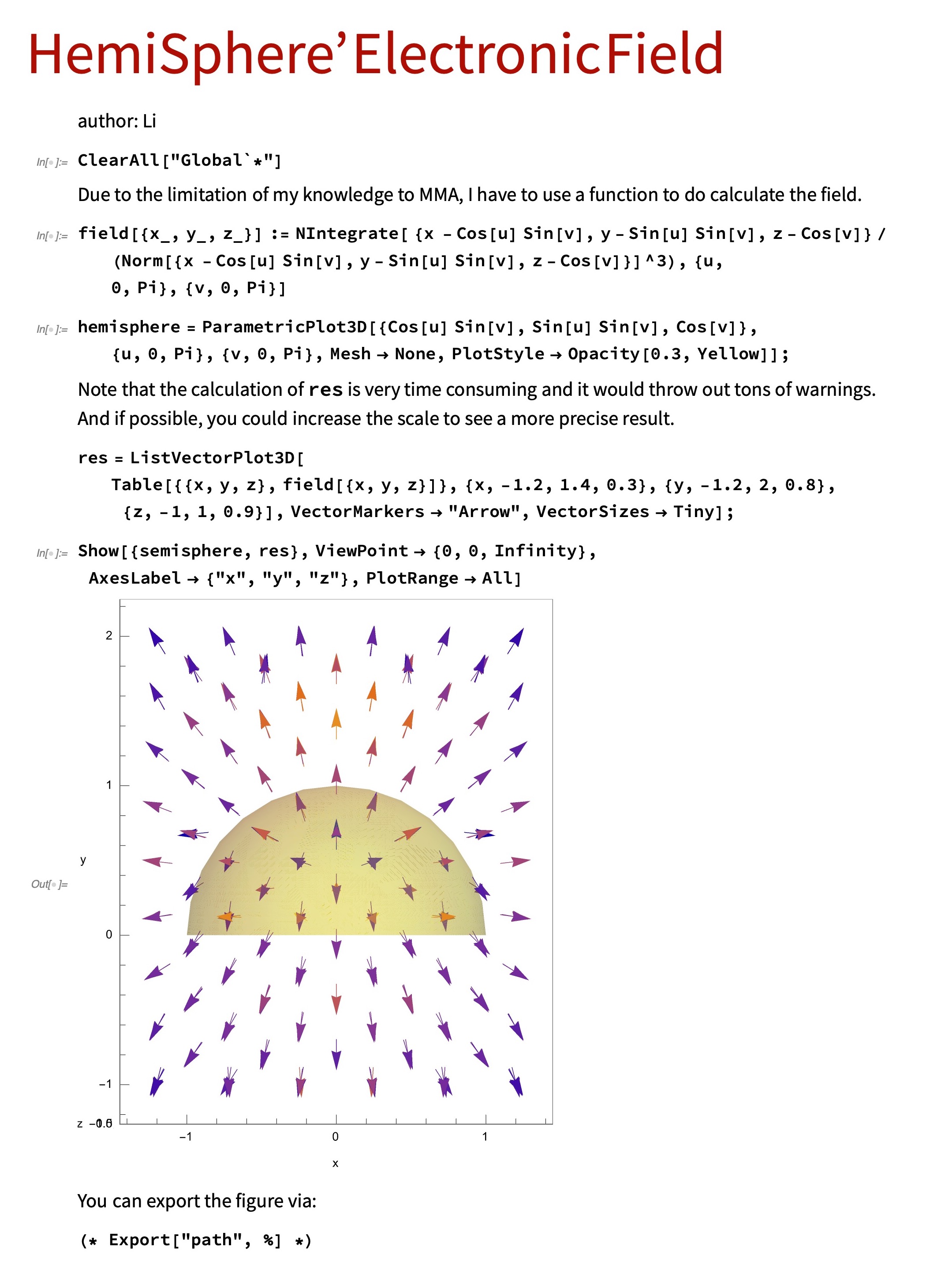
问题: 万磁王的瓜皮帽均匀带上电的话, 那么会有怎么样的电场. 即如何模拟一个均匀带点半球周围的静电场分布?
一个朴素的想法就是:
\[\vec{E} = \frac{1}{4 \pi \varepsilon_0} \frac{1}{r^3} \vec{r}\]积分就积分. 也不是不行. Mathematica里面的积分简单得很: Integrate[exp, {x, x0, x1}], 那么要如何直观地表现出来呢? 在Mathematica里面, 通过VectorPlot3D的方式可以在空间中画出向量场.
大意了. 提前说一下, 在Mathematica里面, 终止程序运行的快捷键是command-., 在Mac里面强制退出程序的的方式是鼠标右键-“Force Quit”, 实在没救了的话, 可以使用重启大法. (好的, 大概这就是我为什么会说大意了的理由了. )
那么能不能稍微变一下?
还是一个简单的想法: 在没有电荷分布的空间中, 电势满足
\[\nabla^2 \varphi = 0\]而由电场唯一性定理, 只要把电场的边界条件处理好就可以计算出全空间的电势分布了. (不过这个我没有实现, 因为啊, 偏微分方程不是很理解. 以后可以试试看. )
至少能动的水平
为了能够让程序至少给出一个令人满意的结果, 我尝试的思路就是将空间分隔为一个个的格点, 不再是计算连续的电场空间分布, 而是是离散地计算, 嗯. 没准能行:
(嗯, 能动了, 至少有了一个输出结果, 可是这样总感觉有点, 怎么说吧, 有点不够酷. 不过这个例子我觉得有些单调了. )
力学模拟和随便编程
前面的问题其实说是物理学模拟, 其实我觉得更像是一种我把物理公式交给计算机来帮我算的这样的想法. 那么下面来介绍一下让我更加想要了解用计算机模拟物理的一个例子吧.
问题: 我们考试选择题是A, B, C三选一, 所以我想要一个三面概率的骰子 – 一个圆柱形的骰子. 那么要怎么设计它呢?
(我的同学竟然打算用这个写小论文, 啊啊啊, 为什么不找一些更有意思的好玩的东西呢? )
不过这个小论文最核心的部分是如何通过理论验证来证明… 在上面的”小作文”里面, 模拟的数据是通过pybullet来模拟运算的. 怎么说呢? 不太懂. (以后可以多看看. )
于是打算用MMA来尝试一下, 结果模拟写到一半然后运行卡死了, 死了, 死… 完蛋. 心态炸了. 于是就换回了自己比较熟的Ruby. (关于Ruby的一些介绍, 啊, 啊, 呃, 好像我没有写过哦. 要不看看这个? 或者这个? )
最简单的想法
首先肯定不可能写运动方程的. 要能写出运动方程的话, 那还要模拟个啥啊, 哈哈哈.
马上开始: 如果物体的坐标超过了边界(比如地面), 那么就将速度反向. 这就是最简单的碰撞的想法. 嗯, 再乘上一个恢复系数就更好了. 大概长这样呢?
class Partical
def update
@x += @v * @dt
@v = @x > BOUNDARY ? - @e * @v : @v + force(@x) * @dt
end
end
(总觉得言语难以说清, 也没有一个很好的方式来表现. 之后会想一个方法来演示的. )
但是我要扔的是圆柱啊, 上面不是只模拟了一个粒子吗? 这差得很多的吧? 对于一个圆柱, 这应该是个刚体问题吧?
于是装模作样地写出碰撞方程, 然后解出关系, 最后就完事啦. 欧吼!
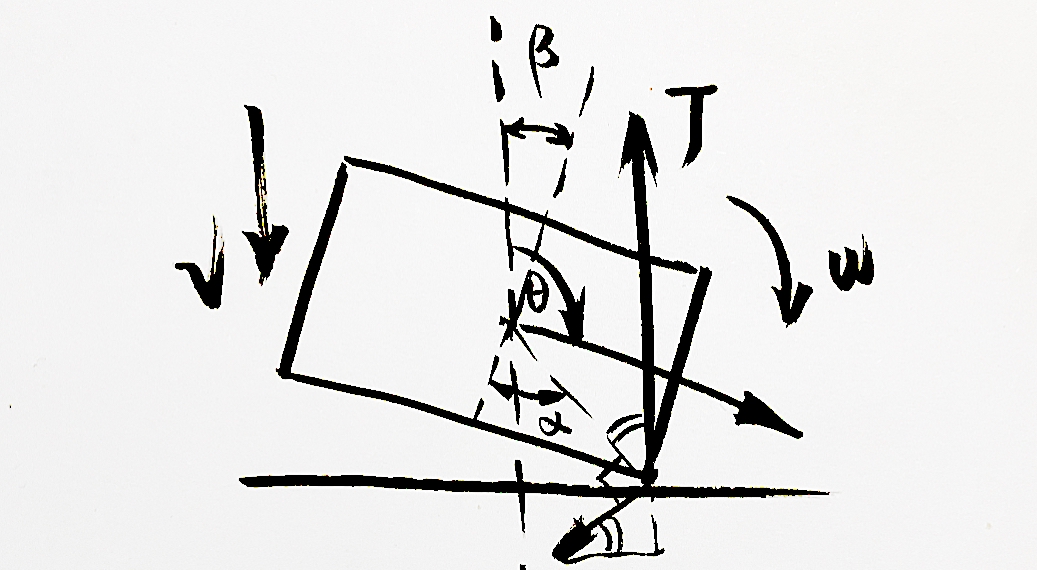
于是就可以计算出:

于是代码就变成了...
因为这个方法最终被我抛弃了, (做到一半出现了尴尬的结果, 所以我就放弃了, 话说这段代码还是我从Trash里面找出来的尸体呢. )def update
if @p + @r * Math.cos(@alpha - @theta) > 600 ||
@p - @r * Math.cos(@alpha - @theta) > 600 ||
@p + @r * Math.cos(@alpha + @theta) > 600 ||
@p - @r * Math.cos(@alpha + @theta) > 600
@p -= @v + 1
@theta -= @w
tringle = Math.sin(@alpha + @theta - Math::PI / 2)
deminator = @i - @m * (@r * tringle) ** 2
@v, @w =
-(@e * @i * @v +
(@e - 1) * @i * @r * @w * tringle +
@m * @v * (tringle * @r) ** 2) / deminator,
(@i * @w -
(@e + 1) * @m * @r * @v * tringle -
@e * @m * @w * (@r * tringle) ** 2) / deminator
# puts @v, @w
else
@p += @v
@v += G
@theta += @w
end
end那么实际上呢? 故事并没有这么简单, 问题出在一个很坑爹的地方, 即在模拟的时候, 在@dt和@v的配合得足够好的情况下, 会出现下面这样的尴尬情况: 在@x为BOUNDARY - 1, @v为10, @e为0.5的时候, 就会发生虽然反向了, 但是却因为恢复系数导致其并不能离开边界, 最终的结果就是卡碟或者瞬移之类的尴尬问题… (啊哈哈)
并且还有一个问题是因为表达式输入太复杂了, 一开始输入错了, 于是就尴尬, 超级尴尬的说.
问题总比办法多办法总比问题多
那么有没有一种方法, 可以简单而又美丽地解决这个问题呢? 有! 那就是使用能量的观点, 通过广义坐标和广义力的方式来处理问题.
那么首当其冲的, 就需要对能量进行偏导数. 一个比较简单的数值上的近似方式就是$f’(x) = (f(x + \delta x) - f(x)) / \delta x$. (而一个比较高级的方法就是通过一定的规则来进行符号处理, 关于这个, 在SICP里面有介绍, 这也是我最开始了解到符号计算的魅力的书, 之前读的时候也确实依葫芦画瓢实现了一个简单的. )
那么采用最朴素的数值近似方法, 就能够这样构造一个粒子对他粒子的作用: (以Lennard-Jones势为例. )
class Particle
atter_reader :x, :y, :vx, :vy, :energy
def initialize(x, y, vx, vy, energy = -> (x, y) {
# 加入一个对距离的考虑, 以防实在太近导致的DividedByZero错误
if (x - @x < 2 * DELTA || x - @x > 2 * DELTA) &&
(y - @y < 2 * DELTA || y - @y > 2 * DELTA)
0
else
r = 1000 * @size / Math.sqrt((x - @x)**2 + (y - @y)**2);
r ** 12 - r ** 6 # Lennard-Jones potential
end})
@energy = energy
end
def accelerate(obj, dx = 0.000_000_000_1)
-(obj.energy[@x + dx, @y] - obj.energy[@x + dx, @y]) / (dx * @m)
end
end
顺带一提, 这样的做法对于边界的处理也非常的方便, 只要将边界做一个近似, 看作是弹性的边界就能够处理碰撞问题了. (虽然在我写这个模拟圆柱的程序的时候还并没有考虑这件事情, 不过在之后我会介绍的. 这种巧妙的方式)
附上代码, 虽然可以下载的说. 虽然也估计没人想看的吧?
(观前提示: 因为这个代码没有重构, 所以里面写得非常的乱七八糟, 不过我也懒得改了就是. 原因看下面的失败分析. )require "gosu"
G = 0.05
E = 0.000_000_000_1
INI_POS = 300
INI_PHI = 0
INI_D = 50
INI_H = 90
MASS = 1000
BOARDER = 450
K = 0.01
class Cylinder
def initialize(x = 300, phi = INI_PHI, d = INI_D, h = INI_H, m = MASS)
@x = x
@pos, @phi = INI_POS, phi
@d, @h, @m, @i = d, h, m, m * (3 * d ** 2 + 4 * h ** 2) / 24
@r, @alpha = Math.sqrt(@h ** 2 + @d ** 2) / 2, Math.atan(@h / @d)
@v, @w = 0, 0
end
def energy(pos, phi)
dy1, dy2 =
@r * Math.cos(@alpha + phi),
@r * Math.cos(@alpha - phi)
e = 0
[pos + dy1, pos - dy1, pos + dy2, pos - dy2].each do |y|
e += y > BOARDER ? (Math.exp(y - BOARDER) - E * y * G * @m / 4) : - y * G * @m / 4
end
return e
end
def update
@pos += @v
@phi += @w
d = 0.000_000_000_000_1
@v += -(energy(@pos + d, @phi) - energy(@pos, @phi)) / (d * @m) - K * @v
@w += -(energy(@pos, @phi + d) - energy(@pos, @phi)) / (d * @i) - K * @w
end
def color(id)
[Gosu::Color::RED, Gosu::Color::YELLOW][id]
end
def draw
dx1, dx2, dy1, dy2 =
@r * Math.sin(@alpha + @phi),
@r * Math.sin(@alpha - @phi),
@r * Math.cos(@alpha + @phi),
@r * Math.cos(@alpha - @phi)
return @x + dx1, @pos - dy1, color(1),
@x + dx2, @pos + dy2, color(1),
@x - dx1, @pos + dy1, color(0),
@x - dx2, @pos - dy2, color(0)
end
end
class Simulator < Gosu::Window
def initialize
super 600, 800
@cylinders = [
Cylinder.new(300, rand * (Math::PI / 2))
]
end
def button_down(id)
@cylinders << Cylinder.new(self.mouse_x, rand * (Math::PI / 2)) if id == Gosu::MS_LEFT
end
def update
@cylinders.map { |cylinder| cylinder.update }
end
def draw
@cylinders.map { |cylinder| draw_quad(*(cylinder.draw)) }
end
end
Simulator.new.show不过这里要指出一点, 在我写完代码之后, 过了一个晚上, 睡前看番的时候, 突然想到了一个致命的问题: 那就是里面的转动项搞错了. 也就是说, 虽然最终看起来还真挺像那么回事, 但是并不是十分物理.
为什么错了的答案揭晓.
如果仔细看代码的话, 就会发现我计算能量的方式是通过边角的四个点来做的, 这样的思路是从之前的通过四个点来检验碰撞的想法继承过来的. 虽然这样做并没有任何的错误, 但是这就是问题的来源, 即因为只有四个点, 所以我的模拟会更像是一个立方体的转动表现而非一个圆柱体的转动表现. 这就是我的失败的地方. 也就是说, 为了弥补这样的错误, 我需要将这个问题变换为对一组点的能量计算.
因为意识到了上面的错误, 所以我开始了新的想法: 那就是对一堆粒子的处理, 然后对于刚体的话, 就看作是粒子的集合就好了.
一堆粒子和统计的模拟
问题: 其实这个问题挺无聊的, 有点像是为了考试特地去出的那种垃圾问题. 真的挺无聊的, 如何模拟一堆粒子限制在重力场中的运动. (其实就是为了写一个能够实现我上面的粒子集合的目标的通用的库的尝试. )
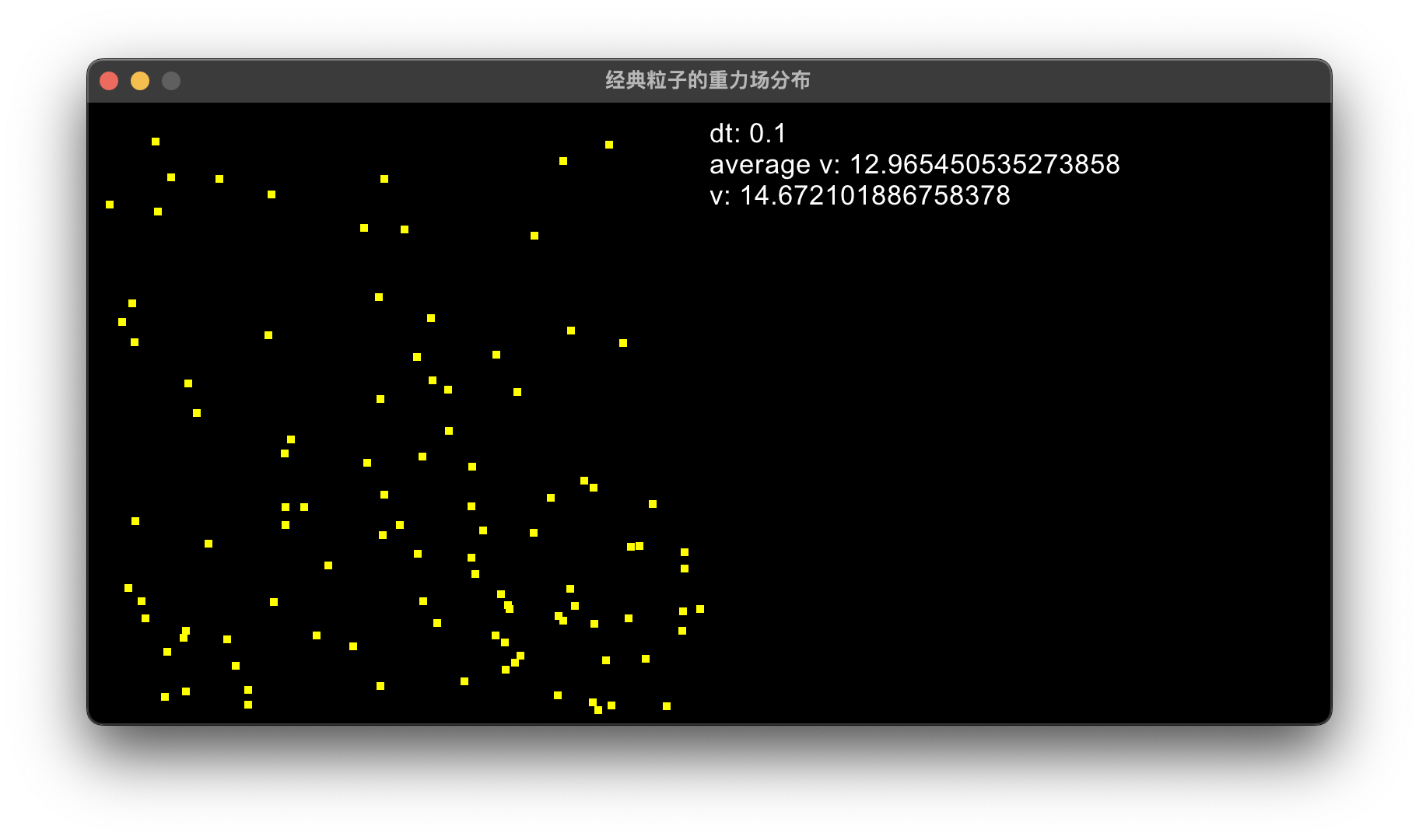
总而言之, 就是对上面的问题解决思路写一个更加规范的框架, 然后将它们应用起来不就完事了? so easy. 嗯, 一开始我确实是这么想的.
但是很快, 愚蠢的计算机就给了我大大的耳光子: 一些在边界上本该被弹回来的粒子, 因为运动速度太快, 一下子过于深入边界, 结果收到了过于强大的弹力, 竟然以更快的速度弹回去了! 这样的事情绝对很奇怪啊!
所以我的面前产生了这样的一个问题, 如何让一个物体运动得很快但是又不是很快呢? 而我交上去的答卷就是: 芝诺时. 一开始我是依赖计算机(gosu库中的update的刷新fps来控制模拟的时间的, 用人话说就是在每次模拟的循环中@dt是相等的. ) 但是为什么不换一个思路, 设置一个@dx的模拟位移上限, 来保证不会出现因为速度太快而产生的误差呢? (说得花里胡哨一点就是, 将时间)
于是我加入了类似于这样的操作:
if @v * @dt > @max_dx
@dt = @max_dx / @v
@x += @max_dx
else
@x += @v * @dt
end
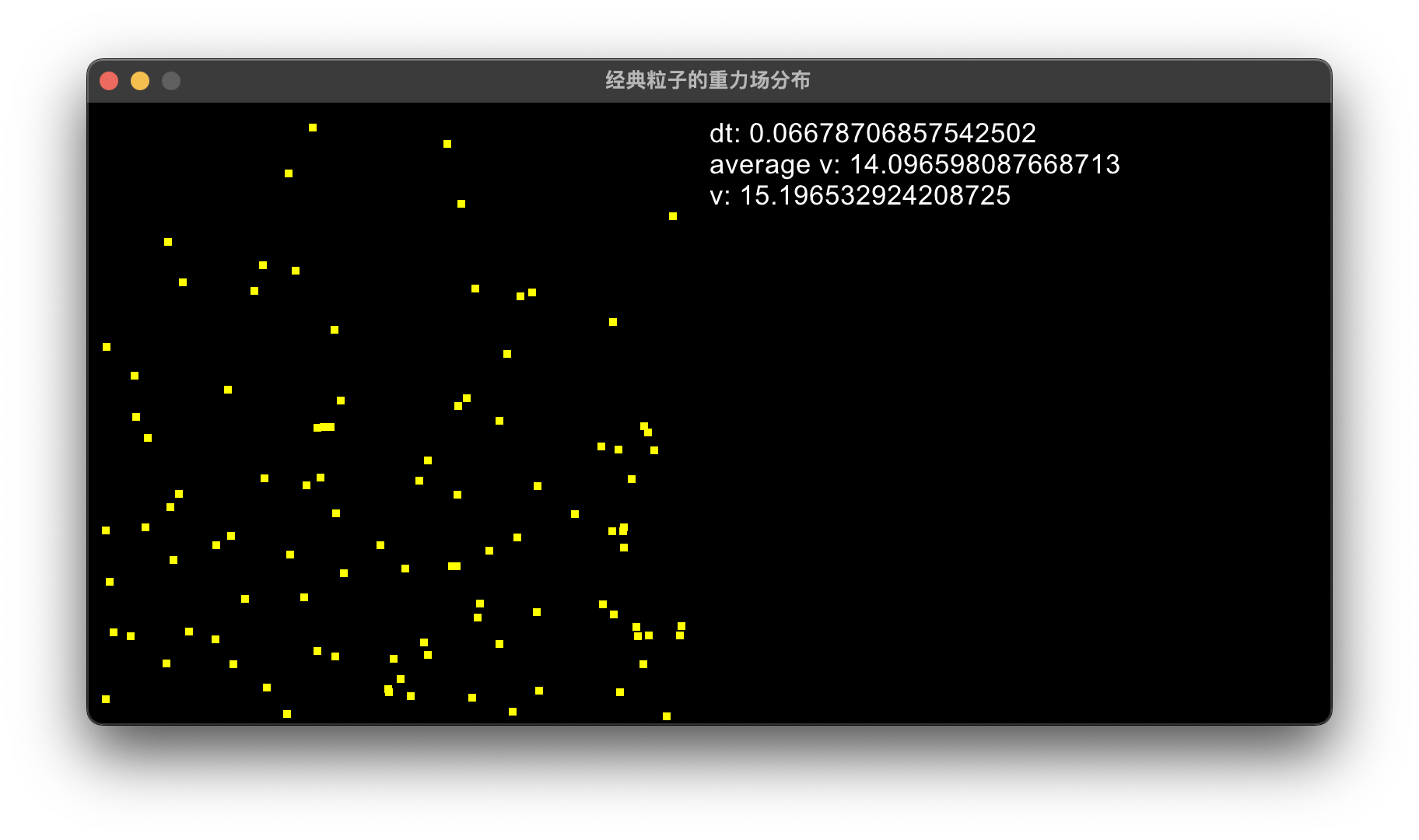
于是最终的效果类似于这样:
(又是自爆时刻: 这个程序运行得很慢, 在200个粒子的模拟的时候就出现了问题, 所以一个想法就是如何将程序优化, 另一个想法就是如何多线程计算. 虽然感觉这个不应该由一个臭搞物理的人来操心, 总该是有什么计算机的或者数学的牛人想过的事情. )
那么接下去该干什么?
对自己的程序的想法
事不宜过三, 目前我想要:
- 把程序写得更加通用一些. 毕竟现在里面的所有参数都是我瞎掰的, 如果参数调的不是那么合理的话, 模拟起来就会出bug, 这样一点也不酷. 所以我打算把程序的接口做得精巧一些, 最好能够像这样定义一个物体:
gravity = Field.new particle = Particle.new( x: rand(100), y: rand(100), z: 0, vx: 0, vy: 0, vz: 5, mass: 10, mass_unit: :g )并且我也想要把这样的功能融合进我在学的计算机代数里面. 嗯, 先画一个饼. 至于能不能实现, 就走一步算一步.
- 刚体或者说是粒子集合体. 虽然感觉这个应该比较好实现, 但是具体实现的时候可能还是有点困难. 嘛, 慢慢来.
- 更加的直观简单的模拟. 毕竟怎么说吧, 写代码对人来说并不是很友好, 也看起来不像是在做实验. 如果能够将物理模拟变成一个像是真正做实验一样的事情就好了.
(感觉这三个愿望好像许得有点大了… 我靠, 真的诶. 又不是奇趣蛋. )
确实有点闭门造车了
上面的做法感觉十分的不妙啊, 因为感觉实现的方法太过朴素了. 不能体现数理专科学校的特长. 并且实现的方式太过特殊. 所以我需要学习!
于是在好心的学长的介绍下, 接下去就应该要多了解一些关于计算机模拟的事情, 并且还要多看别人的代码. 了解前人是怎么想的.
废话集
其实不光是物理, 感觉数学里面的东西实现了一遍之后总感觉有一种, 啊, 我比原来多懂了一些的感觉. 然后就能够理解为什么需要像这样形式化地定义, 这样形式化的定义有什么好处的一些感觉. (比如还在搞的计算机代数, 虽然现在理解得并不是太多. )
比如很早之前在一本书上读到理论力学容易失去直观的物理图像之类的话, 一开始在我只是看书上那些”漂亮”公式的时候, 我确实觉得它们真是一点也不直观. 但是后来慢慢觉得, 这些不就是换了一种形式的$F = m a$吗. (不过可能并不是只有这样的意义, 以后还要慢慢理解… )
哦, 不过好像费曼说过这样的一句话: 假如你要用计算机模拟物理的话, 最好是量子的. (力学课上的依稀印象, 为了证实这段话, 我去网上搜索了一下, 结果, 发现了一篇很厉害的演讲/论文. 那么接下去一段时间就先看看这篇论文吧. 不过这里好像有一个费曼关于计算物理的论文合集? 不清楚, 总之之后会把阅读笔记给写出来的. )
最后.
计算机真的是蠢蛋!