Dot, Dot, Dot and …
点, 点, 点, …
点
大约是在今年一月中旬, 我抬起头来, 第一次看见了墙上的那个斑点. 为了要确定是在哪一天, 就得回忆当时我看见了些什么. 现在我记起了炉子里的火, 一片黄色的火光一动不动地照射在我的书页上; 壁炉上圆形玻璃缸里插着三朵菊花. 对啦, 一定是冬天, 我们刚喝完茶, 因为我记得当时我正在吸烟, 我抬起头来, 第一次看见了墙上那个斑点…
《墙上的斑点》 弗吉尼亚·伍尔芙
这是一个点:

通常在某些学科中(比如数学和物理里), 点没有大小. 所以下面的也算是一种点:

但是, 是不是稍微有点过分了呢… 右边的点的画纹是多么的漂亮和美观, 它的形状和朝向又是这样的优雅和… (咳, 吹不下去了. ) 但是如果你把镜头移开一点点, 让画面变得更大一些, 于是之前(右边)的点也没有那么得”庞大”了.

于是我们不妨思考一下, 到底怎么样才算是一种点? 这个时候不妨我们带上”战术目镜”, 把所见的一切东西的”战斗力数值”都显示在一个表格里面:
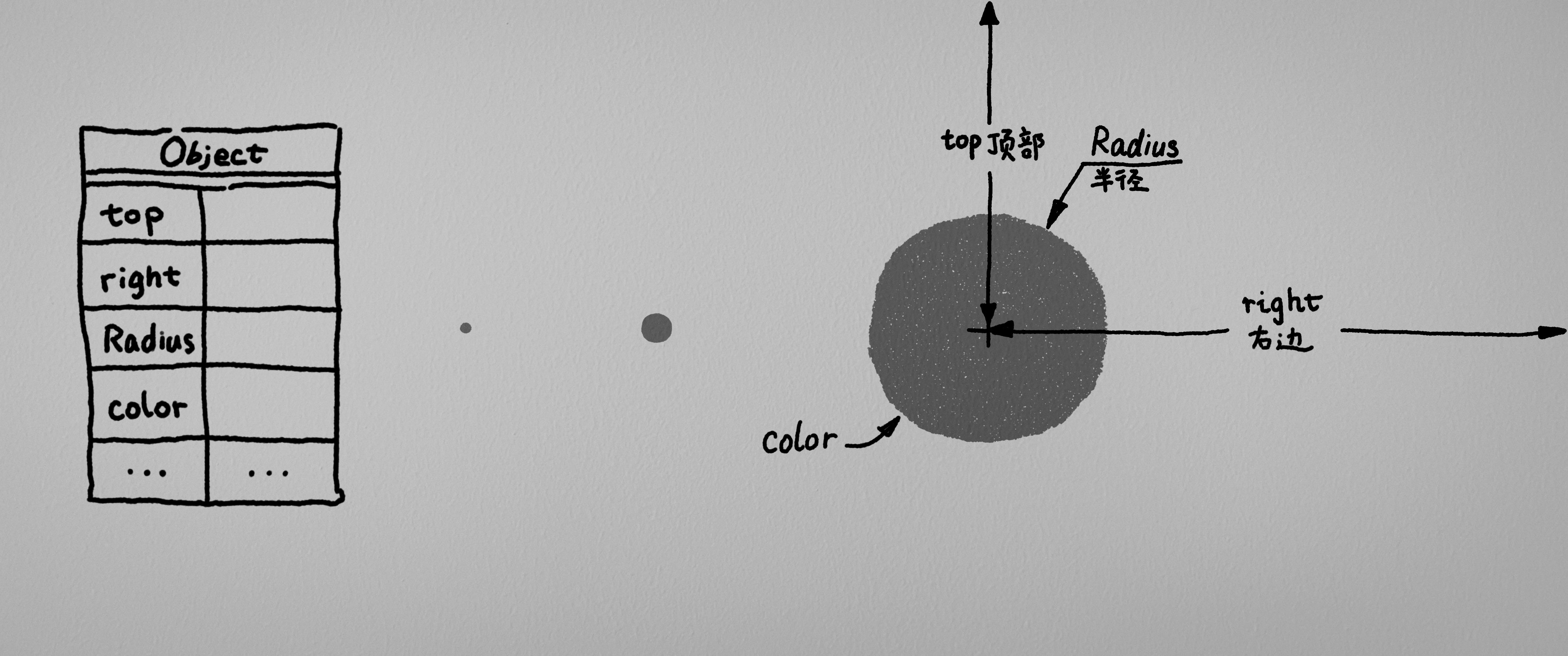
假如对任何一个物体, 我们都能够想一个方法把它的信息全部写进一个表格里面. 那么在某种程度上来说, 我们便可以将物体用表格来等效地表达和代替.
但是现实世界中, 要描述一个物体可能需要非常多的信息, 即一个物体对应了一个非常多行的表格. 处理众多的信息是非常麻烦的一件事情, 所以一个简单的思路就是: 只关注一部分的信息.
假如我们只保留物体的位置(也就是top和left的信息, 或者专业一点, 叫做”坐标”. )信息, 那么不论物体的其他特征再怎么花里胡哨, 在我们的眼中, 也不过就是一个简化的坐标 – 或者说, 一个抽象的”点”.
但有时候, 我们也可以不那么”激进”, 可以多保留一些信息, 比如质量(比如一个5公斤的点), 速度(比如一个$5cm/s$的竖直下落的点), 角动量(想象一个旋转的点着实有些困难)等等. 于是我们就得到了五彩斑斓的点:

在这样的理想化抽象中, 现实中的复杂对象便被”投影”到了特定的表格中. 于是需要处理的信息的数量便减少了, 处理的难度也相应减少了. (这就是妙哉妙哉摸鱼法bushi)
假如你想要一些别的观点
干脆也能够说, 这样的投影就像是将在信息空间中的代表物体的信息的向量投影到位置空间和其他的空间的直和的新的空间.
那么稍微详细一些介绍就是:
如果我们用一个"向量空间"来表达物体的信息, 比如最常见的"用一个位置矢量$\vec{r} = (x, y, z)$来表达位置信息", 又或者是稍微不那么"常见"的色彩空间"用RGB(0~255, 0~255, 0~255)的一种'坐标'来表示色彩信息"等等. (尽管对于某些信息, 我们并不能像这样直接进行加减运算, 比如被费曼嘲讽的"天空中有一颗一等星, 两颗二等星, 求总的星等级"的离谱问题. 所以并不能严格地说是一种"向量空间". 但是因为我们是为了方便在后续使用数学工具来处理问题, 所以对于这些问题, 还是先放一放吧. 假如读者有什么好方法来解释的话... )
处于上面的"向量空间"的物体可能会有近乎无穷多的信息(维数近乎无穷). (并且这些信息也并不一定是相互无关联的, 比如一个动量为$5 kg \cdot m / s$的信息, 可能和质量为$5kg$, 速度为$1m/s$这两条信息是重复的, 即信息之间存在一定的冗余. )所以为了简化研究, 我们可能只能够了解到一定的信息; 又或者是出于研究手段的局限性, 我们仅仅能够观测到物体的一部分的信息. (比如我们可能只能通过照相机来拍照观察物体, 只能了解物体在照像平面上投影的信息. )
对于前者, 出于简化研究的目的, 我们将代表物体的"向量"经过投影算子$\mathcal{P}_{V_{from}\rightarrow V_{to}}$, 只留下特定的信息. 这样的做法有利于让问题更加容易分析, 不仅仅是因为分析的东西少了(比如以物理中的自由度的概念为例, 假如我们将每一个点所带有的信息数量(信息的向量的维数)看作是一个自由度, 那么自由度越高, 为了确定这个物体就需要更多的约束方程或者"运动"方程. 处理起来就会更加麻烦一点. ), 更是因为减少了无关信息的干扰. (用人话来说, 就是在一间嘈杂的屋子里, 带上了耳塞安静地看书). 一个常见的例子就是在图像处理的时候, 通过灰度 -> 梯度 -> 来处理图像的边缘以便于后期的识别和处理. (一种可行的思路, 本人还没专业学过数字图像处理. )
而对于后者, 则是一种因为观测认识有限而导致的信息有限的问题. 这个时候, 我们就需要想办法来从这些"有限"的信息中还原出原本的物体. 比如说, 我们只知道一个物体会在一个平面区域内出现, 那么我们只能说在某一个平面子区域的出现概率为多少. 而如果知道的信息更多, 譬如其分布为以中心为原点的一个高斯分布, 又或者是一个粒子从原点出发进行二维无规律随机行走... 那么我们对粒子的分布的情况的了解程度(或者说, 分布的种类的所对应的概率)便会更加的清楚. (参见"星期二男孩"问题)
点, 点
线之界是点 <凡线有界, 两界必是点. >
《几何原本》 欧几里得(著), 玛利亚 徐光启(译)
如果我们目前只考虑物体的位置, 忽略其他的信息, 然后来看下面的图:

我们会发现, 虽然在上面的那件文物作品上的花纹仅仅只是最朴素的点(戳戳), 但是一个个的点组合在一起, 却能够形成有规律的图案: 三角形, 环带等等. 在某种程度上来说, 原本我们通过”点”的模型简化了的信息, 在点与点之间的关系中, 又重新被表现了出来. 那么我们为什么不反过来思考: 能否把一些复杂的图形, 对象, 物体来用一些简单的基本的”点”(我们前面应该很熟悉这个点的故事了吧. )来表示呢?
众所周知, 有色差的地方就能够有Bad Apple…
啊, 不是. 是两点确定一条直线(大概). 就像是《超能陆战队》中的大白的眼睛一样:

于是只要有两个点, 我们就能够知道同样在直线上的其他点的位置信息了. 这样的方式是多么的便利啊! 并且既然会画了直线, 那么距离画曲线还会远么? (古人云: “三岁小儿皆可握笔涂鸦, 以直代曲, 有大拙之美. “bushi)

于是, 想要用直线来表现曲线(比如上图中的头发”曲线”), 只需要在曲线上选择合适的特征点, 然后用直线连接特征点, 就能够在一定程度上表现曲线的神韵了. 也就是说, 我们通过用直线上的点来代表曲线上的点的方式来近似地表现曲线. 而倘若我们能够将特征点的数量增加到一定的程度, 然后眯上眼睛 – 看上去这样的直线就变得像是一条曲线一样了.
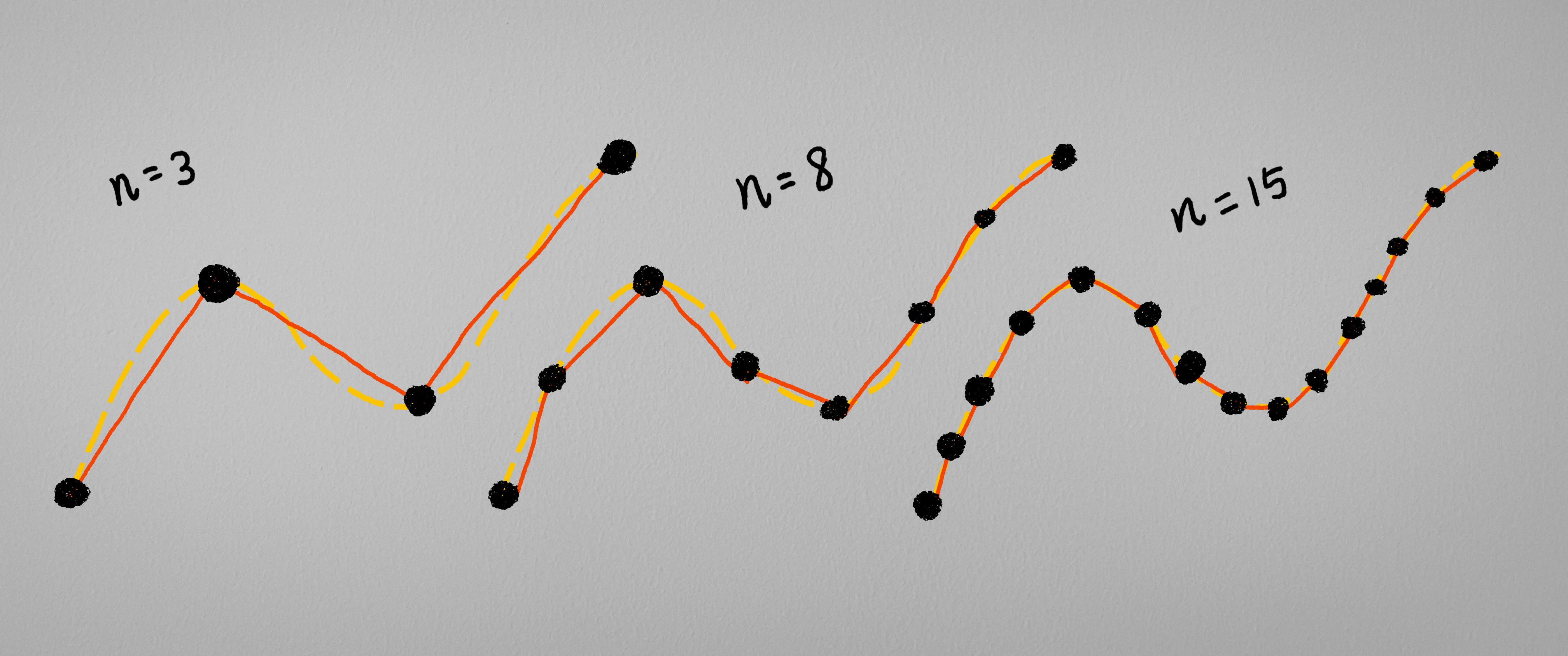
可以发现, 随着特征点的数量越来越多, 我们的直线段的集合越来越接近曲线.
也许有杠精会说, 那怎么可以呢? 我大工匠精神要的就是这手工艺的美妙曲线, 你的直线是工业化的机械的直线, 没有我工匠精神的灵魂! 我的手捏出来的曲线, 每根线的误差都不到$\varepsilon$的误差.
那么面对这样的杠精, 我们能做的只有 – 进一步地增加特征点的数量, 比如说当特征点数量$n \geq N(\varepsilon)$时, 我们的误差$\vert\Gamma^{直线}_n - \Gamma^{曲线}\vert$便会小于$\varepsilon$. 于是我们便可以自豪地邪魅一笑: 我的也能够逼近曲线. 用数学的语言来说便是:
\[\forall \varepsilon > 0, \exist N(\varepsilon), \forall n > N, \vert\Gamma^{直线}_n - \Gamma^{曲线}\vert < \varepsilon \Leftrightarrow \lim_{n\rightarrow\infty}\Gamma^{直线}_n = \Gamma^{曲线}\]同理, 我们也能够将这样的方式应用到曲面, 立体的问题上. (既然你已经学会了一加一了, 那么请…) 回忆前面”点”的处理方法, 我们会发现, 这样的选择特征点来代表物体的更加复杂的信息和原来的抽象近似是异曲同工的: 都是通过仅保留一部分的信息, 来达到对原始物体的状态的描述.
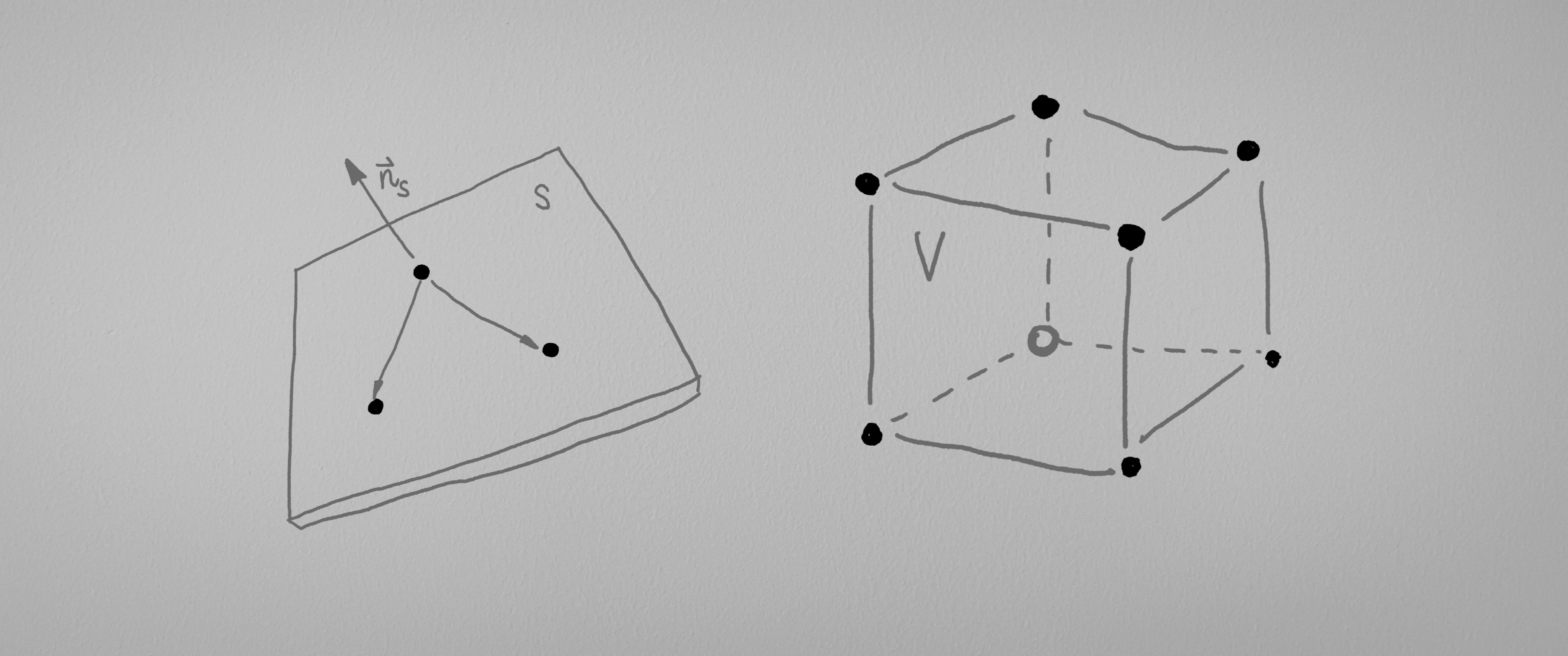
最后, 我们不妨以其中的平面为例... (没事, 假如你不想看的话, 我帮你折叠了, 点我展开)
(假如你看过了前面的折叠部分. 那么请自动忽略下一段. )
我们可以把平面用三个点来表现的这个问题看作是一种用少量的信息来还原物体的一种方法. 就像是:)用简单的符号就能还原出一张笑脸一样, 如何从少量的(或者是破碎的)信息中还原原本的信息, 是一个非常有意思的问题. 夏洛克·福尔摩斯先生用的是"演绎法": 观察, 归纳, 推理, 总结. 我们的方法也是类似的(不过用上了数学这个强大的工具).
众所周知, (欧几里得空间)对于一个平面, 存在一个向量(平面法向量)和平面上的所有向量都垂直. 而学过一点点矢量运算就能知道, 两个矢量的叉乘的结果和这两个矢量都垂直. 并且平面上的所有向量都可以用平面上的两个线性无关的向量的线性组合来表示.
那么我们既然知道了平面上的三个点: $\vec{r}_1, \vec{r}_2, \vec{r}_3$. 于是就能够得到平面上两个向量$\vec{r}_2 - \vec{r}_1, \vec{r}_3 - \vec{r}_1$, 于是和这两个向量垂直的$\vec{n} = (\vec{r}_2 - \vec{r}_1) \times (\vec{r}_3 - \vec{r}_1)$也同时和它们的线性组合垂直. 所以与平面上的任意向量都垂直, 即为平面的法向量.
于是平面上的所有的点都变成了$(\vec{r} - \vec{r}_1)\cdot\vec{n} = 0$的方程的解. 于是我们就还原了整个平面的位置信息. 这个时候, 我们就是靠着数学的这个工具来还原平面的性质. 多么巧妙啊.
点, 点, 点
If this is to be proved and the type of computer is as I’ve already explained, then it’s going to be necessary that everything that happens in a finite volume of space and time would have to be exactly analyzable with a finite number of logical operations.
Richard P. Feynman, Simulating Physics with Computers, May 7, 1981
(以下是本人渣翻译, 为了读者考虑, 上面是原文)
如果存在我(费曼)之前假设的那种通用计算机的话, 那么(利用计算机来模拟物理)就需要通过在有限的空间和时间中进行有限次的逻辑运算来实现.
理查德 P. 费曼, 用计算机模拟物理, 1981年5月7日
正如我们上面所说的那样, 为了简便运算和处理, 我们将物体抽象简化为点的模型来考虑. 而又为了更好地表现物体的其他信息, 通过加入更多的点(或者说是引入点与点之间的关系)来承载和表达物体更多的信息.
但是不要仅仅局限于如何把数据记录下来, 格局要打开, 为什么不问问神奇海螺呢?试试看让这些数据代替现实中的物体进行一个模拟运动呢? 比如说物理课上的$\dot{p} = m \ddot{x}$的公式就是一种用抽象的数据来代替现实中真实物体的方法.
在物理中的数学量(一般)都是一种(随着时间)连续变化的数学函数. 譬如在占据物理学大半江山的振子运动中$\ddot{x} + \omega^2 x = 0$, 对于一个解$x(t) = A \sin(\phi + \omega t)$中, 物理量$x(t)$便是一种随着时间连续变化的量. 在数学上, 不论多么精确的$x$的数值都是可能的 – 因为$\sin$是一个连续函数. 而在(一般的)物理图像中, 好像也应该是这么回事 – 因为空间是连续的. 如果把这些”连续”的函数画在图上的话, 那么看上去就会像是一条平滑的曲线. (注: 严格定义并不是”图像是平滑曲线的函数是连续函数”. )
但是为什么我们不借鉴一下前面的”点”的思想, 通过一定的”特征点”来描述这些物理量的变化关系呢? 于是本来连续的物理量就被分割成了离散的量. 而这样的东西便可以交给计算机来处理. 于是用计算机来模拟物理世界的问题开起来便十分具有吸引力了.
首先是时间, 假如我们考虑一个简单的匀速直线运动: $x(t) = v t$, 那么在时间轴上选择一些特征点进行分割, (就像是用一台相机定格住一瞬的空间), 沿着这些特征点分割出来的”空间”不妨让我们看作是一种”状态”, 根据特定的规则, 从这个时间点跳转到下一个时间点时, 我们的状态会发生改变. 用人话来说就是: 从$x(t_0)$的状态变化到了$x(t_0 + \Delta t) = x(t_0) + v \Delta t$的状态.

如果你想要用一些更加别致的眼光来看这个问题...
我们不妨把这样"状态转移"的问题看作是一种"拓展版的自动机"的问题:
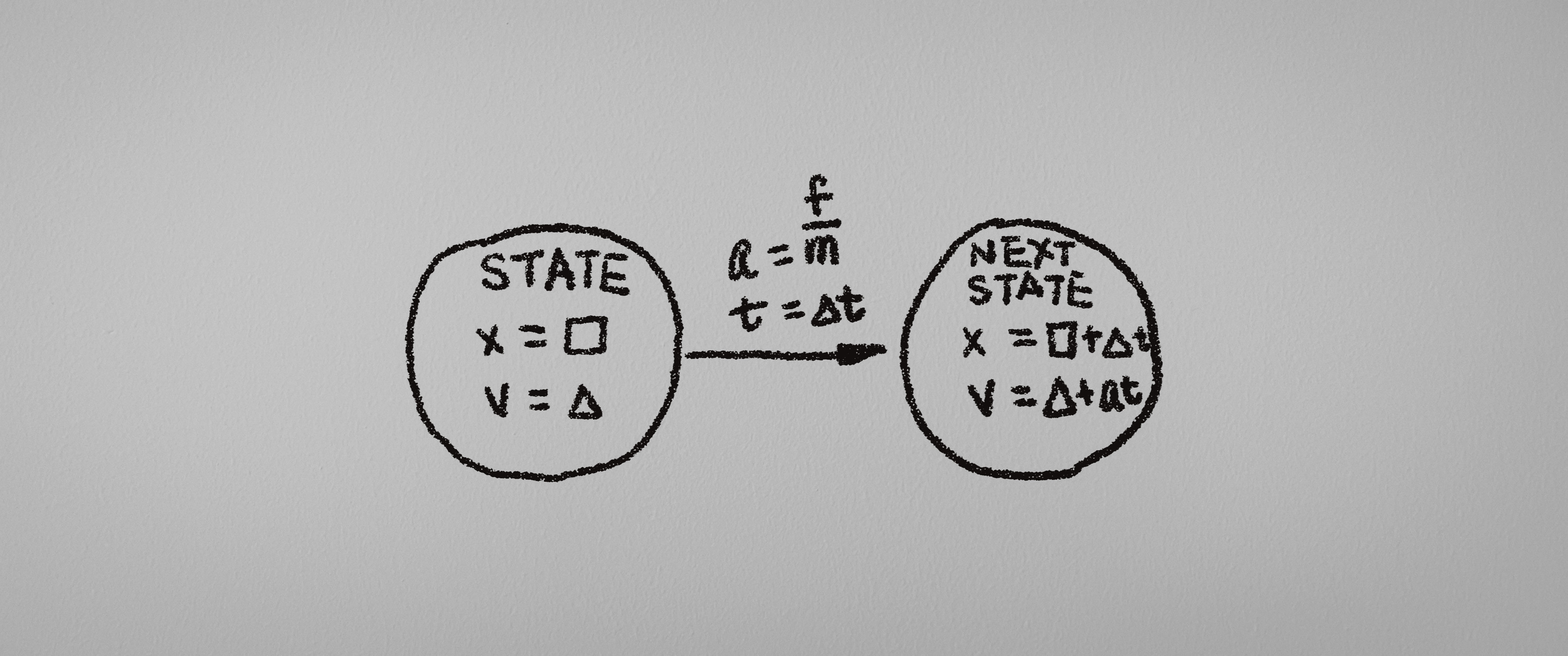
嗯, Talk is cheap, show me the code. (其实是一个非常水的代码)
# ruby
# 简单的对象类
class Thing
NO_FORCE = -> (x, v, t) { return 0 } # 不受力
# 初始位置x, 初始速度v, 模拟时间间隔dt
def initialize(x, v, dt)
@x, @v, @dt, @t = x, v, dt, 0
end
# 从当前状态转移到下一状态
def update(force = NO_FORCE)
@x, @v, @t = @x + @v * @dt, @v + force.call(@x, @v, @t) * @dt, @t + @dt
end
# 一个用来简单输出模拟结果的函数
def emulate(force = NO_FORCE)
loop do
update(force)
sleep @dt
puts @x
end
end
end
# run the emulation
a = Thing.new(0, 1, 0.01) # 从原点以速度1出发, 模拟的间隔时间为0.01
a.emulate # 0.01, 0.02, 0.03, 0.04, 0.05 ... ## 一个匀速运动...
b = Thing.new(2, 0, 0.01)
b.emulate(-> (x, v, t) {
-1 * x - 0.1 * v # 弹力和阻力...
})于是我们的计算机就能够开始一定程度地模拟物理上的一些行为了.
还记得前面对于精度的那个抬杠问题么? 同样的, 我们在模拟的时候也会遇到精度的问题, 如果我们遇到了运动波动非常大的运动, 那么就需要更多的特征点. 但是作为摸鱼大户, 看到一条几乎平直的线上打满了点, 而一条蛇形的曲线巧妙地”避开”了点…
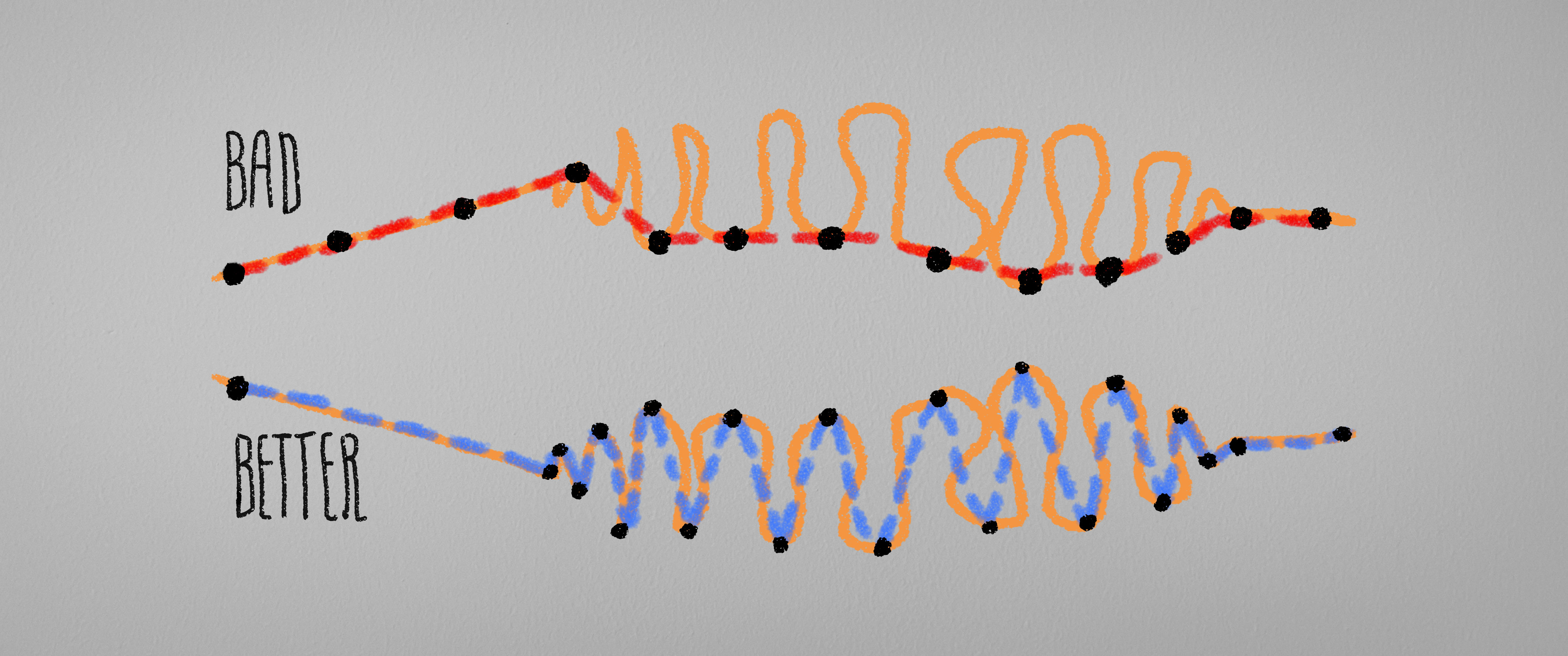
我们会发现, 与其单方面增加(均匀分布的)点的数量, 有时候不如换一个思路, 选择变化大的地方, 增加其特征点的数量, 来保证信息能够被更好地保留.
如果你想要看一些代码...
# ruby
class Thing
MAX_DISPLACEMENT = 0.1 # 限制变化上限
def update(force = NO_FORCE)
dt = @v * @dt > MAX_DISPLACEMENT ? MAX_DISPLACEMENT / @dv : @dt
@x, @v, @t = @x + @v * dt, @v + force.call(@x, @v, @t) * dt, @t + dt
end
end(注: 上面的代码并不是完美的代码解决方案. 一个稍微比较能动的例子就是我在Simulate Physics中写的那几个. 不过感觉并没有写得很好, 拓展性太差了. 并且效率也很低, 未来可能会修改. )
点, 点, 点…
那么最后来一个比较”实在”的例子(参考: Understanding the Finite Element Method (Youtube), 以及《理论力学》梁昆淼)做收尾吧: 如果我们想要了解一个弹性立方体在特定受力下的形状.
我们将一个立方体看作是具有质量的点的集合. 并且众所周知, 有弹性(非刚体)的物体在受到外力作用的时候会发生形变. 于是我们不妨在点的基础上再附加一个信息: 即形变的大小, 假设是一个三维欧几里得空间(或者三维空间中的直角坐标系)中的立方体, 那么其位移便可以用分量来表示: $\delta\vec{r} = (\delta x, \delta y, \delta z)$.
数学的说法
看作是一个映射: $f: \vec{r} \mapsto P(\vec{r})$. 即一个位置和点的映射.
而点可以看作是一个"向量", 或者说是位移的一个笛卡尔积. $\delta X \times \delta Y \times \delta Z$.
最简单的版本
众所周知, 有弹性的物体可以被压缩, 被压缩的物体会有一种返回原本状态的”趋势” – 即有一个反弹的力(即压缩后的弹性物体在一定程度上会产生一个近似和压缩量成正比的回复力). 用一个叫做”胡克定律”的公式写出来便是:
\[\vec{F} = - k \delta\vec{r}\]胡克定律
在梁先生的理论力学一书中, 这样定义: "弹性棒伸长或缩短时, 任一横截面两方的相互作用力$F$正比于棒的伸长或缩短$l$", 即$F = k l$.
据维基百科的说法, 在最早的发表(来源于对弹簧钟的制作)中: 胡克定律是一串打乱的拉丁字谜: "ceiiinosssttuv" (如果不能确认自己的发现, 就在发表时先把自己的发现打乱字母顺序后发表, 在确认后再公布结论. 嗯, 着实是一种方法. ), 真实的顺序则为: "ut tensio sic vis", 即"力如伸长(一般变化)". (其实这感觉就和我们古代的中国人的文献一样了, 说得很简单晦涩, 比如"道可道, 非常道"之类的, 而现代的科学则需要更加严格没有歧义的解释. 这么说来, 我们也算是踩在巨人的肩膀上的发展了. )
不过传说, 牛爵爷的这句"踩在巨人的肩膀上"却是在对胡克的一种嘲讽 -- 嘲讽胡克的矮小. 但是抛开胡克和牛顿等人的矛盾不谈, 胡克却是是一位非常有光彩的科学家. 在英文的维基百科中是这样描述胡克的: "polymath"(在中文中则是"博物学家"). 确实, 作为早期的有名的科学家之一, 胡克的研究涉猎非常的广泛, 并且对多种科学分支都有基础性的一些贡献.
(嘛, 某种程度上来说, 生得早一些也有一点点的好处. )
而将同一物体的不同部分相互连接在一起, 于是就能够得到一连串的受力和位移的关系, 将这些关系组合在一起, 那么我们便能够知道物体中的力的分布. 举个例子(超级简单的例子):
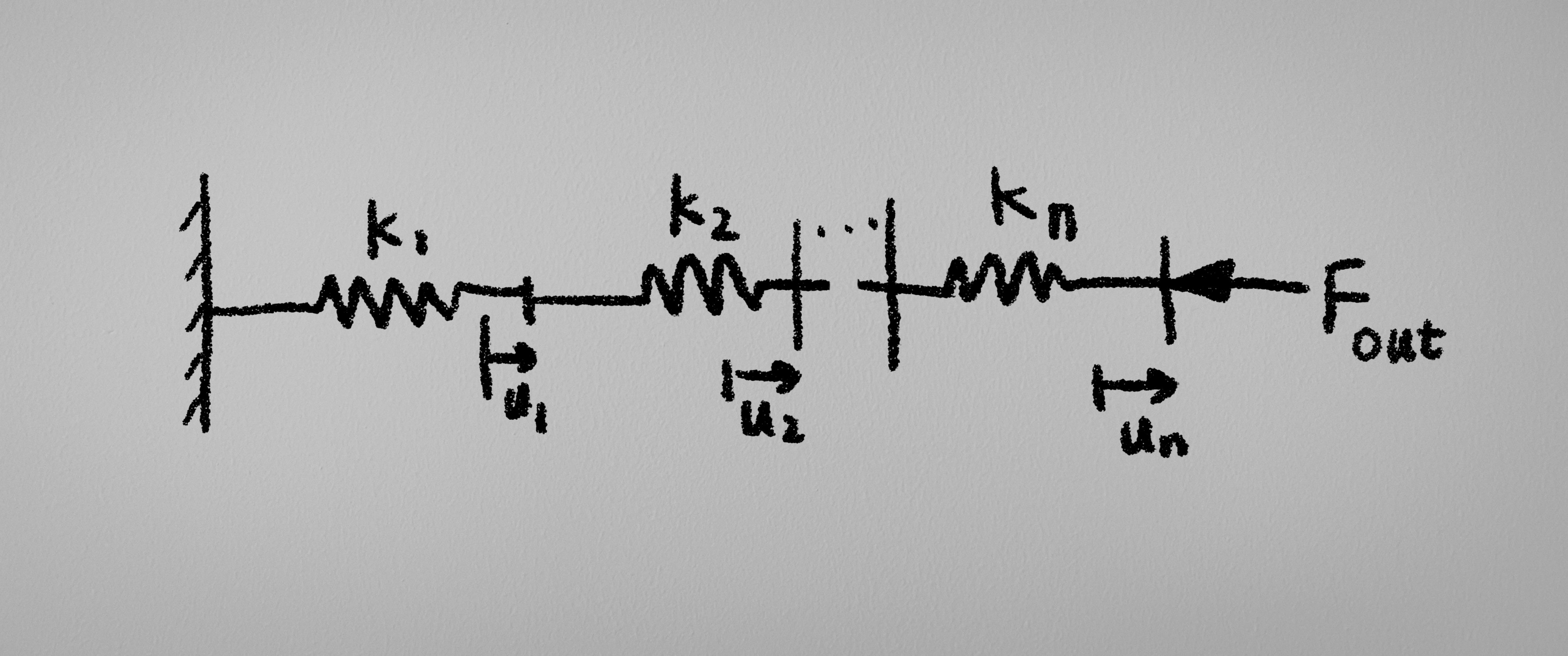
于是我们会说, 这些受力的方程为: (规定向右为正)
\[\left\{\begin{array}{lll}F_{墙} & = & - k (u_{墙} - u_1)\\F_1 & = & -k(u_1 - u_2)\\F_2 & = & -k(u_2 - u_3)\\ \cdots & = & \cdots\end{array}\right.\]但是对于每一个部分, 都有相互关联的成分:
\[\left\{\begin{array}{lll}F_{墙} & = & -F_1\\F_1 & = & -F_2\\F_2 & = & -F_3\\ \cdots & = & \cdots\end{array}\right.\]最后, 整体的平衡关系:
\[F_{墙} = - F_{out}\]于是我们就能够计算外力的分布了.
那么能不能再复杂一点?
没问题, 我们只需要将需要考虑的东西扩展一下, 比如说, 这个时候考虑一个在重力场中倒挂的弹簧.
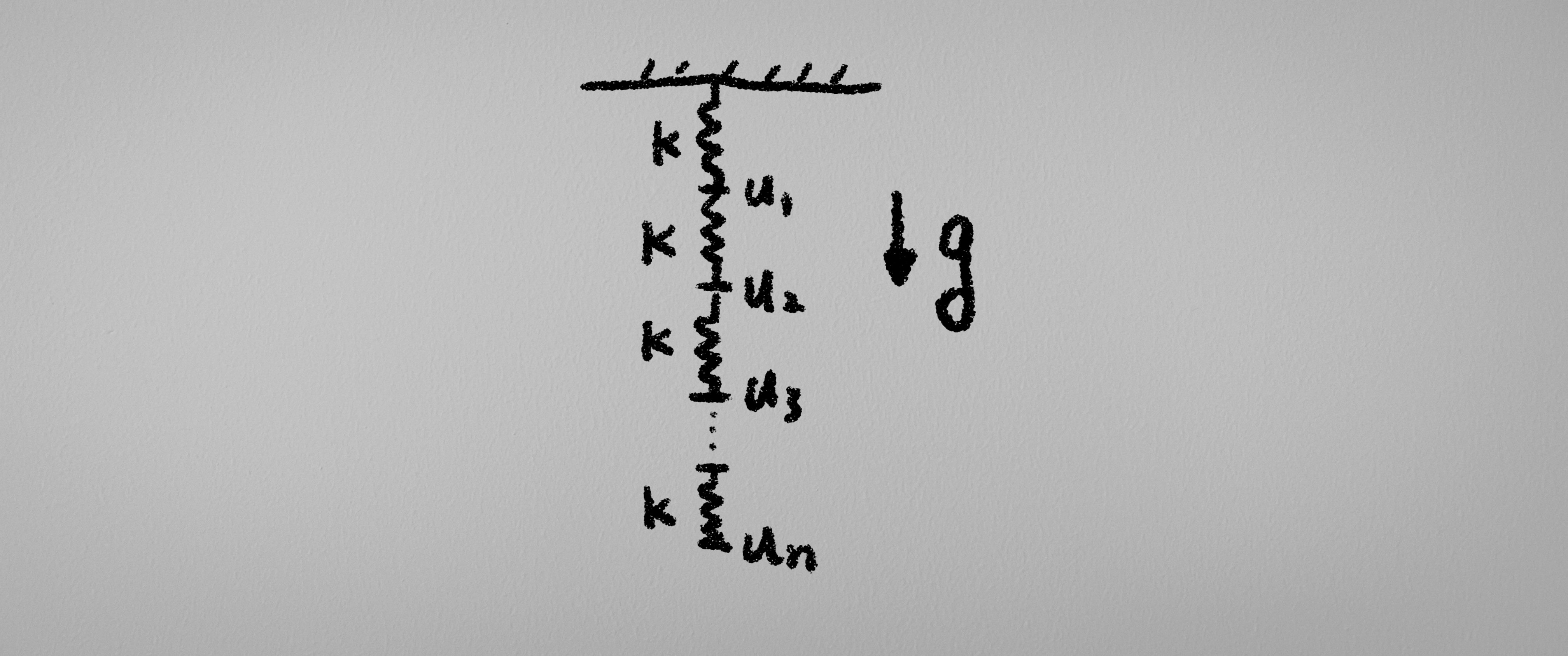
相较于之前的问题, 不难发现变化的只有受力的方程部分:
\[F_i = -k(u_i - u_{i+1}) + (n - i) \Delta m g, \Delta m = \frac{m}{n}\]于是就能够通过这样的方式来计算最终的解.
来点代码
先从最简单的一个点的弹簧平衡问题开始:
# ruby
K = 1 # 恢复系数
F_Out = 1 # 外力
ALLOWRANCE = 0.001 # 精度
displacement = 0 # 位移
force = F_Out - K * displacement # 合力
count = 0 # 收敛次数计数器
while force > ALLOWRANCE
displacement += force * 0.1 # 收敛的算法应该需要重写
force = F_Out - K * displacement # 合力
count += 1
end
puts displacement, count
# => 0.9990449950492033
# => 66上面那样的结果还是和实际的结果相吻合的. $\Delta x = \frac{F_{Out}}{K} = 1$, 误差在可以接受的范围内. 那么为什么不将这个简单的代码拓展到稍微复杂一点的问题呢?
那么首先是一个对上面的方法的更加"规范"的一个拓展. 用数学的公式来表述就是: $$\boldsymbol{F}_{net} = \boldsymbol{F}_{out} + \mathcal{K}\boldsymbol{u}_{displacement} = \left(\begin{array}{l}F_1\\F_2\\F_3\end{array}\right) + \left(\begin{array}{lll}-K & 0 & 0\\0 & -K & 0\\0 & 0 & -K\end{array}\right) \left(\begin{array}{l}u_1\\u_2\\u_3\end{array}\right) = \boldsymbol{0}$$
# ruby
require "matrix"
K = 1
ALLOWRANCE = 0.0001
K_Matrix = Matrix[
[-K, 0, 0],
[0, -K, 0],
[0, 0, -K]
]
F_Out = Matrix.column_vector([1, 0, 0])
displacement = Matrix.column_vector([0, 1, 0])
force = F_Out + K_Matrix * displacement
count = 0
while force.each.to_a.map{ |x| x**2 }.sum > ALLOWRANCE
displacement += force * 0.1 # 收敛的效果一般...
force = F_Out + K_Matrix * displacement
count += 1
end
puts displacement, count
# => Matrix[[0.9690968456173674], [0.0], [0.0]]
# => 33那么接下来, 考虑两个点之间的力. 这个时候我们可以用一个小技巧, 将两个点看作是一个物体的两个部分, 相互互为外界, 于是在数学上, 我们可以这样描述: $$\left\{\begin{array}{lll}\boldsymbol{F}_{out}^{(1)} + \mathcal{K}^{(1)}\boldsymbol{u}^{(1)} & = & 0\\\boldsymbol{F}_{out}^{(2)} + \mathcal{K}^{(2)}\boldsymbol{u}^{(2)} & = & 0\\\boldsymbol{F}_{out}^{(1)} + \boldsymbol{F}_{out}^{(1)} & = & 0\end{array}\right.$$
于是我们就能够得到: $$\boldsymbol{F}_{net} = \boldsymbol{F}_{Out} + \left(\begin{array}{llllll}-K & 0 & 0 & K & 0 & 0\\0 & -K & 0 & 0 & K & 0\\0 & 0 & -K & 0 & 0 & K\\0 & 0 & 0 & -K & 0 & 0\\0 & 0 & 0 & 0 & -K & 0\\0 & 0 & 0 & 0 & 0 & -K\end{array}\right)\left(\begin{array}{l}u_1^{(1)}\\u_2^{(1)}\\u_3^{(1)}\\u_1^{(2)}\\u_2^{(2)}\\u_3^{(2)}\end{array}\right) = \boldsymbol{0}$$
# ruby
require "matrix"
K = 1
ALLOWRANCE = 0.0001
K_Matrix = Matrix[
[-K, 0, 0, K, 0, 0],
[0, -K, 0, 0, K, 0],
[0, 0, -K, 0, 0, K],
[0, 0, 0, -K, 0, 0],
[0, 0, 0, 0, -K, 0],
[0, 0, 0, 0, 0, -K]
]
F_Out = Matrix.column_vector([0, 0, 0, 1, 0, 0])
displacement = Matrix.column_vector([0, 0, 0, 0, 0, 0])
force = F_Out + K_Matrix * displacement
count = 0
while force.each.to_a.map{ |x| x**2 }.sum > ALLOWRANCE
displacement += force * 0.1 # 收敛的效果一般...
force = F_Out + K_Matrix * displacement
count += 1
end
puts displacement, count
# => Matrix[[0.989519835930899], [0.0], [0.0], [0.9986899794913624], [0.0], [0.0]]
# => 63于是就能够通过引入更多的点来让这个问题进一步符合实际问题. 比如三个点的$\mathcal{K}$矩阵: $$\left(\begin{array}{lllllllll} -K_1 & 0 & 0 & K_2 & 0 & 0 & 0 & 0 & 0\\ 0 & -K_1 & 0 & 0 & K_2 & 0 & 0 & 0 & 0\\ 0 & 0 & -K_1 & 0 & 0 & K_2 & 0 & 0 & 0\\ 0 & 0 & 0 & -K_2 & 0 & 0 & K_3 & 0 & 0\\ 0 & 0 & 0 & 0 & -K_2 & 0 & 0 & K_3 & 0\\ 0 & 0 & 0 & 0 & 0 & -K_2 & 0 & 0 & K_3\\ 0 & 0 & 0 & 0 & 0 & 0 & -K_3 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -K_3 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -K_3 \end{array}\right)$$ 又或者是考虑更加复杂一些的$\mathcal{K}$的形式: $$\left(\begin{array}{lll} -K_{11} & -K_{12} & -K_{13}\\ -K_{21} & -K_{22} & -K_{23}\\ -K_{31} & -K_{32} & -K_{33} \end{array}\right)$$ 于是就可以表达更加复杂的弹性性质了. (容我好好学习一下弹性体力学... )
那一个立方体是不是…
在某种程度上来说, 我们可以通过一点点的拓展来将立方体看作是一种对上面的问题的Pro Max版本.
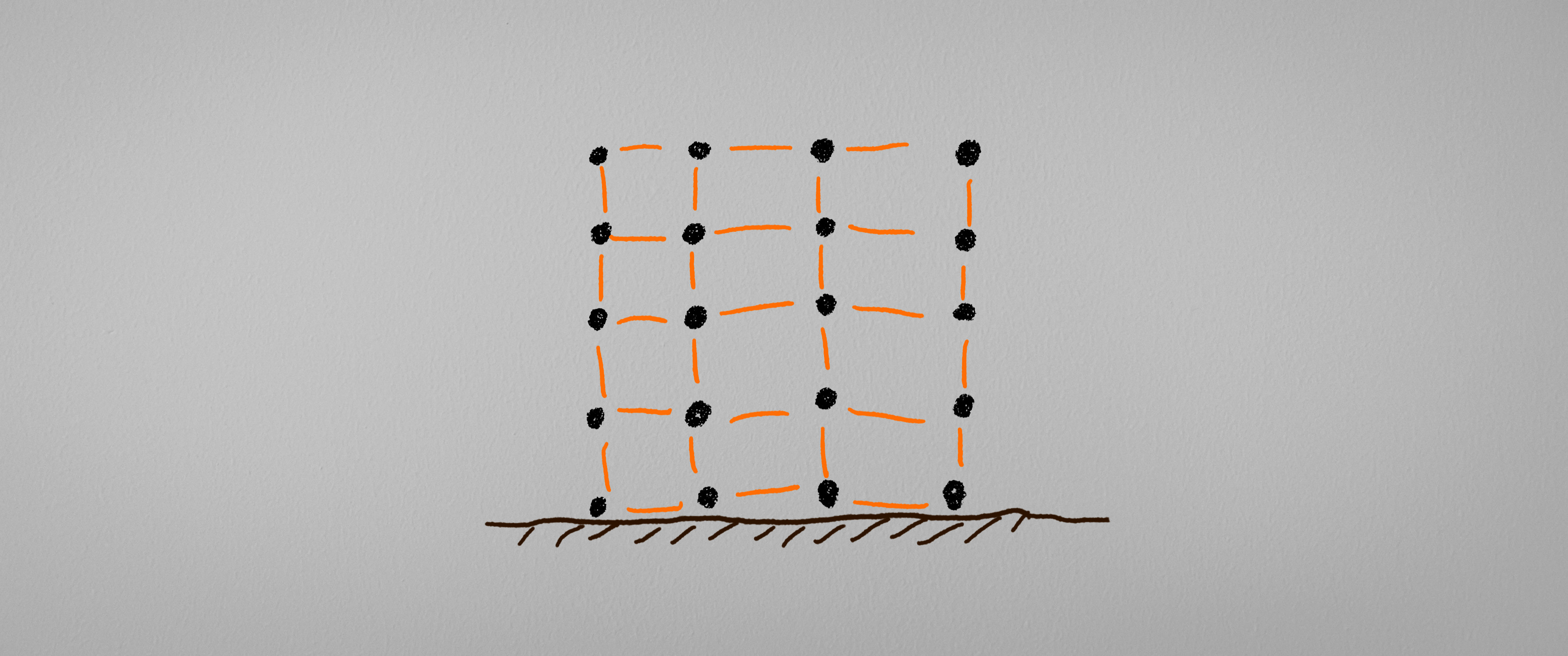
或者也可以用下面的图像:
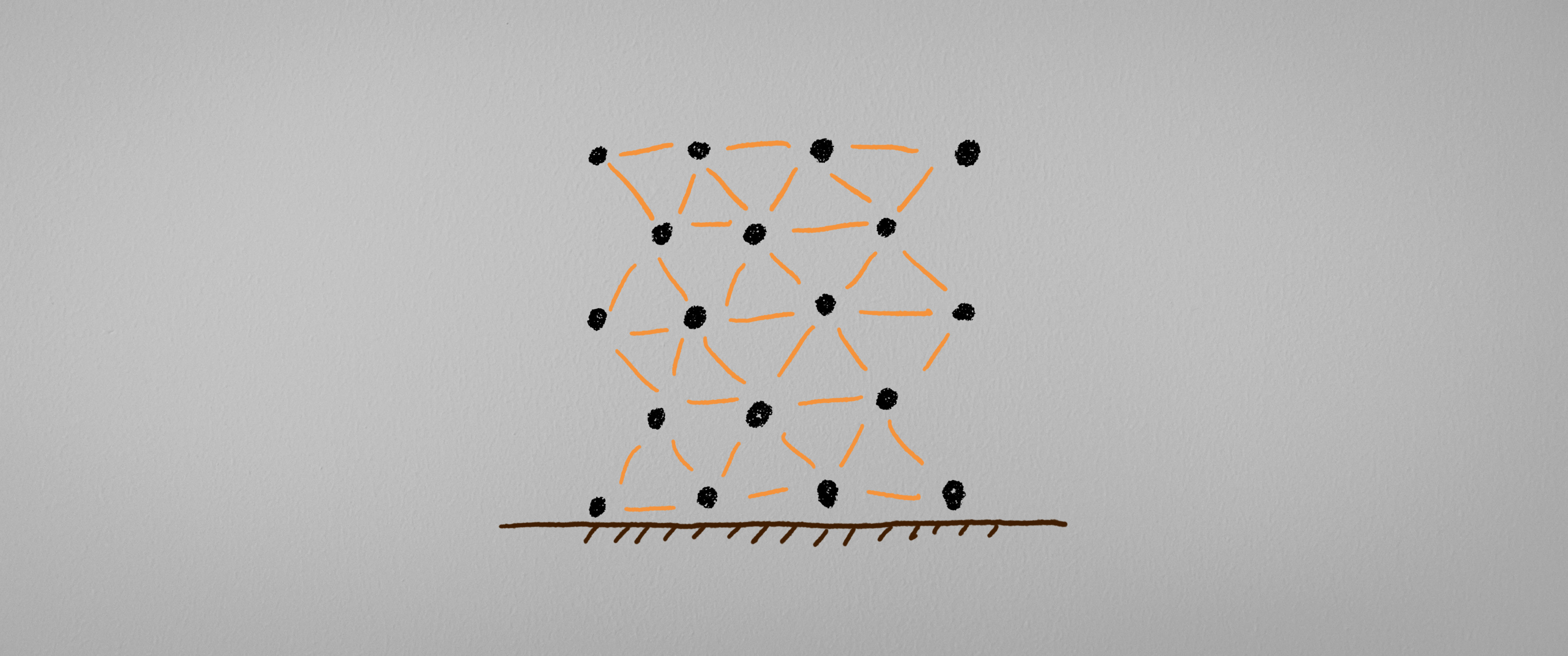
于是问题就变成了对上面的处理方法的”亿点”拓展了. 但是在上面的问题中, 需要计算的东西着实有些多了一些, 所以这个时候我们就可以应用计算机来辅助我们进行模拟计算. 并且我们还能够发现, 上面的计算过程中, 我们的特征点并不是像之前分析的那样: “在变化大的地方密集, 在变化小的地方稀疏”, 而是均匀的分布的, 这也同样是一种可以进行优化改进的地方.
这样的计算方式好像就叫做”有限元分析”. 但是名字不太重要, 我们的想法不过就是将原本复杂的连续的问题通过变成一个个的点(离散化)的方法来减少研究的规模, 来达到简化计算的目的. 总之你已经学会了$1+1$了, 那么为什么不试试看…
更加严格一点的说法
如果我们将$k$看作是一个线性映射$\mathcal{A}$, 将相对位移(用一个向量来表示)映射到物体的受力$\vec{f} = \mathcal{A}\delta\vec{r}$. (不过为了方便以后的区分, 将$\delta\vec{r}$记作$\vec{u}$, 这样方便一些. )
如果我们仅仅将物体看作是抽象的一根杆, 将相对位移看作是相对杆的延长或压缩. 而不同的杆子在连接点需要满足特定的方程. 于是我们就能够得到$\vec{f} = -k\vec{u}$, 即在物体内部的应力分布. 对于广义坐标, 我们同样也能够将其排成一组向量$\boldsymbol{u}$来代表位移量. 而如果仅仅只考虑线性的近似的话, 收到的力就是$\mathcal{k}\boldsymbol{u}$, 其中$\mathcal{k}$是一个类似于恢复系数的一个二阶张量.
如果仅考虑一根杆子: 端点的变化量(广义坐标的位移)可以有沿杆方向的伸缩, 垂直杆平面的一个位移, 以杆为中心的旋转. 于是一共有$4$自由度的坐标. 而二阶张量也就同时可以应用到这个坐标系统上... 譬如伸缩对应的胡克定律, 垂直平面对应的(切变)切胁强, 绕杆旋转(其实也是切变产生的)扭矩... 最终在端点由"受力"平衡方程得到稳定解. 这就是处理这种问题的一种思路了.
和质点的思路是一样的, 都是通过抽象简化来减少计算的难度. 而其中又可以通过合理的设置特征点和特征点之间的关系, 来将一个不方便求解的问题划归为一系列的可以求解的简单的方程组. 就像是葫芦娃救爷爷一样, 不过这回我们的思路是要击败葫芦娃 -- 只要把那座大山分成一个个的点击破就可以了.
后记
想要写这篇文章的一个动机就是想要参与一下政委学长说的科普文章撰写活动.
并且之前Simulate Physics的文章中夸下海口, 要在之后读完费曼的一篇关于计算机模拟物理的论文… (虽然中间为了狗过期末寄完全没有开始干活就是了), 最近稍微看了那么几页, 自以为是有所了解, 并且之前的物理模拟干的着实有些烂(文字写得乱七八糟的), 打算之后好好学点新的东西(比如算法和数据结构之类的)重新开始. 所以用这篇科普文章来总结之前的思路吧.
哦, 最后, 这个暑假估计又是一个摆烂的暑假, 所以… 前面立下的flag不知道能不能收回… (捂脸)
(嗯, 所以这写的是个啥? 烂… )