狭义相对论
只是一个简单的整理
因为之前学习狭义相对论的时候, 基本全部靠背公式, 所以对这个完全没感觉.
\[\gamma = \frac{1}{\sqrt{ 1 - ( \frac{v}{c} )^2} }\\ x' = \gamma ( x - v t )\\ y' = y\\ z' = z\\ t' = \gamma ( t - \frac{v x}{c^2} )\]泡利: Special Relativity is a closed case.
虽然感觉现在有点感觉了, 但是现在看到泡利的话还是很不爽.
泡利在小学就可以读狭义相对论了.
咳.
经典力学
什么是经典力学? 就是 所有满足伽利略变换不变性的性质.
好, 下一节. (不是)
(不, 其实的确就是这样, 赵爹课上说了, 言多必失, 这就是经典力学最好的表达方式, 并且我不久前听到了一个好说法:
It is only slightly overstating the case to say that physics is the study of symmetry.
– Philip Anderson (1972)
很难说这个说法很离谱, 但是现在想想感觉真有道理, 并且这样的说法还很有美感 – 我是指从物理上的美感来说. )
狭义相对论
和经典力学的定义相类比, 可以得到这样的对狭义相对论下的力学的定义: 所有满足洛伦兹变换不变性的性质.
好, 完事. (才怪啊! )
狭义相对论的一种直观一点的理解方法
两个前提
- 所有物理学现象对于惯性系都是等价的
- 光速不变
光信号
假设有两个惯性系$K$和$K’$, 并且在开始的时候$t=0$的时候, $t’=0$. 类似于设置一个共同的起点. 然后在$t=0$的时候放出一道光芒, 向四面八方射去.
假如在$K$系中有个魔法机器$P1$在$(x, y, z)$上, 一旦受到光照就会爆炸. 这个事件就是$E$. 显然, 会发现有下面的结论:
\[x^2 + y^2 + z^2 = c^2 t^2\]然后在$K’$系中的观察, 这个$P1$机器是在$(x’, y’, z’)$上, 在$t’$时候爆炸. 那么显然, 只要你不傻的话, 就可以自信地写下这样的结论:
\[x'^2 + y'^2 + z'^2 = c^2 t'^2\]于是会发现有下面的这样的结论:
不论在什么的坐标系下, 都有
\[s^2 = x^2 + y^2 + z^2 - c^2 t^2\]保持不变.
(实际上, 还存在着$s \neq 0$的情况, 但是我这样的解释不是很能解决这个. )
Boost
翻译成中文叫做递升.
正如前面所说的, $s^2 = x^2 + y^2 + z^2 - c^2 t^2$, 所以不如考虑这样的一个坐标系, 满足里面的”线段”长度就是 $s^2 = x^2 + y^2 + z^2 - c^2 t^2$, 那么不难说, 这个坐标系在洛伦兹变换的时候就满足这个线段长度是不变的.
根据上面的这个朴素想法, 显然, 可以将原来的直角坐标系的概念小小地改变为四维的坐标, 每个坐标分量分别是$x, y, z, i c t$, 于是根据简单的”勾股定理”, 就可以得到线段长度的概念. (其中$i$为虚数)
最后, 考虑在$K$系中的点$(x,y,z,t)$, 而相对于另外一个坐标系$K’$中的点$(x’, y’, z’, t’)$, 他们相对于原点的”距离”$s$应该都是一样的, 那不妨将这两个坐标系的原点平移到一起, 然后自然的想法是, 因为这两个点应该是不同的坐标, (显然, 假如是一样的话, 那么不就是相当于根本没有变化嘛) 但是又有线段长度相等, 于是自然地就会联想到一个圆上的点 – 换句话说就是, 假如我们把这个点固定的话, 就好像是这个坐标系在旋转. 就像下图所画的一样:
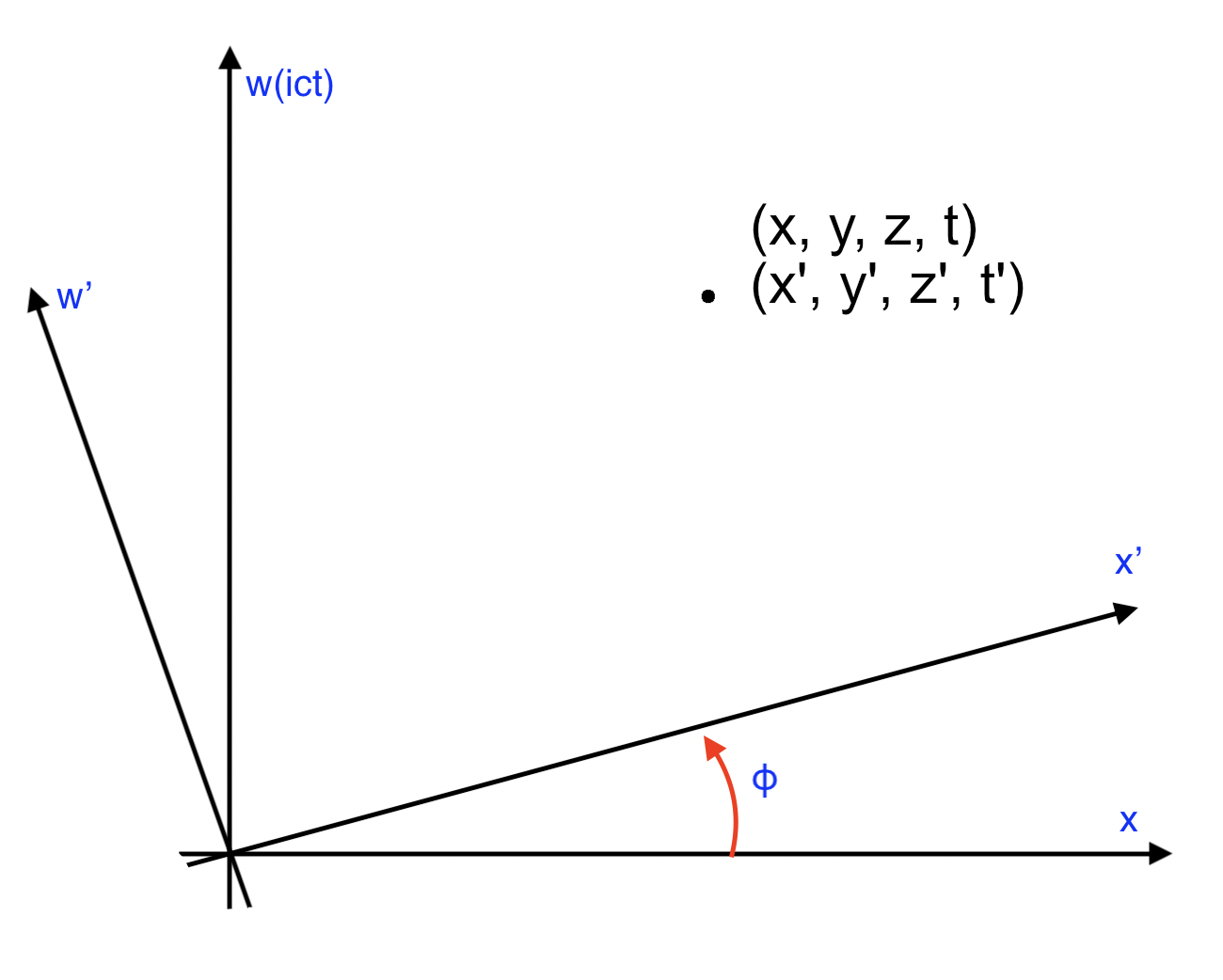
于是不妨设这个旋转的角度为$\phi$, 所以写出坐标之间的变换关系:
\[\left(\begin{array}{l} x\\ \omega \end{array}\right) = \left( \begin{array}{ll} \cos \phi & - \sin \phi \\ \sin \phi & \cos \phi \end{array} \right) \left(\begin{array}{l} x'\\ \omega' \end{array}\right)\](其中$\omega$就是$i c t$的简记. )
对于上面的点因为可以随便选择, 所以不妨令$x’$变成$0$, 那么就会发现
\[\left\{\begin{array}{l} x = - \omega' \sin \phi \\ \omega = \omega' \cos \phi \end{array}\right.\]简单计算就可以得到$\tan \phi = - \frac{x}{\omega}$, 所以用这样计算得到的$\phi$的三角函数关系:
\[\left\{ \begin{array}{l} \sin \phi = \frac{\frac{x}{\omega}}{\sqrt{1 + (\frac{x}{\omega})^2}} \\ \cos \phi = \frac{1}{\sqrt{1 + (\frac{x}{\omega})^2}}\end{array}\right.\]但是思考一下, 和$x’=0$所对应的$x$代表什么? 不就是$K’$系的坐标原点相对于$K$系的运动嘛, 于是$x = u t$, 那么就有$\frac{x}{\omega}=-i\frac{u}{c}$.
最后代入到原来的方程, 就会发现就得到了原来的变换关系.
最后就得到了洛伦兹变换.
\[\gamma = \frac{1}{\sqrt{ 1 - ( \frac{v}{c} )^2} }\\ x' = \gamma ( x - v t )\\ y' = y\\ z' = z\\ t' = \gamma ( t - \frac{v x}{c^2} )\]最后
嗯, 还是有点没有清楚, 但是有一个变换不变量. 嗯, 其他的以后再说.
补充
假如只有惯性系, 我上面的$ict$的理解方法是可以使用的.
但是假如到了广义相对论的情况下, 就会出现一些奇奇怪怪的问题, 就是这样的操作会导致出问题. (具体现在还不是很懂…)
等我以后再学深一点…
注: 这样的操作实际上是做了一个复数扩张, 就是假定了变换都是实李群, 但是还会遇到其他奇怪的东西. 比如复数的情况下, 这样”转”的操作就会遇到奇点, 那么就要加上流数. 或者是在引入$i c t$后, 洛伦兹变换的$I,P,T, PT$的区域就会混在一起… (我佛了).