Overview

计数率, 误差, 数据分析

感觉缺少一门专门讲误差分析, 实验测量的专业课程. 并且还得是物理方向的, 而非数学方向的, 或者是计算机方向的概率论课程类似的课程.

虽然好像 Mathematica 的 Around 函数用起来很香, 但是不得不承认, 感觉不够.

分布
简单理解就是 Landau 分布是因为 $δ$ 电子带走了部分的原初粒子能量; 且原初粒子的能量并没有完全沉积在探测器中.
- Landau 分布: 薄介质 (灵敏体积有限无法完全沉积)
- Gauss 分布: 厚介质 (完全沉积)
- 分布的叠加: (用 $l_{Δ E_p} ≈ \frac{1}{\sqrt{2 π}} \mathrm{e}^{- \frac{1}{2} (λ + \mathrm{e}^{-λ})}$ , ( $λ = \frac{Δ E - Δ E_p}{ξ}$ , $Δ E_p$ 为最概然能损) 表示 Landau 分布, $g_{μ, σ}$ 表示 Gauss 分布)
  - $g_{μ_1, σ_1} * g_{μ_2, σ_2} = g_{μ_1 + μ_2, \sqrt{σ_1^2 + σ_2^2}}$
计数率: 真实计数率 $n_0$ , 实际计数率 $n$ , 分辨时间 (死时间) $τ$ : $n_0 = \frac{n}{1 - n τ}$ .
探测效率: 粒子单次进入探测器被探测到的概率 $p =$ 记录到的 / 入射的.
分辨率: 一般用 $2.354 σ$ 半高宽来表示
对于计数 (泊松分布 $→$ 高斯分布) 测量值 $N$ , 统计误差可以用 $σ = \sqrt{N}$ 表示.
误差的累积计算: $f(a ± σ_a, b ± σ_b) = f(a, b) ± \sqrt{(∂_a f σ_a)^2 + (∂_b f σ_b)^2}$
计数误差在实验中的应用
- $Δ t$ 时间内测量到 $N$ 个计数, 计数率: $n = \frac{N}{Δ t} ± \frac{\sqrt{N}}{Δ t}$
- 相对误差 $δ = \frac{σ}{N} = \frac{1}{\sqrt{N}}$ , 测量精度好于 $1 \%$ (误差小于 $1 \%$ ), 则需要时间 $\sqrt{n t} > 100$
- 测量时间分配 (本底 $n_{\mathrm{b}}$ 与样本 $n_{\mathrm{s}} - n_{\mathrm{b}}$ )
  - 相对误差 $δ = \sqrt{\frac{n_{\mathrm{s}}}{t_{\mathrm{s}}} + \frac{n_{\mathrm{b}}}{}}$
我逐渐理解一切 (并没有)
所有的实验 (大部分) 都是在进行一个计数 (并不是, 比如 ADC 的道数其实反应的是强度), 这些计数反应了一个物理量的强度 (一般都是通过侧面反应的, 比如通过电离原初电子离子对, 或者是放大, 或者是收集 Cherenkov 光子等, 都是通过计数的方式实现的.
那么在测量的时候由于计数的统计上的误差, 就会成为一个实验误差的来源.

计数满足的是一个 Poisson 分布, (在 $N → ∞$ 时逼近 Gauss), 于是分析计数的统计规律的时候就变成了分析 Poisson 分布的统计规律了.

气体探测器

对应物理过程为电离过程 (电离能损 $n = \frac{Δ E}{W}$ ), 通过外加电场实现对电离得到的电子, 离子的漂移 (倍增等过程), 通过漂移电荷在读出 pad 上的电荷重新分布产生的电流, 从而读出电流信号.

根据外加的电场的大小会工作在不同的区域.

Basic

反应截面 $σ$ 和平均自由程 $λ = 1 / ρ σ$
单位长度里面发生 $n$ 次碰撞的概率 $\mathrm{Poisson}(L / λ, n)$
平均电离能 $W$ : 产生 1 个自由电子需要的能量, 用于计算原初电离电子/离子对
混合物: $W = ∑ w_i W_i$
- 原初电离
- 总电离
平均碰撞次数: $\left\langle N \right\rangle = \left\langle \mathrm{d} E \right\rangle / W$
漂移速度 $μ = \frac{e E}{m N σ} \sqrt{\frac{η}{2}}$ : 通过调节混合气体比例改变 $\sqrt{η} / σ$ , 用于计算漂移信号时间
一般电子是阳离子的数千倍.
横向扩散: 可以通过施加磁场抑制扩散

不同场强下的电子/离子:

电势差 (指数)	0 ~ 1	1 ~ 3	4 ~ 5	5 ~ 6	> 6
名称	复合	电离	正比	有限正比	盖格区/流光
行为	吸附/复合	漂移/扩散	漂移/扩散/电离	漂移/扩散/电离	漂移/扩散/电离/光电
电子/离子对关系	复合	饱和 = 原初电离	$\propto$ 原初电离		与入射粒子沉积能量无关

电离区

探测器	能量	动量	位置	时间
电离室	和脉冲高度相关			测量得到的时间减去漂移时间

电离室

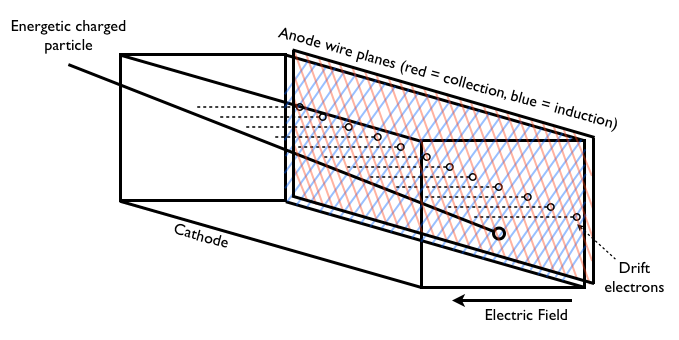
/_img/particle-detector/RealSchematicTPC.png

(漂移室示意图, 图片来源 Wikipedia)

利用原初电子漂移的信号进行测量.

信号极性

正极板: 正电荷从地流向电极, 负电荷从电极流向地, 空间中电子靠近, 负信号
负极板: 正电荷从电极流向地, 负电荷从地流向电极, 空间中离子靠近, 正信号

信号为两个矩形信号 (短: 电子; 长: 离子) 的合成
探测效率影响因素:
- 甄别阈值
- 光子/中子等不是直接探测, 而是先反应, 变成带电次级粒子才能探测, 有一个相互作用的截面转换效率
饱和特性: 输出脉冲电荷量与工作电压 (在饱和电压厚不变, 电离区)
坪特性: 输出脉冲数 (计数率) 随电压升高 - 然后饱和 (同上)

脉冲型电离室

过微分电路变成脉冲

电流型电离室

记录大量入射粒子引起的总电离电流
计算饱和电流值
- 电离损失能量 $E_{\mathrm{ion}}$
- 平均电离能 $W$
- 电离电子离子对 $\frac{E_{\mathrm{ion}}}{W}$
- 源流强 $f$
- 饱和电流 $f \frac{E_{\mathrm{ion}}}{W}$

正比区

产生的电子离子对数量和原初电离数目成正比, 一般有增益系数 $M = \frac{N}{N_0}$ . 改变平面室结构为丝室结构来取得更大的电场, 非丝区域可以作为漂移室进行测量.

探测器	能量	动量	位置	时间
正比计数器 (稻草管)	信号电荷量正比原初总电离	一般	交错, 单根否	到达时间
多丝正比室	同正比, 阴极面或阳极丝之和	一般	同正比	同正比
多丝漂移室	可	径迹拟合	可	可
时间投影室	可	径迹	可	可

其他

一般有增益系数 $M \propto \mathrm{e}^{C V_0}$ 和工作电压有指数关系
但是增益是有上限的, $M = \frac{M_0}{1 - γ M_0}$

正比计数器 (稻草管 StrawTube)

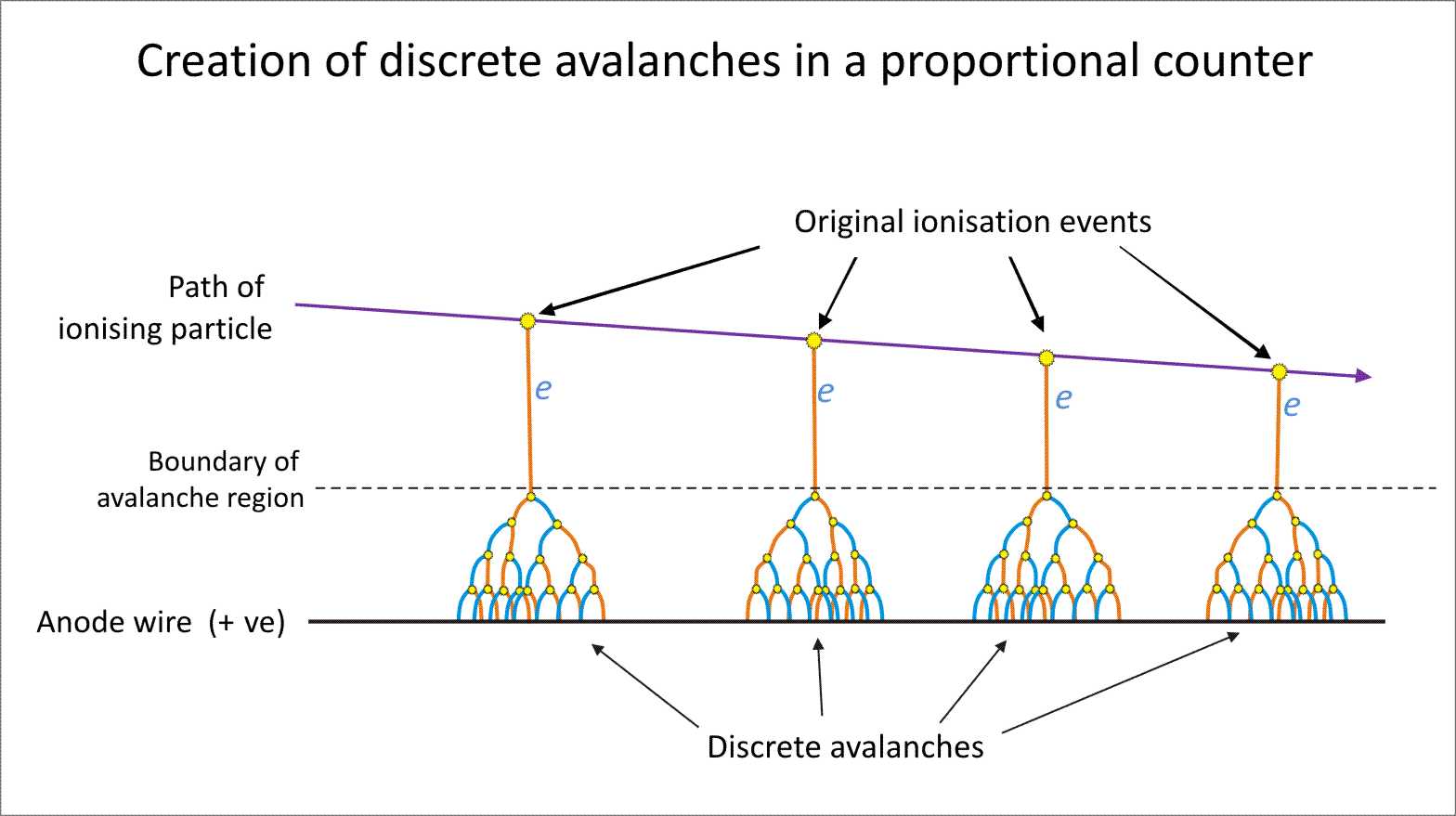
/_img/particle-detector/Proportional_counter_avalanches.jpg

(信号丝示意图, 图片来源 Wikipedia)

因为电场不是均匀的, 所以漂移的信号并不是矩形, 且会有两部分组成: 电子的漂移 (时间短, 幅值大), 离子的漂移 (信号长, 幅值小).

核心部件为丝室:

丝室气体增益: $M = ∑ M_0^n γ^{n-1} = \frac{M_0}{1 - γ M_0}$
( $M_0$ 为气体放大倍数, $γ$ 为雪崩电子产生光电子的概率)

为了防止放电, 需要抑制 $γ$ :
- 假如多原子分子吸收光子
- 增大信号丝表面逸出功
能量分辨:
时间分辨: 入射粒子的位置, 角度, 漂移速度的晃动, 漂移时间, 电子学…
空间分辨: $\frac{2 r}{\sqrt{12}}$ ( $r$ 为半径)
分辨时间 $τ$ : 和输出脉冲宽度有关 (分辨一个计数事例所需要的时间)
分辨时间和计数率
- 分辨时间 $τ$ 和实际计数率
探测效率:
探测效率的计算
- 计算平均电离: $\left\langle N \right\rangle = (\mathrm{d} E / \mathrm{d} x) \left\langle L \right\rangle / W$
  $\left\langle L \right\rangle$ 为平均经过介质的距离.
- 电子学噪声 $c_{\mathrm{noise}}$
- 探测效率 $\frac{M \left\langle N \right\rangle}{M \left\langle N \right\rangle + c_{\mathrm{noise}}}$

多丝正比室 MWPC

将单个稻草管换成漂移区 (灵敏区) 和倍增区.

2 维 XY 测量:
- 交叉 X/Y 放置的信号丝
- 阴极读出 pad 可以与丝垂直, 感应读出信号
- 可以通过电阻分配原理进行双端读出
能量分辨: 分辨能量
- 本征分辨: 原初总电离涨落 + 气体增益
- 机械, 电气公差
- 粒子斜入射的时候单根阳极丝无法代表, 需要将阳极丝的信号综合在一起
时间分辨: 分辨入射粒子的入射时刻
分辨时间: 影响最大计数能力
空间分辨: $σ / \sqrt{12}$
探测效率: 带电粒子 (一般是 MIP) 通过探测器被记录到的概率

多丝漂移室 MWDC

在多丝正比室的基础上信号丝之间加上场丝来调节电场使得电场更加均匀.

动量测量: 通过漂移室的径迹进行拟合 (配合磁场) $R = \frac{10}{3} \frac{p_{\mathrm{T} [ \mathrm{GeV} / \mathrm{c} ]}}{B [ \mathrm{T} ]}$ 测量动量
动量的分辨主要来源于:
- 位置分辨: $\frac{σ_{p_{\mathrm{T}}}}{p_{\mathrm{T}}} = σ_x \frac{p_{\mathrm{T}}}{0.3 B L_{\mathrm{T}}^2} \sqrt{\frac{720}{N + 5}}$
- 多次散射: $\frac{σ_{p_{\mathrm{T}}}}{p_{\mathrm{T}}} ≈ \frac{0.052}{B × L_{\mathrm{T}}} \frac{1}{β} \frac{p_{\mathrm{T}}}{p} \sqrt{\frac{L}{X_0}}$
  对于动量低的粒子为主要影响
  
  通过使用 He 为主的工作气体, 使用 Al 丝作为场丝来减少室内物质量来减少库仑散射
粒子鉴别: 通过 $Δ E / Δ x$ 来鉴别
顶点测量:
漂移室老化: Malter 效应 (因为放电在场丝上生长长链聚合物, 导致放电)

时间投影室 TPC

类似电离室, 通过电子离子的漂移产生的信号进行读出. 通过场笼实现漂移电场的均匀性, 并通过 Ion gate 实现抑制阳离子回流.

激光标定: 用激光产生原初电离, 然后观察漂移时间
阳离子回流导致的电场畸变:
- 原初电子/离子对流强 $f_0 = f_{\mathrm{comp}} ⋅ E_{\mathrm{comp}} / W_0$
  $f_{\mathrm{comp}}$ 组分的流强, $E_{\mathrm{comp}}$ 组分的能量, $W_{0}$ 电离能损, 对于宇宙线, 这个流强约 $f_0 ≈ 10^6 \mathrm{s}^{-1} \mathrm{m}^{-3}$ .
- 电子运动速度快, 剩下的阳离子会产生电场, 阳离子浓度 $ρ_+ = f_0 L / (v_{e^-} - v_+)$
  $v_{e^-}$ 为电子漂移速度, $L$ 为漂移室腔体长度
- 可以利用高斯定理计算 $E_r ∼ r - \frac{1}{r}$ 的形式 (圆柱的径向电场, 对原电场的畸变)
- 可以通过离子门 (ions gate) 实现抑制回流

放电区, 流光区

火花室

平行极板间的电场强度在 $E ∼ 20 \mathrm{kV} / \mathrm{cm}$ , 通过闪烁体探测器接受火花室的流光信号.

雪崩平行板室 PPC/PPAC

在平板间加高电压, 但是因为被击穿后需要重新充电, 恢复时间长, 所以信号计数率低.

阻性板室 RPC

将平行板室的金属电极换成带电阻的电极, 这样就变成局部击穿, 恢复时间快.

可以工作在雪崩模式和流光模式.

电离室和 RPC 相比, 电离室信号更大
流光模式快信号 Q 大且占的比例更大 (相比雪崩模式)

多气隙阻性板室 MRPC

将单气隙变成多气隙.

窄气隙: 信号小, 多个窄气隙叠加, 电极信号为和, 统计涨落更小

其他

感觉更像是如何通过构造 “场丝” 的几何形状, 来想办法减少物质量 (减少散射), 获得较好的电场结构 (均匀电场), 以及增加探测效率的操作.

目标: 响应时间更快, 空间探测颗粒度更小

微电极 MSGC
- pros: 阳极条和阴极条并排, 位置分辨率高
- cons: 正离子在表面堆积局部放电
GEM, Thick GEM
- pros:
  - 微通孔结构, 密电场的同时兼有屏蔽功能 (正离子对信号没有贡献), 通过多层 GEM 结构可以提高探测效率;
  - 漂移距离短 (相对 GEM 和读出 pad), 信号持续时间短 (分辨用时短), 计数率高
- cons: GEM 软, 需要固定, 改进: THGEM 硬

半导体探测器

和气体探测器类似, 但是因为半导体本身的漂移会产生很大的本底信号, 所以需要想办法抑制 (降温, 利用 PN 结构造反向电场/耗尽层).

原理

$1 \mathrm{μ m}$ 的硅的沉积能量 $∼ 400 \mathrm{eV} / \mathrm{μ m}$
本征半导体: 理想不含杂质的半导体
载流子: 电子和空穴的统称
- 本征载流子的估算: $ρ_{\mathrm{Si}} \mathrm{e}^{- E_{\mathrm{g}}^{\mathrm{Si}} / 2 k T}$ , $E_{\mathrm{g}}^{\mathrm{Si}} = 1.1 \mathrm{eV}$
  所以可以通过降温的方法来减少本征载流子, 也可以通过增加耗尽层来抑制本征载流子
  - 耗尽层: $d ≈ x_p ≈ \sqrt{\frac{2 ε U}{e N_{\mathrm{A}}}}$
- 杂质半导体:
  - 电子 $×$ 空穴浓度不依赖于杂质浓度, 若引入少量杂质使得 $n$ 变大, 则 $p$ 减少
  - 施主杂质: 把电子贡献给导带的杂质, 对应能级为施主能级, 位于导带底部
  - 受主杂质: 能接受满带中电子产生导电空穴的杂质, 对应能级为受主能级
  - 多数载流子: 占多数的载流子 (施主能级为主的为 N 型, 反之为 P 型); 反之为少数载流子
- 非平衡载流子: 入射粒子在半导体内产生的载流子 (类似气体电离)
- 载流子迁移率: $μ = \frac{e E}{m} τ \propto E$
- 载流子电导率: $ρ = \frac{E}{j} = \frac{1}{e (n ⋅ μ_n + p ⋅ μ_p)}$
Fano 法诺因子 $F$ (影响 $σ = \sqrt{F E W}$ )
信号的产生:
- 耗尽层中的电场非均匀 (线性变化), 所以漂移速度是变化的

对半导体探测器的要求

物理要求	材料要求
电荷收集效率高, 能量分辨好	$L_{\mathrm{n, p}}$ 大或者 $τ_{\mathrm{n, p}}$ 大
工作温度高 (本底噪声小), 抗辐照性能好	$E_{\mathrm{g}}$ 大
灵敏区厚度大 (探测死区小)	杂质浓度低
$γ$ 射线探测效率高	原子序数大 (散射截面大)
可大量生产	材料/加工工艺

测量

能量分辨

$E = W ⋅ N$ , $E$ 为沉积的能量
- 能量分辨: $η = \frac{Δ E}{E} = 2.35 \frac{σ_E}{E}$
  $σ_E = \sqrt{F ⋅ E ⋅ W}$ , $F$ 为法诺因子
反康
影响能量分辨:

空间分辨

位置分辨与条宽 $Δ$ : $\frac{Δ}{\sqrt{12}}$
影响空间分辨:
- 原初电离展宽 ( $δ$ 电子使得原初电离电荷分布形状的偏离)
- 扩散
- 串扰: 相邻收集单元有电容耦合导致信号串扰 (半导体探测器的结电容模型)
- 读出单元上的噪声
- 重建算法:
  - 0-1 读出: $σ = \frac{Δ}{\sqrt{12}}$
  - 重心法: $σ_x^2 = σ_n^2 \left[ (∑_{i = 1}^N x_i^2) + N \left\langle x^2 \right\rangle \right]$
硅微条
硅像素
硅漂移

光探测

SiPM
- 分辨不服从 $\sqrt{n}$
  因为是多个像素组成, 单个像素导通后就对后续的导通不灵敏了.
雪崩二极管 APD:
- 利用倍增过程 (电气击穿) 对信号进行放大
硅光电倍增管 SiPM (盖格模式雪崩光电二极管 G-APD)

闪烁体探测器

结构

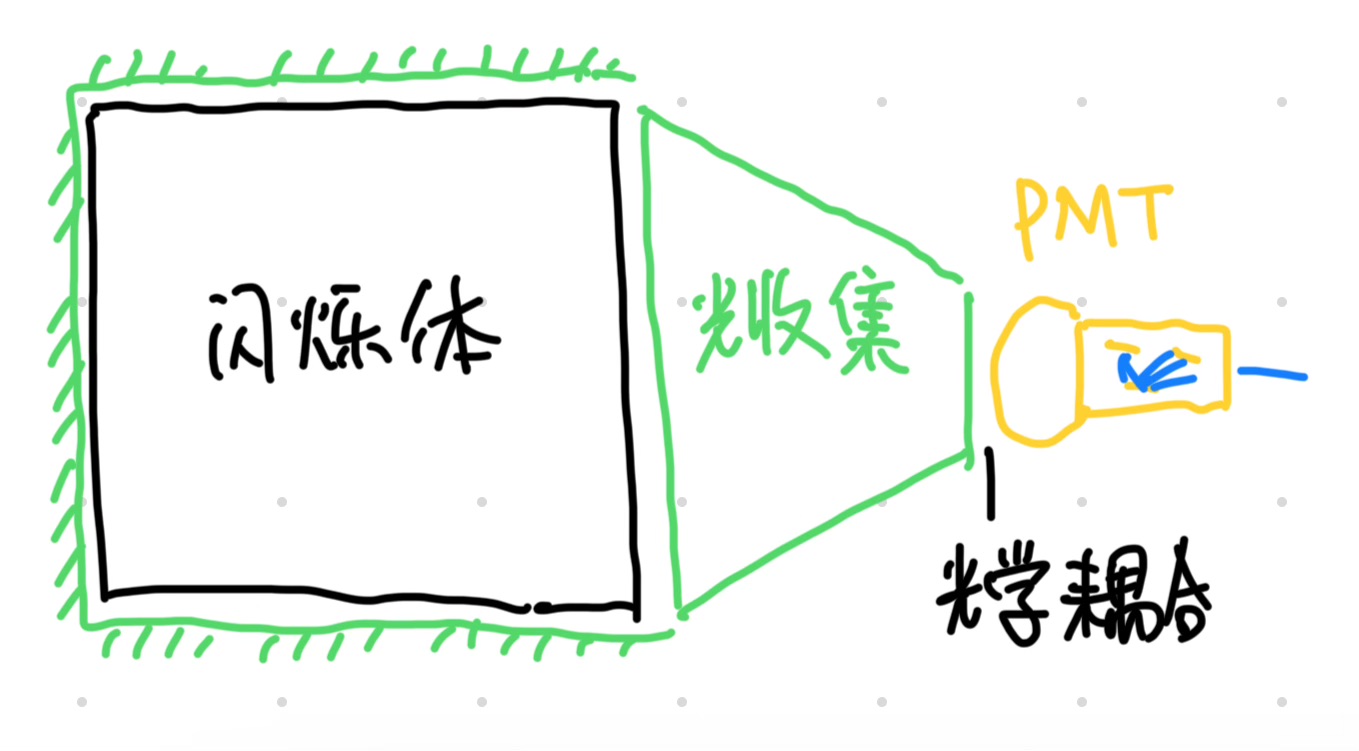
/_img/particle-detector/scintillation-detector.jpg

闪烁体

沉积能量 $\frac{\mathrm{d} E}{\mathrm{d} x}$ 以光的形式发射
光产额: 闪烁体中损失能量中被转换为光子输出的比例
发光衰减时间 $τ$ : $I(t) = I_0 \mathrm{e}^{- t / τ}$
闪烁体发光是要一段时间的 (相比 Cherenkov 的几乎瞬间)
衰减长度: 闪烁光在闪烁体内传播时, 光衰减到初始时 $1 / e$ 所走过的距离
- 本征衰减长度, 技术衰减长度
探测效率: 粒子在闪烁体内产生脉冲信号与入射粒子数之比
温度效应: 闪烁体性能随温度的变化
辐照效应: 闪烁体性能
闪烁发光效率:
- 光输出 $S$ : 一次闪烁过程中光子数目和入射粒子在闪烁体中损失能量 $Δ E$ 之比
- 能量转换效率 $P$ : 光子总能量和入射粒子损失能量之比
闪烁发光效率计算
- $P = \frac{Δ E}{n_{h ν} h \left\langle ν \right\rangle}$ 一般可以用平均波长来计算
闪烁体的体积和闪烁体能谱
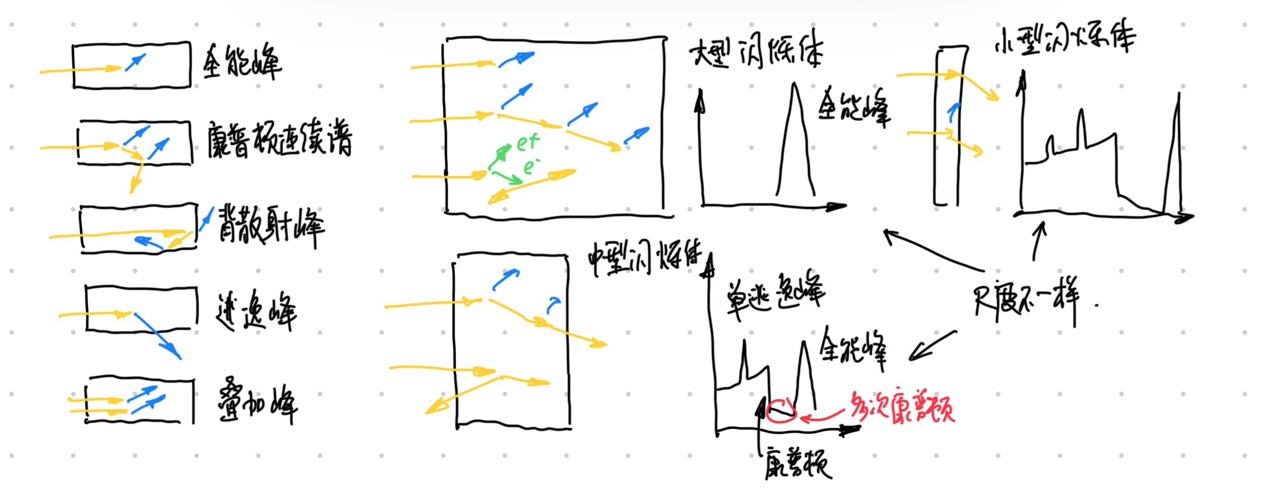
- 全能峰: 光电效应 + 电子对 + 康普顿
- 康普顿连续谱: 非单能的电子反冲
- 背散射峰: 大角度康普顿散射, 形成背散射峰 (能量接近 $200 \mathrm{keV}$ )
- 逃逸峰: 次级电子, 湮灭 $γ$ 子, X-ray 逃逸 (比康普顿沿要远)
- 叠加峰: 两个 $γ$ 同时进入
- X 射线峰: 周围物质和 $γ$ 的相互作用 (一个解决方法就是放 $Z$ 小的在周围)

光电倍增管 PMT

能量分辨公式: $n = 2.354 \sqrt{\frac{1}{N} (1 + \frac{δ}{δ_1 (δ - 1)})}$
多光子分辨: Gauss 卷积

应用

触发计数

过阈甄别
探测效率: 多重符合 (用来挑出真信号) 测量探测效率

定时测量

甄别阈值
双阈甄别
过零定时
恒比定时
Q/T 修正

能量测量

全吸收
取样量能器

切伦科夫探测器

原理

切伦科夫辐射特点
- 方向性: $cos θ_{\mathrm{c}}(λ) = \frac{1}{n(λ) β}$
- 阈速度: $β_{\mathrm{T}} = \frac{1}{n(λ)}$
- 最大辐射角: $θ_{\mathrm{max}} = cos^{-1} \frac{1}{n}$
- 辐射光谱: $\frac{\mathrm{d}^2 N}{\mathrm{d} λ \mathrm{d} x} = \frac{2 π α z^2}{λ^2} sin^2 θ_{\mathrm{c}}$
- 辐射光子数: $N \frac{2 π z^2}{137} sin^2 θ \left( \frac{1}{λ_2} - \frac{1}{λ_1} \right)$
  可见光的结论: $N ≈ 490 sin^2 θ$
- 发光时间: 几乎不存在延时
- 偏振性: 平面偏振光
光收集
- 球面镜
- 全反射
Cherenkov 探测类型
- 计数器 (脉冲型, 累积型)
- 径迹探测器
- 量能器
- 粒子鉴别器

Cherenkov 粒子鉴别器

阈式 Cherenkov

原理:
- 切伦科夫光子数 $N_{\mathrm{pe}} = L sin^2 θ N_0$
- 光子数服从 $N_{\mathrm{pe}}$ 的 Poisson 分布, 探测效率 $ε_{\mathrm{eff}} = 1 - \mathrm{e}^{- N_{\mathrm{pe}}}$
- 对于相同动量 $p$ 的不同质量粒子, 则可以根据光子数去分辨粒子种类
速度分辨: $\frac{Δ β}{β} = \frac{(m_2^2 - m_1^2) ⋅ c^2}{2 p^2}$

成像式

RICH

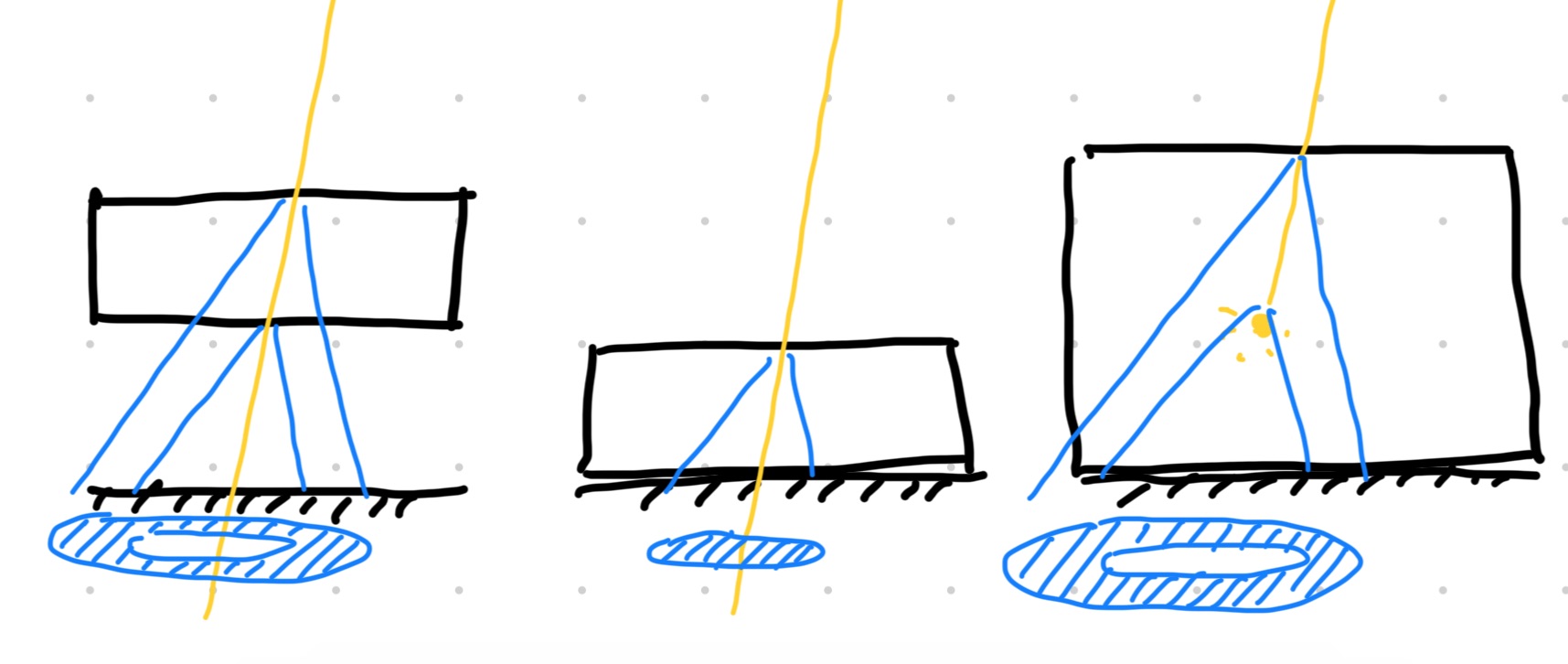
为什么是 Ring (环): 探测器和 Cherenkov 辐射体之间有一段 “飞行” 距离
以及为什么不是环 (ICE-CUBE): 探测器和 Cherenkov 是在一起的, 粒子一直走到探测器表面.

以及为什么还是环 (神冈): 粒子行进距离有限, 走不到尽头就 “没了”
误差来源
- 入射粒子晃动
- 同一波长的展宽
- 探测器空间分辨
- 色散 (FARICH 通过不同折射率来消除色散)

DIRC

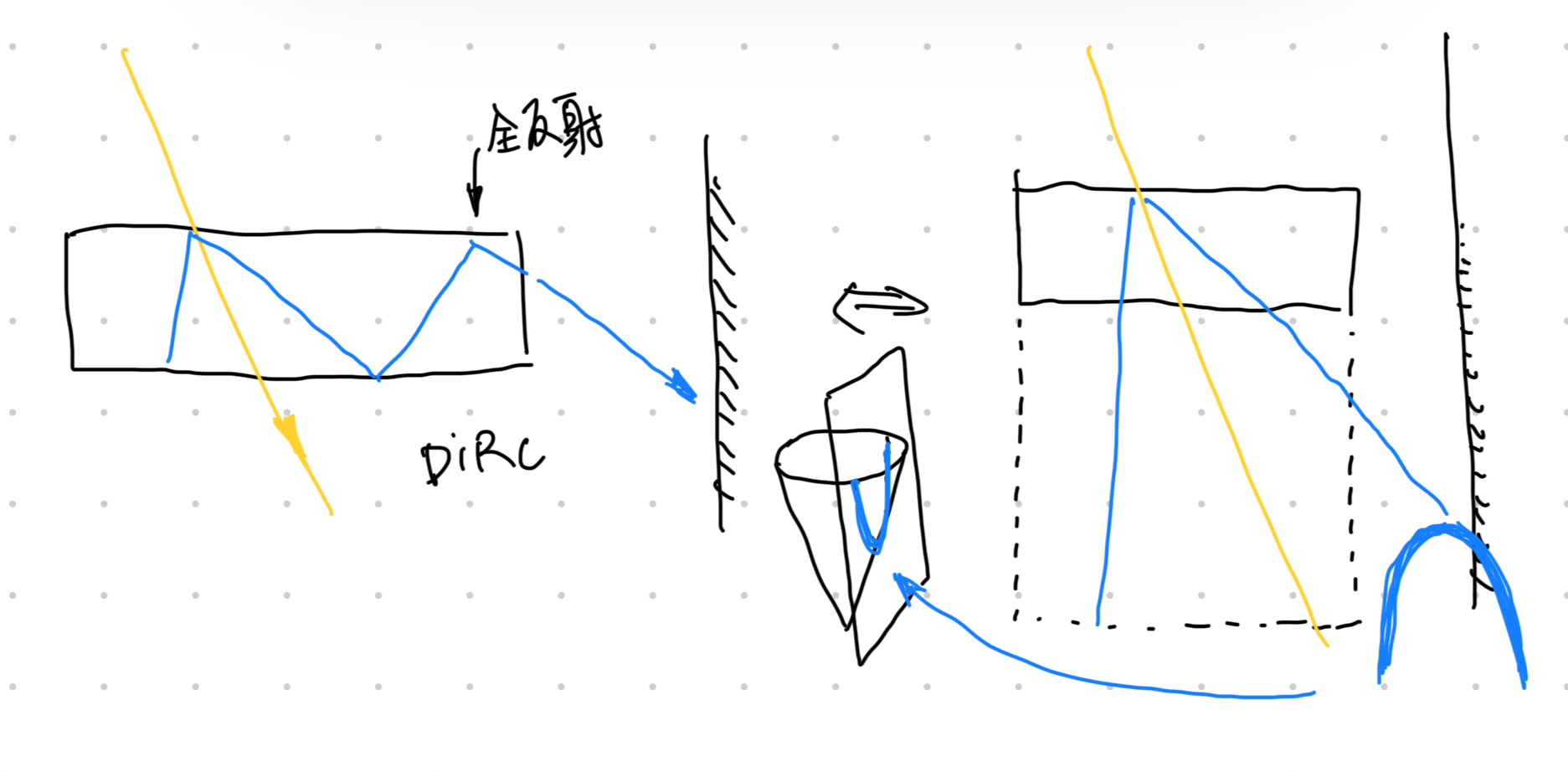
/_img/particle-detector/DIRC.jpg

有点类似于 RICH, 解决了 RICH 需要放大小角度 (Cherenkov 角) 需要很长距离的问题

时间型

CCT

通过测量到达时间来确定 Cherenkov 角

TOP

通过同时测量切伦科夫传播时间和出射位置鉴别粒子
(有点类似于 CCT + DIRC)

穿越辐射探测器

信噪比: $\frac{S}{I_{\mathrm{bg}}} ∼ \frac{1}{Z^{3.5}}$ (选择 $Z$ 大的)
穿越辐射特点
- 辐射产额低, 需要使用多层辐射体
- 辐射角小, 所以一般测量得到的是电离能损信号和穿越辐射信号的叠加
- 一般用于鉴别高能粒子
- 一般不能给出精确的 $γ$
可以用 $γ$ 阈值来对粒子进行分辨

大型谱仪

谱仪的要求
- 大接受度
- 能对粒子进行精确测量
- 能鉴别粒子种类
- 能探测多粒子事例
- 相应速度快
- 排除本底能力强
- 寿命长
粒子以及相关测量
- TOF 可以测量速度 $β$
- Cherenkov 可以测量速度 $β$ , 同时也可以鉴别是否为带电粒子 (甄别 $γ$ , 中子)
- 穿越辐射, 对于极端相对论粒子
- 量能器 (电磁, 强子) 可以用于电子 - 强子鉴别
- $μ$ 子, 一般放在探测器最后, 用对带电粒子敏感的探测器
- 径迹测量 + 磁场可以测量动量 (顶点测量)
- …

设计目标与测量误差

设计的时候会有一个测量要求, 比如动量分辨好于多少, 能够分辨什么什么粒子能量
测量的时候会有另一个叫作两个事例的区分能力, 有点不太一样, 是 $σ$ 还是 $2 σ$

其他

主要是一些前面的知识的回看以及一些整理:

宇宙线: (海平面) 一个指甲每秒一个 ( $1 \mathrm{count} ⋅ \mathrm{cm}^{-2} ⋅ \mathrm{s}^{-1}$ )
宇宙线对静电计的放电
- 宇宙线 (海平面) $2.74 \mathrm{pair} ⋅ \mathrm{cm}^{-3} ⋅ \mathrm{s}^{-1}$
- 对 $50 \mathrm{cm}^3$ 的静电计的电离放电电流: $2.74 × 50 × 1.6 × 10^{-19} \mathrm{A}$
电离能损的粒子鉴别: MIP (最小电离粒子) 在 $β γ = 3 ∼ 4$
为什么能做 PID (粒子鉴别)?
- 电离能损 $\mathrm{d} E / \mathrm{d} x$ 是一个 $β γ$ 的函数, 与粒子无关
- 相同动量但是不同质量的粒子 $β γ$ 不同, 沉积能量不同
一些关于一般 PID 的想法
其实别说用的探测器有多么先进, 只靠一个是不可能确定粒子种类是什么的. (倒也不是说理论上不行, 或者理论有问题之类的东西)
而是假如只测量一个能量 (能损), 那么怎么可能知道粒子是什么呢. 还得是联合测量, 只不过某些探测器可以同时做到测到各种不同的参量, 所以可以符合匹配而已.

emm… 看来最后大家都是在做一个参量设计和参量提取的事情.
韧致辐射:
- 和介质关系: 韧致辐射增幅 $A \propto a$ (加速度 $\propto Z / m$ ), 所以最终辐射强度 $\propto Z^2 / m^2$
- 和入射粒子 $\propto$ 能量, $\propto 1/m^2$ (对电子一般不可忽略, 见 Corsika Physics)
- 临界能量 (和电离能损相同, 或是 $(\mathrm{d} E / \mathrm{d} X)_{\mathrm{ion}} = (Δ E)_{\mathrm{brem}} / X_0$ )
  电子的临界能量 $\propto 1/Z^{2}$
  因为电子的电离能损近似一条直线 (常数), 所以临界能量与 $X_{0}$ 成正比.
- 辐射长度 (混合物 $\frac{1}{X_0} = ∑ \frac{w_i}{X_i}$ ) $E = E_0 \mathrm{e}^{- x / X_0}$
- 射程 $R(E) = ∫_E^0 \frac{\mathrm{d} E}{\mathrm{d} E / \mathrm{d} x}$
  用来估计屏蔽/吸收的射程
  入射一般是个谱 (宇宙线), 射程可以变成一个阈值.

关于光的相互作用形式

说起来这个, 一同学高能所面试还被问到了这个…

光生电子对
光核作用
光电效应
- 光电子发射有角分布 (结合能, 原子反冲)
康普顿散射 (逆康普顿)
- 散射光子 $E_{γ}' = \frac{E_{γ}}{1 + \frac{E_{γ}}{m_e c^2 (1 - cos θ)}}$
  反冲电子 $E_e = \frac{E_{γ}}{1 + \frac{m_e c^2}{E_{γ} (1 - cos θ)}}$
- 截面 $σ \propto Z$
- 康普顿沿: 单能入射光子产生的电子反冲能谱有一个平台 (康普顿平台) (最大反冲能量处有一个尖锐边缘, 康普顿沿)
  以及闪烁体探测器的康普顿沿 (为什么? 因为不是单能的)
  
  利用康普顿沿来计算入射光子能量
  $E_{γ} = \frac{1}{2} (E_{e, \mathrm{max}} + \sqrt{E_{e, \mathrm{max}}^2 + 2 c^2 E_{e, \mathrm{max}} m_e})$
光衰减系数 $I = I_0 \mathrm{e}^{-μ x}$
- 衰减长度 $≠$ 射程 (光没有)
- 光和粒子过介质后的不同 (计数上)
切伦科夫辐射
穿越辐射
中子

能量低能热中子慢中子/中能中子快中子

探测方法中子衍射核反应, 核裂变, 核活化核反冲
簇射体
- 电磁簇射 Pb (光子 - 正负电子对 (光生电子对) - 光子 (韧致辐射), Z 大)
- 强子簇射 Cu, Fe

能量	低能	热中子	慢中子/中能中子	快中子
探测方法	中子衍射	核反应, 核裂变, 核活化		核反冲

物理图像

什么是物理图像?

后记

概念题真是要人老命.

(我们应当像计算机一样引入 context 的概念, 并引入外部图数据库 Knowledge Graph Database 进行辅助说明, 以此解决该死的概念爆炸的问题)