About

要背的公式

矢量分析公式
Maxwell 方程
\[\left\{\begin{matrix} ∇ × \boldsymbol{E} & = & - \frac{∂ \boldsymbol{B}}{∂ t}\\∇ × \boldsymbol{H} & = & \frac{∂ \boldsymbol{D}}{∂ t} + \boldsymbol{J}\\ ∇ ⋅ \boldsymbol{D} & = & ρ\\∇ ⋅ \boldsymbol{B} & = & 0\end{matrix}\right.\]

边值关系

\[\left\{\begin{matrix} \boldsymbol{e}_n × (\boldsymbol{E}_2 - \boldsymbol{E}_1) & = & 0 \\ \boldsymbol{e}_n × (\boldsymbol{H}_2 - \boldsymbol{H}_1) & = & α \\ \boldsymbol{e}_n ⋅ (\boldsymbol{D}_2 - \boldsymbol{D}_1) & = & σ \\ \boldsymbol{e}_n ⋅ (\boldsymbol{B}_2 - \boldsymbol{B}_1) & = & 0 \end{matrix}\right.\]
d'Alembert 方程
\[\begin{matrix} ∇^2 \boldsymbol{A} - \frac{1}{c^2} ∂_t^2 \boldsymbol{A} & = & - μ_0 \boldsymbol{J} \\ ∇^2 \varphi - \frac{1}{c^2} ∂_t^2 \varphi & = & 0 \end{matrix} \qquad ∇ ⋅ \boldsymbol{A} + \frac{1}{c^2} ∂_t \varphi = 0\]
散射折射系数
- \(\boldsymbol{E}_{\bot}\) 垂直分量
  \[R = \frac{E'}{E} = \frac{\sqrt{ε_1} cos θ - \sqrt{ε_2} cos θ”}{\sqrt{ε_1} cos θ + \sqrt{ε_2} cos θ”} = - \frac{sin (θ - θ”)}{sin (θ + θ”)}\]
  
  \[T = \frac{E”}{E} = \frac{2 \sqrt{ε_1} cos θ}{\sqrt{ε_1} cos θ + \sqrt{ε_2} cos θ”} = \frac{2 cos θ sin θ”}{sin(θ + θ”)}\]
- \(\boldsymbol{E}_{\parallel}\) 平行分量
  \[R = \frac{E'}{E} = \frac{tan(θ - θ”)}{tan(θ + θ”)}\]
  
  \[T = \frac{E”}{E} = \frac{2 cos θ sin θ”}{sin(θ + θ”) cos(θ - θ”)}\]
- 全反射 \(sin θ > n_{21}\)
  透入深度 \(κ^{-1} = \frac{1}{k \sqrt{sin^2 θ - n_{21}^2}}\)
  
  导体的透入深度 \(δ = \frac{1}{α} = \sqrt{\frac{2}{ω μ σ}}\)
谐振腔 \(\frac{n π}{L}\)
波导, 波模截止频率 \(ω = \frac{π}{\sqrt{μ ε}} \sqrt{(\frac{m}{a})^2 + (\frac{n}{b})^2}\)
电偶极辐射
- 电偶极子 \(\boldsymbol{p} = q \boldsymbol{l}\), 磁偶极子 \(\boldsymbol{m} = \frac{1}{2} \boldsymbol{r} × \boldsymbol{p}\) (或者 \(\boldsymbol{m} = i \boldsymbol{s}\))
- 电偶极辐射: \(\boldsymbol{A} = \frac{μ_0 e^{i k r}}{4 π r} \dot{\boldsymbol{p}}\)
- 磁偶极辐射: \(\boldsymbol{A} = \frac{i k μ_0 e^{i k r}}{4 π r} \boldsymbol{e}_r × \boldsymbol{m}\)
- 计算的技巧: \(∇ = i k \boldsymbol{e}_r, ∂_t = - i ω\) (近似结果)
  \(\boldsymbol{E} = \frac{i c}{k} ∇ × \boldsymbol{B}, \boldsymbol{B} = ∇ × \boldsymbol{A}, \boldsymbol{S} = \frac{1}{2} \mathrm{Re}(\boldsymbol{E}^{*} × \boldsymbol{H})\)
四维量
- \(\boldsymbol{r} = (c t, \boldsymbol{r}_3)\), \(\boldsymbol{v} = \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} τ} = γ (c, \boldsymbol{v}_3)\)
  速度变换: \(u_x' = \frac{u_x - v}{1 - \frac{v u_x}{c^2}}, u_y' = \frac{u_y}{γ(1 - \frac{v u_y}{c^2})}\).
- \(\boldsymbol{p} = γ (\frac{W}{c}, \boldsymbol{p}_3)\), \(\boldsymbol{F} = m_0 γ (\frac{\mathrm{d} γ}{\mathrm{d} t} c, (\frac{\mathrm{d} γ}{\mathrm{d} t} \boldsymbol{u}_3 + γ \boldsymbol{a}_3))\)
- \(\boldsymbol{j} = (ρ c, \boldsymbol{j}_3)\), \(\boldsymbol{A} = (\frac{φ}{c}, \boldsymbol{A}_3)\), \(F^{μ\nu} = ∂^{μ} A^{ν} - ∂^{ν} A^{μ} = \left( \begin{matrix} 0 & - \frac{E_1}{c} & - \frac{E_2}{c} & - \frac{E_3}{c} \\ \frac{E_1}{c} & 0 & - B_3 & B_2 \\ \frac{E_2}{c} & B_3 & 0 & - B_1 \\ \frac{E_3}{c} & - B_2 & B_1 & 0 \end{matrix} \right)\).
- Lorentz 变换矩阵 \(Λ = \left( \begin{matrix} γ & - γ β & 0 & 0 \\ - β γ & γ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right)\)

电磁波的传播

电磁波方程

(真空) 电磁波方程的导出
\[\left\{\begin{matrix} ∇ × \boldsymbol{E} & = & - \frac{∂ \boldsymbol{B}}{∂ t}\\∇ × \boldsymbol{H} & = & \frac{∂ \boldsymbol{D}}{∂ t} + \boldsymbol{J}\\ ∇ ⋅ \boldsymbol{D} & = & ρ\\∇ ⋅ \boldsymbol{B} & = & 0\end{matrix}\right.\]

核心的一个变换就是 \(∇ × (∇ × \boldsymbol{E}) = - \frac{∂}{∂ t} ∇ × \boldsymbol{B}\). 最终的一个结果:

\[\begin{matrix} ∇^2 \boldsymbol{E} - \frac{1}{c^2} \frac{∂^2}{∂ t^2} \boldsymbol{E} & = & 0\\ ∇^2 \boldsymbol{B} - \frac{1}{c^2} \frac{∂^2}{∂ t^2} \boldsymbol{B} & = & 0\end{matrix}\]

有介质的情况: \(\boldsymbol{D}(ω) = ε(ω) \boldsymbol{E}(ω), \boldsymbol{B}(ω) = μ(ω) \boldsymbol{H}(ω)\).
平面电磁波
\[\boldsymbol{E} = \boldsymbol{E}_0 e^{i (\boldsymbol{k} ⋅ \boldsymbol{x} - ω t)}, \boldsymbol{B} = \sqrt{μ ε} \boldsymbol{e}_k × \boldsymbol{E}\]
能量密度 \(w = \frac{1}{2} (\boldsymbol{E} ⋅ \boldsymbol{D} + \boldsymbol{H} ⋅ \boldsymbol{B})\),
线性介质中: \(w = \frac{1}{2}(ε \boldsymbol{E}^2 + \frac{1}{μ} \boldsymbol{B}^2)\), 平面电磁波中: \(w = ε E^2 = \frac{1}{μ} B^2\).

一些别的说明

若 \(\left(\begin{matrix} \boldsymbol{E} \\ \boldsymbol{D} \\ \boldsymbol{B} \\ \boldsymbol{H} \end{matrix}\right) = \left(\begin{matrix} \boldsymbol{E}_0 \\ \boldsymbol{D}_0 \\ \boldsymbol{B}_0 \\ \boldsymbol{H}_0 \end{matrix}\right) e^{i (\boldsymbol{k} ⋅ \boldsymbol{x} - ω t)}\), 那么有结论:

平均值 \(\bar{w} = \frac{1}{2} ε E_0^2 = \frac{1}{2 μ} B_0^2\)
能流密度 \(\boldsymbol{S} = \boldsymbol{E} × \boldsymbol{H}\)
平面电磁波中 \(\boldsymbol{S} = \sqrt{\frac{ε}{μ}} E^2 \boldsymbol{e}_k = \frac{1}{\sqrt{μ ε}} w \boldsymbol{e}_k = v w \boldsymbol{e}_k\).

平均值 \(\bar{\boldsymbol{S}} = \frac{1}{2} \mathrm{Re} (\boldsymbol{E}^{*} × \boldsymbol{H}) = \frac{1}{2} \sqrt{\frac{ε}{μ}} E_0^2 \boldsymbol{e}_k\)

习题

平面波合成 \(\boldsymbol{E} = \boldsymbol{E}_1 e^{\varphi_1} + \boldsymbol{E}_2 e^{\varphi_2}\)
必要的时候可以考虑用 \(e^{i \varphi} = cos \varphi + i sin \varphi\) 以及三角函数进行展开化简.
波的相关知识
- 波的相位传播速度 (波速) \(v_p = \frac{ω}{k} = \frac{∂ x}{∂ t} = \frac{\mathrm{d} E / \mathrm{d}t}{\mathrm{d} E / \mathrm{d}x}\)
- 波的群速度 \(v_g = \frac{\mathrm{d} ω}{\mathrm{d} k}\)

介质面

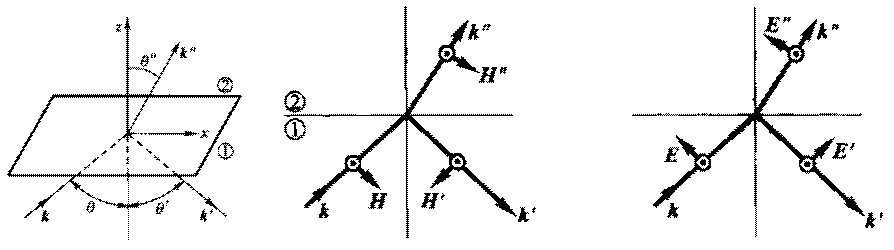
/_img/pieces/fresnel.png

反射波矢 \(θ' = θ\)
折射波矢 \(\frac{sin θ}{sin θ”} = \frac{\sqrt{μ_2 ε_2}}{\sqrt{μ_1 ε_1}} = n_{21}\)
偏振
- \(\boldsymbol{E} \bot\) 入射面
  - 反射 \(R = \frac{E'}{E} = \frac{\sqrt{ε_1} cos θ - \sqrt{ε_2} cos θ”}{\sqrt{ε_1} cos θ + \sqrt{ε_2} cos θ”} = - \frac{sin (θ - θ”)}{sin (θ + θ”)}\)
  - 折射 \(T = \frac{E”}{E} = \frac{2 \sqrt{ε_1} cos θ}{\sqrt{ε_1} cos θ + \sqrt{ε_2} cos θ”} = \frac{2 cos θ sin θ”}{sin(θ + θ”)}\)
- \(\boldsymbol{E} \parallel\) 入射面
  - 反射 \(R = \frac{E'}{E} = \frac{tan(θ - θ”)}{tan(θ + θ”)}\)
  - 折射 \(T = \frac{E”}{E} = \frac{2 cos θ sin θ”}{sin(θ + θ”) cos(θ - θ”)}\)
全反射 \(sin θ > n_{21}\)
此时 \(k_x” = i k \sqrt{sin^2 θ - n_{21}^2} = i κ\), 折射波电场为 \(\boldsymbol{E}” = \boldsymbol{E}_0” e^{- κ x} e^{i (k x - ω t)}\) (隐失波).

习题

计算折射和反射系数
1. 分解电场强度为 \(\bot\) 和 \(\parallel\) 分量
2. 分别计算 \(R_{\bot}\), \(R_{\parallel}\) 等的值
3. 合并计算 \(E'\) 得到 \(R\) 和 \(T\)
全反射
- 全反射条件 \(sin θ > n_{21}\)
- 透入深度 \(κ^{-1} = \frac{1}{k \sqrt{sin^2 θ - n_{21}^2}}\)

导体

导体中的平面波解 \(\boldsymbol{E}(\boldsymbol{r}) = \boldsymbol{E}_0 e^{i \boldsymbol{k} ⋅ \boldsymbol{x}}, \boldsymbol{k} = \boldsymbol{β} + i \boldsymbol{α}\), 其中 \(β^2 - α^2 = ω^2 μ ε, \boldsymbol{α} ⋅ \boldsymbol{β} = \frac{1}{2} ω μ σ\).

推导证明

在导体中, \(\boldsymbol{J} = σ \boldsymbol{E}\), 于是 \(∇ × \boldsymbol{H} = - \frac{∂}{∂ t} \boldsymbol{D} + σ \boldsymbol{E}\).
假设有 \(\boldsymbol{D} = ε \boldsymbol{E} = ε \boldsymbol{E}_0 e^{i ω t}\), 于是代入上面的结果应当可以得到有复电容率: \(ε' = ε + i \frac{σ}{ω}\), \(∇ × \boldsymbol{H} = - i ω ε' \boldsymbol{E}\), 于是和正常平面波类似推导.
在一定频率下有 Helmholtz 方程: \(∇^2 \boldsymbol{E} + ω^2 μ ε' \boldsymbol{E} = 0\).

在垂直入射的情况下: \(\boldsymbol{α} ⋅ \boldsymbol{β} = α β\), 那么这个时候可以解得 \(α, β\).

良导体的趋肤深度
在良导体中: \(k^2 ≈ i ω μ σ\), 于是得到 \(α ≈ β ≈ \sqrt{\frac{ω μ σ}{2}}\). 穿透深度 \(δ = \frac{1}{α} = \sqrt{\frac{2}{ω μ σ}}\) (\(α\) 为衰减项).

并且主要其作用的是磁场 \(\sqrt{\frac{μ}{ε}} \frac{H}{E} = \sqrt{\frac{σ}{ω ε}} \gg 1\).
反射
\[R = \frac{(1 - \sqrt{\frac{2 ω ε_0}{σ}})^2 + 1}{(1 + \sqrt{\frac{2 ω ε_0}{σ}})^2 + 1} ≈ 1 - 2 \sqrt{\frac{2 ω ε_0}{σ}}\]

在理想导体情况或者是 \(ω\) 较小 (波长较长), 可以近似认为反射系数接近 1 (全反射).

习题

表面电阻计算

谐振腔和波导

理想边界条件
对于理想的导体问题, 应有 \(\boldsymbol{E}_1 = \boldsymbol{H}_1 = 0\) (导体内部没有场)

\[\begin{matrix} \boldsymbol{e}_n × \boldsymbol{E} & = & 0 \\ \boldsymbol{e}_n × \boldsymbol{H} & = & \boldsymbol{α} \\ \boldsymbol{e}_n ⋅ \boldsymbol{D} & = & σ \\ \boldsymbol{e}_n ⋅ \boldsymbol{B} & = & 0 \end{matrix}\]

其中 \(\boldsymbol{E}, \boldsymbol{H}, \boldsymbol{D}, \boldsymbol{B}\) 为介质侧的场, 即导体表面上, 电场线和界面垂直, 磁感应线和界面向切.

(该性质可以导出无穷大导体间只能传播一种偏振平面波)
谐振腔
\[∇^2 u + k^2 u = 0\]

在有限立方体 \(L_1 × L_2 × L_3\) 内有驻波解 (边界条件 \(E_x = 0, \frac{∂ E_x}{∂ x} = 0, (x = 0, L_1)\) 的自然结果).

结果 \(k_x^2 + k_y^2 + k_z^2 = ω^2 μ ε\), \(k_x = \frac{m π}{L_1}, k_y = \frac{n π}{L_2}, k_z = \frac{p π}{L_3}\). (并且 \(∇ ⋅ \boldsymbol{E} = 0 ⇒ k_x A_1 + k_y A_2 + k_z A_3 = 0\) 非独立)
波导
在 \(L_3\) 方向上不做限制, 仅在 \(L_1, L_2\) 方向上有边界条件.
推导证明
- 边界条件 \(E_x = E_y = 0, \frac{∂ E_x}{∂ x} = 0, (x = 0, a)\), \(E_x = E_z = 0, \frac{∂ E_y}{∂ y} = 0, (y = 0, b)\).
- 最终结果
  \[\left\{\begin{matrix} E_x & = & A_1 cos k_x x sin k_y y e^{i k_z z} \\ E_y & = & A_2 sin k_x x cos k_y y e^{i k_z z} \\ E_z & = & A_3 sin k_x x sin k_y y e^{i k_z z} \end{matrix}\right.\]
  
  其中在 \(x, y\) 方向上有驻波条件 \(k_x = \frac{m π}{a}, k_y = \frac{n π}{b} (m, n = 0, 1, 2, …)\).
- 波模
  波进行一个分解为两个 \(E_z = 0\) TE 波 (横电波), \(H_z = 0\) TM 波 (横磁波) 于是分别可以通过 \((m, n)\) 来确定, 称为波模.
- 截止频率
  能够在波导内传播的波的最低频率 \(ω_c\) 称为波模的截止频率:
  
  \[ω_{c, m, n} = \frac{π}{\sqrt{μ ε}} \sqrt{(\frac{m}{a})^2 + (\frac{n}{b})^2}\]
  更多的解释
  - 截止频率的一个来源: 因为 \(k^2 = k_x^2 + k_y^2 + k_z^2\), 若使得 \(k_z\) 成为虚数, 则波为衰减波, 即无法在波导内传播.
  - 对于 \(TE_{10}\) 波, 最低截止频率 \(\frac{1}{2 π} ω_{c,1,0} = \frac{1}{2 a \sqrt{μ ε}}\), 截止波长 \(λ_{c,1,0} = 2 a\).
    (限制了波导的应用波段为厘米波段)
  - \(TE_{10}\) 电流分布

习题

电磁波的辐射

矢势和标势

在电磁场中使用 \(\varphi, \boldsymbol{A}\) 来描述电磁场的势: \(\boldsymbol{B} = ∇ × \boldsymbol{A}, \boldsymbol{E} = - ∇ \varphi - \frac{∂ \boldsymbol{A}}{∂ t}\).

一些小说明

可以将场分解为无旋场和无散场, 于是电场的无旋部分会和库仑场对应.

\(\varphi, \boldsymbol{A}\) 满足规范变换不变性:

\[\begin{matrix} \boldsymbol{A} & → & \boldsymbol{A}' & = & \boldsymbol{A} + ∇ ψ \\ \varphi & → & \varphi' & = & \varphi - \frac{∂ ψ}{∂ t} \end{matrix}\]

其中 \(ψ\) 为任意 (时空) 函数. 一般希望将最终的结果变换为:

库仑规范
\[\begin{matrix} ∇^2 \boldsymbol{A} - \frac{1}{c^2} \frac{∂^2 \boldsymbol{A}}{∂ t^2} - \frac{1}{c^2} \frac{∂}{∂ t} ∇ \varphi = - μ_0 \boldsymbol{J} \\ ∇^2 \varphi = - \frac{ρ}{ε_0} \end{matrix} \qquad (∇ ⋅ \boldsymbol{A} = 0)\]
洛仑兹规范 \(∇ ⋅ \boldsymbol{A} + \frac{1}{c^2} \frac{∂ \varphi}{∂ t} = 0\)
\[\begin{matrix} ∇^2 \boldsymbol{A} - \frac{1}{c^2} \frac{∂^2 \boldsymbol{A}}{∂ t^2} = - μ_0 \boldsymbol{J}\\ ∇^2 \varphi - \frac{1}{c^2} \frac{∂^2 \varphi}{∂ t^2} = - \frac{ρ}{ε_0} \end{matrix} \qquad (∇ ⋅ \boldsymbol{A} + \frac{1}{c^2} \frac{∂ \varphi}{∂ t} = 0)\]

习题

平面电磁波的势
\[\boldsymbol{A} = \boldsymbol{A}_0 e^{i (\boldsymbol{k} ⋅ \boldsymbol{x} - ω t)}, \varphi = \varphi_0 e^{i (\boldsymbol{k} ⋅ \boldsymbol{x} - ω t)}\]

于是可以用来表示磁场和电场:

\[\boldsymbol{B} = ∇ × \boldsymbol{A} = i \boldsymbol{k} × \boldsymbol{A}, \boldsymbol{E} = - ∇ \varphi - \frac{∂ \boldsymbol{A}}{∂ t} = - ∇ \varphi - i ω \boldsymbol{A}\]

并且还可以将矢势复数展开 \(\boldsymbol{A} = ∑ a_j e^{i \boldsymbol{k}_j ⋅ \boldsymbol{x}} + a^{*}_j e^{i \boldsymbol{k}_j ⋅ \boldsymbol{x}}\).

推迟势

\[\begin{matrix} \varphi(\boldsymbol{r}, t) = ∫_V \frac{ρ(\boldsymbol{r}', t - \frac{| \boldsymbol{r} - \boldsymbol{r}' |}{c})}{4 π ε_0 | \boldsymbol{r} - \boldsymbol{r}' |} \mathrm{d}V' \\ \boldsymbol{A}(\boldsymbol{r}, t) = \frac{μ_0}{4 π} ∫_V \frac{\boldsymbol{J}(\boldsymbol{r}', t - \frac{| \boldsymbol{r} - \boldsymbol{r}' |}{c})}{| \boldsymbol{r} - \boldsymbol{r}' |} \mathrm{d}V' \end{matrix}\]

证明推导和习题

上解为达朗贝尔方程 (洛仑兹规范得到) 的自然结果:

\[∇^2 \varphi - \frac{1}{c^2} \frac{∂^2 \varphi}{∂ t^2} = - \frac{ρ}{ε_0}\]

使用冲量定理来拆解方程, 然后代入达朗贝尔公式去求解.

推迟势满足洛仑兹条件.

电偶极辐射, 磁偶极辐射, 电四极辐射

对于 \(\boldsymbol{J}(\boldsymbol{r}', t - \frac{| \boldsymbol{r} - \boldsymbol{r}' |}{| \boldsymbol{r} - \boldsymbol{r}' |}) = \boldsymbol{J} e^{i (\boldsymbol{k} ⋅ \boldsymbol{r} - ω t)}\) 进行矢势展开

\[\boldsymbol{A}(\boldsymbol{r}) = \frac{μ_0 e^{i \boldsymbol{k} \boldsymbol{r}}}{4 π r} ∫_V \boldsymbol{J}(\boldsymbol{r}') (1 - i \boldsymbol{k} \boldsymbol{e}_r ⋅ \boldsymbol{x}' + …) \mathrm{d}V'\]

展开区域的一个说明

近区 \(r \ll λ\)
感应区 \(r ∼ λ\)
远区 (辐射区) \(r \gg λ\)

电偶极辐射 \(\frac{μ_0 e^{i \boldsymbol{k} \boldsymbol{r}}}{4 π r} ∫_V \boldsymbol{J}(\boldsymbol{r}') \mathrm{d}V'\)
\[\begin{matrix} \boldsymbol{A}(\boldsymbol{r}) = \frac{μ_0 e^{i \boldsymbol{k} ⋅ \boldsymbol{r}}}{4 π r} \dot{\boldsymbol{p}} \\ \boldsymbol{B} = \frac{1}{4 π ε_0 c^3 r} e^{i \boldsymbol{k} ⋅ \boldsymbol{r}} \ddot{\boldsymbol{p}} × \boldsymbol{e}_r \\ \boldsymbol{E} = \frac{e^{i \boldsymbol{k} ⋅ \boldsymbol{r}}}{4 π ε_0 c^2 r} (\ddot{\boldsymbol{p}} × \boldsymbol{e}_r) × \boldsymbol{e}_r \end{matrix}\]
更加详细的解释

方程的一个证明:
- \(∫_V \boldsymbol{J}(\boldsymbol{r}') \mathrm{d}V' = ∑ q \boldsymbol{v} = ∑ q \dot{\boldsymbol{x}} = \dot{\boldsymbol{p}}\), 也就是为什么说是电偶极辐射, 于是得到 \(\boldsymbol{A} = \frac{μ_0 e^{i k r}}{4 π r} \dot{\boldsymbol{p}}\).
- 计算 \(\boldsymbol{B} = ∇ × \boldsymbol{A}, \boldsymbol{E} = \frac{i c}{k} ∇ × \boldsymbol{B}\) 的时候, 对算子 \(∇\) 做一个近似: 保留 \(\frac{1}{r}\) (因为是远场近似), 于是 \(∇ → i k \boldsymbol{e}_r, \frac{∂}{∂ t} → - i ω\).
- \(\boldsymbol{B} = ∇ × \boldsymbol{A}, \boldsymbol{E} = \frac{i c}{k} ∇ × \boldsymbol{B}\)
辐射的能量关系:
- \(\boldsymbol{S} = \frac{1}{2} \mathrm{Re}(\boldsymbol{E}^{*} × \boldsymbol{H}) = \frac{|\ddot{\boldsymbol{p}}|^2}{32 π^2 ε_0 c^3 r^2} sin^2 θ \boldsymbol{e}_r\)
- \(P = \oint | \boldsymbol{S} | r^2 \mathrm{d}Ω = \frac{1}{4 π ε_0} \frac{| \ddot{\boldsymbol{p}} |^2}{3 c^3}\)
四极子辐射 \(\frac{- k μ_0 e^{i k r}}{4 π r} ∫_V \boldsymbol{J}(\boldsymbol{r}') (\boldsymbol{e}_r ⋅ \boldsymbol{r}') \mathrm{d}V'\)

习题和结论

电荷质量相同的粒子相向运动不会 产生电偶极辐射和磁偶极辐射
电偶极辐射因为相向运动在质心系下没有电偶极子 (速度为零) 所以不产生:

\[\dot{\boldsymbol{p}} = q \dot{x}_1 + q \dot{x}_2 = 0 ⇒ \boldsymbol{A} = \frac{μ_0 e^{i k r}}{4 π r} \dot{\boldsymbol{p}} = 0\]

磁偶极子辐射因为径向运动没有磁矩所以不产生:

\[\boldsymbol{m} = \frac{1}{2} (\boldsymbol{x}_1 × q \dot{\boldsymbol{x}}_2 + \boldsymbol{x}_2 × q \dot{\boldsymbol{x}}_2) = 0 ⇒ \boldsymbol{A} = \frac{i k μ e^{i k r}}{4 π r} \boldsymbol{e}_r × \boldsymbol{m} = 0\]

可以利用结论来快速判断是否产生电偶极辐射, 比如球对称电荷分布径向运动就不会有辐射.

(又: 稳恒的条件是绝对不会有辐射的就是了.)
计算偶极辐射和四极子辐射, 以及场和能流
1. 计算 \(\boldsymbol{p}\) 或者 \(\boldsymbol{m}\)
2. 代入公式 \(\boldsymbol{A} = \frac{μ_0 e^{i k r}}{4 π r} \dot{\boldsymbol{p}}\) 或者 \(\boldsymbol{A} = \frac{i k μ_0 e^{i k r}}{4 π r} \boldsymbol{e}_r × \boldsymbol{m}\).
  一般会换成球坐标系会比较方便计算, 变换关系如下:
  
  \[\left( \begin{matrix} \boldsymbol{e}_x \\ \boldsymbol{e}_y \\ \boldsymbol{e}_z \end{matrix} \right) = \left( \begin{matrix} sin θ cos φ & cos θ cos φ & - sin φ \\ sin θ sin φ & cos θ sin φ & cos φ \\ cos θ & - sin θ & 0 \end{matrix} \right) \left( \begin{matrix} e_r \\ e_{θ} \\ e_{φ} \end{matrix} \right)\]
  
  以及球坐标里面的一些计算结果:
  
  \[e_i × e_j = ε_{ijk} e_k,\quad ε_{ijk} = 1\ \mathrm{iff}\ (i, j, k) = (ρ, θ, φ)\]
3. 计算磁场和电场 \(\boldsymbol{B} = ∇ × \boldsymbol{A} = i k \boldsymbol{e}_r × \boldsymbol{A}\), \(\boldsymbol{E} = \frac{i c}{k} ∇ × \boldsymbol{B} = c \boldsymbol{B} × \boldsymbol{e}_r\), \(\boldsymbol{S} = \frac{c}{2 μ_0} (\boldsymbol{B}^{*} ⋅ \boldsymbol{B}) \boldsymbol{e}_r\).
  常用结论:
  - 电偶极辐射场:
    \[\begin{matrix} \boldsymbol{A} & = & \frac{μ_0 e^{i k r}}{4 π r} \dot{\boldsymbol{p}} \\ \boldsymbol{B} & = & i k \boldsymbol{e}_r × \boldsymbol{A} = \frac{e^{i k r}}{4 π ε_0 c^3 r} \ddot{\boldsymbol{p}} × \boldsymbol{e}_r \\ \boldsymbol{E} & = & c \boldsymbol{B} × \boldsymbol{e}_r = \frac{e^{i k r}}{4 π ε_0 c^2 r} (\ddot{\boldsymbol{p}} × \boldsymbol{e}_r) × \boldsymbol{e}_r \end{matrix}\]
  - 磁偶极辐射场:
    \[\begin{matrix} \boldsymbol{A} & = & \frac{i k μ_0 e^{i k r}}{4 π r} \boldsymbol{e}_r × \boldsymbol{m} \\ \boldsymbol{B} & = & i k \boldsymbol{e}_r × \boldsymbol{A} = \frac{μ_0 e^{i k r}}{4 π c^2 r} (\ddot{\boldsymbol{m}} × \boldsymbol{e}_r) × \boldsymbol{e}_r \\ \boldsymbol{E} & = & c \boldsymbol{B} × \boldsymbol{e}_r = \frac{μ_0 e^{i k r}}{4 π c r} \ddot{\boldsymbol{m}} × \boldsymbol{e}_r \end{matrix}\]

电磁波衍射

Kirchhoff 公式:

\[\begin{matrix} ψ(\boldsymbol{r}) & = & - \frac{1}{4 π} \oint_s [ψ(\boldsymbol{r}') ∇' \frac{e^{i k r}}{r} - \frac{e^{i k r}}{r} ∇' ψ(\boldsymbol{r}')] ⋅ \mathrm{d}\boldsymbol{S}' \\ & = & - \frac{1}{4 π} \oint_S \frac{e^{i k r}}{r} \boldsymbol{e}_n ⋅ [∇' ψ + (i k - \frac{1}{r}) \frac{\boldsymbol{r}}{r} ψ] \mathrm{d}S'\end{matrix}\]

证明推导

电磁场动量

动量密度:
\[g = ε_0 \boldsymbol{E} × \boldsymbol{B} = μ_0 ε_0 \boldsymbol{E} × \boldsymbol{H} = \frac{1}{c^2} \boldsymbol{S}\]
动量流密度
\[\mathcal{J} = - ε_0 \boldsymbol{E} \boldsymbol{E} - \frac{1}{μ_0} \boldsymbol{B} \boldsymbol{B} + \frac{1}{2} \mathcal{J} (ε_0 E^2 + \frac{1}{μ_0} B^2)\]

详细说明

电磁场力 \(\boldsymbol{f} = ρ \boldsymbol{E} + \boldsymbol{J} × \boldsymbol{B}\)
换掉 \(ρ = ε_0 ∇ ⋅ \boldsymbol{E}, \boldsymbol{J} = \frac{1}{μ_0} ∇ × \boldsymbol{B} - ε_0 \frac{∂ \boldsymbol{E}}{∂ t}\), 得到 \(\boldsymbol{f} = [ε_0 (∇ ⋅ \boldsymbol{E}) \boldsymbol{E} + \frac{1}{μ_0} (∇ ⋅ \boldsymbol{B}) \boldsymbol{B} + \frac{1}{μ_0} (∇ × \boldsymbol{B}) × \boldsymbol{B} + ε_0 (∇ × \boldsymbol{E}) × \boldsymbol{E}] - ε_0 \frac{∂}{∂ t} (\boldsymbol{E} × \boldsymbol{B})\).
其中通过变形可以得到 \(\boldsymbol{f} + \frac{∂ \boldsymbol{g}}{∂ t} = - ∇ ⋅ \mathcal{J}\).
对于动量流密度张量, 其含义如下: 单位面积通过的动量密度.

辐射压力 \(P = \boldsymbol{e}_n ⋅ \mathcal{J} = 2 ω_i cos^2 θ \boldsymbol{e}_n\)

狭义相对论

洛仑兹变换, 四维形式

实验基础 (Michelson 实验)

在 Michelson 实验里面检测条纹移动个数 \(\frac{Δ l}{λ}\) 来判断是否有速度差.

并且在 Galileo 变换下, 尽管牛顿定律势协变的, 但是麦克斯韦方程并不是:

Galileo 变换下, \(\boldsymbol{v} = \boldsymbol{v}_1 + \boldsymbol{v}_2\), 理应对于波有波速的变化, 而电磁波波动方程 \(∇^2 \varphi - \frac{1}{c^2} ∂_t^2 \varphi = - ρ / ε_0\) 中的 \(\varphi, ρ, ε_0, c\) 无变化, 所以并不是协变的.

相对论基本假设:

相对性原理: 所有惯性参考系等价
光速不变原理: 真空中的光速相对与任何惯性系沿任意方向恒为 \(c\), 与光源运动无关.
(或者说等光程: \(Δ s^2 = c^2 Δ t^2 - Δ x^2 - Δ y^2 - Δ z^2\))

洛仑兹变换:

\[\begin{matrix} x' & = & \frac{x - v t}{\sqrt{1 - \frac{v^2}{c^2}}} \\ t' & = & \frac{t - \frac{v}{c^2} x}{\sqrt{1 - \frac{v^2}{c^2}}} \end{matrix} \quad ↔ \quad \begin{matrix} x & = & \frac{x' + v t'}{\sqrt{1 - \frac{v^2}{c^2}}} \\ t & = & \frac{t' + \frac{v}{c^2} x}{\sqrt{1 - \frac{v^2}{c^2}}} \end{matrix}\]

洛仑兹变换的一些结论

时空结构
- 光锥 (类光间隔) \(s^2 = 0\)
- 类时间隔 \(s^2 > 0\)
- 类空间隔 \(s^2 < 0\)
尺缩 \(Δ l = l_0 \sqrt{1 - \frac{v^2}{c^2}}\) (同时测量)
证明: \(Δ l = \frac{(x_1 - x_2)_{Δ l_0}}{\sqrt{1 - \frac{v^2}{c^2}}} = γ Δ l_0\)
时慢 \(Δ t = \frac{Δ t_0}{\sqrt{1 - \frac{v^2}{c^2}}}\) (同点测量)

一些相关的习题

在计算长度 \(Δ l\) 或者 \(Δ t\) 的时候, 需要考虑是否同时或者同点测量, 如果不是的话, 就要从最原始的公式: \(x' = γ (x - β c t), t' = γ (t - β x / c)\).
在 \(Σ\) 系中两个物体 \((u t, 0, 0)\), \((u t + l, 0, 0)\).

速度变换公式:

\[\begin{matrix} u_x' & = & \frac{u_x - v}{1 - \frac{v u_x}{c^2}} \\ u_y' & = & \frac{u_y \sqrt{1 - \frac{v^2}{c^2}}}{1 - \frac{v u_x}{c^2}} \end{matrix} \quad ↔ \quad \begin{matrix} u_x & = & \frac{u_x' + v}{1 + \frac{v u_x'}{c^2}} \\ u_y & = & \frac{u_y' \sqrt{1 - \frac{v^2}{c^2}}}{1 + \frac{v u_x'}{c^2}} \end{matrix}\]

四维形式:

表示的说明

在书中的四维矢量写作 \(\boldsymbol{r} = (r_x, r_y, r_z, i c t)\), 但是这种表示方法并不是很好用, 所以会选择一个常用的.

不过之间的差别应该不是太大, 把书中的 \(A_4\) 去掉 \(i\) 然后提到 \(A_0\) 就好.

四维位置矢量
\[\boldsymbol{r} = (c t, r_x, r_y, r_z) = (c t, \boldsymbol{r}_3)\]
一些说明
- 矢量的记号 \(A = (A_0, A_1, A_2, A_3) = [A^0, A^1, A^2, A^3]\)
- 内积
  \[A ⋅ B = A^{μ} η_{μ ν} B^{ν} = A_{μ} η^{μ\nu} B_{ν}\]
  
  对于四维位置矢量的 Minkowski 空间, 应当有 \(η_{μ\nu} = \left( \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{matrix} \right)\), 于是 \(Δ s^2 = c^2 t^2 - r_x^2 - r_y^2 - r_z^2 = A^{μ} η_{μ\nu} B^{ν}\).
- 导数 \(\mathrm{d} A = \frac{\mathrm{d} A}{\mathrm{d} λ} \mathrm{d} λ\), \(∂ = (\frac{1}{c} ∂_t, - ∇)\)
  于是可以计算速度
  
  \[\boldsymbol{v} = \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} τ} = \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t} \frac{\mathrm{d} t}{\mathrm{d} τ} = γ ⋅ (c, \boldsymbol{v}_3)\]
  
  其中 \(τ\) 为固有时 \(\frac{1}{c} {\mathrm{d} s}\), \(\boldsymbol{u}\) 为三维的运动速度, \(γ\) 为洛仑兹因子 \(γ = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}\).
  
  以及加速度
  
  \[\boldsymbol{a} = \frac{\mathrm{d} \boldsymbol{v}}{\mathrm{d} τ} = γ (\frac{\mathrm{d} γ}{\mathrm{d} t} c, \frac{\mathrm{d} γ}{\mathrm{d} t} \boldsymbol{u} + γ \boldsymbol{a}_3)\]
- 洛仑兹变换:
  \[A'^{μ} = Λ^{μ}_{ν} A^{ν}, A'_{μ} = Λ_{μ}^{ν} A_{ν}\]
  
  其中上面的记号为张量运算的符号, 而变换矩阵 \(Λ = \left( \begin{matrix} γ & - γ β & 0 & 0 \\ - β γ & γ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right)\), 假设沿 \(x\) 轴进行变换的矩阵.
  
  逆变换矩阵: \(Λ^{-1} = \left( \begin{matrix} γ & β γ & 0 & 0 \\ β γ & γ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right)\).
  
  验证和例子
  
  变换矩阵如此简单, 那么肯定很容易验证吧…
  
  (注: 变换矩阵还可以看成是一种绕着坐标轴进行旋转的操作: \(Λ = \left( \begin{matrix} cosh φ & - sinh φ & 0 & 0 \\ - sinh φ & cosh φ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right)\), 其中 \(γ = cosh φ\)).
  
  然后变换矩阵作用在位置矢量上的结果:
  
  \[r'_{μ} = Λ^{μ\nu} r_{ν} = (γ (c t - β x), γ(x - β c t), y, z)\]
  
  对于速度变换:
  
  \[v'_{μ} = Λ^{μ\nu} v_{ν}\]
  
  emm… 感觉怪怪的, 各种材料里面都没有太介绍的介绍.
四维动量
\[\boldsymbol{p} = γ (\frac{W}{c}, \boldsymbol{p}_3) = γ (\frac{p}{c}, \boldsymbol{f}_3)\]

其中 \(\boldsymbol{f}_3\) 为三维的力.

四维力

\[\boldsymbol{F} = m_0 \boldsymbol{a} = m_0 γ ⋅ (\frac{\mathrm{d} γ}{\mathrm{d} t} c, (\frac{\mathrm{d} γ}{\mathrm{d} t} \boldsymbol{u} + γ \boldsymbol{a}))\]

能量

\[W = T + m_0 c^2\]

有不变量:

\[p_{μ} p_{μ} = \frac{W^2}{c^2} - \boldsymbol{p}_3^2\]
电磁场
- 电流 \(\boldsymbol{j} = (ρ c, \boldsymbol{j}_3)\)
- 四维势 \(\boldsymbol{A} = (\frac{φ}{c}, \boldsymbol{A}_3)\)
  电磁场张量
  
  \[F_{μ\nu} = ∂_{μ} A_{ν} - ∂_{ν} A_{μ} = \left( \begin{matrix} 0 & - \frac{E_1}{c} & - \frac{E_2}{c} & - \frac{E_3}{c} \\ \frac{E_1}{c} & 0 & - B_3 & B_2 \\ \frac{E_2}{c} & B_3 & 0 & - B_1 \\ \frac{E_3}{c} & - B_2 & B_1 & 0 \end{matrix} \right)\]
  
  电磁场的变换关系
  
  张量的变换关系 \(F'_{μ\nu} = Λ_{μ\lambda}Λ_{ν\tau} F_{λ\tau}\):
  
  \[\begin{matrix} E'_1 & = & E_1 & B'_1 & = & B_1 \\ E'_2 & = & γ (E_2 - v B_3) & B'_2 & = & γ (B_2 + \frac{β E_3}{c}) \\ E'_3 & = & γ(E_3 + v B_2) & B'_3 & = & γ (B_3 - \frac{β E_2}{c}) \end{matrix}\]
  
  或者更加简洁的形式:
  
  \[\begin{matrix} \boldsymbol{E}'_{\parallel} & = & \boldsymbol{E}_{\parallel} & \boldsymbol{B}'_{\parallel} & = & \boldsymbol{B}_{\parallel} \\ \boldsymbol{E}'_{\bot} & = & γ (\boldsymbol{E} + \boldsymbol{v} × \boldsymbol{B})_{\bot} & \boldsymbol{B}'_{\bot} & = & γ (\boldsymbol{B} - \frac{\boldsymbol{v}}{c^2} × \boldsymbol{E})_{\bot} \end{matrix}\]
  
  其中的平行和垂直是相对于运动方向的.
- 波矢 \(\boldsymbol{k} = (\frac{ω}{c}, \boldsymbol{k}_3) ⇒ \boldsymbol{p} = \hbar \boldsymbol{k} = \hbar (\frac{ω}{c}, \boldsymbol{k}_3)\) 波动量
  相对论 Doppler 效应
  
  对波矢做 Lorentz 变换:
  
  \[k'_{μ} = Λ^{μ\nu} (\frac{ω}{c}, \boldsymbol{k}_3) = (\frac{γ (ω - β k_1 c)}{c}, γ (k_1 - \frac{β ω}{c}), k_2, k_3)\]
  
  于是可以得到 \(ω' = γ (ω - β k cos θ c)\), 其中 \(k_1 = k cos θ\).
  
  于是得到静止系上看到的频率 \(ω = \frac{ω'}{γ (1 - β cos θ)}\).
- 电磁场不变量
  \[\frac{1}{2} F_{μ\nu} F_{μ\nu} = B^2 - \frac{1}{c^2} E^2\]
- 电磁力
  \[f_{μ} = F_{μ\nu} J_{ν}\]

计算考虑相对论的电磁辐射

电偶极子 \(\boldsymbol{p}\) 做 \(v\) 匀速运动:
- 在 \(Σ'\) 系中的 \(\varphi' = \frac{\boldsymbol{p} ⋅ \boldsymbol{r}'}{4 π ε_0 r'^3}\), \(\boldsymbol{A}' = 0\), 四维势矢量 \((\varphi / c, \boldsymbol{A}')\) 做变换得到: \((γ \varphi / c, β γ \varphi / c, 0, 0)\).
- 在 \(Σ'\) 系中的电场 \(\boldsymbol{E}' = ∇ × \varphi = \frac{γ}{4 π ε_0 r'^3} (3 \frac{(\boldsymbol{p} ⋅ \boldsymbol{r}') \boldsymbol{r}'}{r'^2} - \boldsymbol{p})\), \(\boldsymbol{B}' = 0\).
- 需要做 \(\boldsymbol{r}' → \boldsymbol{r}\) 的一个操作.
无限长均匀带电 \(λ\) 直线以 \(v = β c\) 匀速运动, 计算点电荷 \(q\) 在 \(d\) 处受力:
1. \(Σ'\) 系中:

注

整完了之后发现上面的上下标都乱用了… 懒得改了, 差不多得了.

指标的一个说明

应该类似于 \(\boldsymbol{A} = A^i \boldsymbol{e}_i\) 这么个感觉, 其中 \(\boldsymbol{e}_i\) 为基底, \(A^i\) 为投影在基底上的分量的大小这样的感觉.

虽然确实应该怪我线性代数没有学好, 但是这东西讲得也确实很乱啊…

电磁相互作用

运动势和辐射场, 反作用

计算运动带电粒子的势:

\[\begin{matrix} \varphi(\boldsymbol{r}, t) & = & ∫_V \frac{ρ(\boldsymbol{r}', t - \frac{r}{c})}{4 π ε_0 r} \mathrm{d}V' \\ \boldsymbol{A}(\boldsymbol{r}, t) & = & ∫_V \frac{μ_0 \boldsymbol{J}(\boldsymbol{r}', t - \frac{r}{c})}{4 π r} \mathrm{d}V' \end{matrix}\]

对于低速运动的粒子, 可以近似认为是偶极辐射.

习题

\(z = z_0 e^{- i ω t}\) 的辐射场 (低速振动)
\(\boldsymbol{p} = - i z_0 ω q e^{- i ω t} ⇒ \boldsymbol{A} = \frac{μ_0 e^{i k r}}{4 π r} \dot{\boldsymbol{p}} = - \frac{μ_0 e^{i k r}}{4 π r} z_0 ω^2 q e^{- i ω t}\), 磁场 \(\boldsymbol{B} = ∇ × \boldsymbol{A} = - i k \frac{μ_0 z_0 q ω^2}{4 π r} e^{i (k r - ω t)} \boldsymbol{e}_r × \boldsymbol{e}_z\).

(注: 上面的这个计算还要考虑推迟效应, 但是如果是自场的话, 可以忽略.)

自场: 带电粒子周围的场, 可以忽略推迟效应.
辐射偏振

带电粒子辐射的反作用

辐射阻尼
\[\boldsymbol{F}_s = \frac{q^2}{6 π ε_0 c^3} \ddot{\boldsymbol{v}}\]
谱线自然宽度
\[Δ λ = \frac{2 π c}{ω^2} γ\]

习题

考虑阻尼力的运动轨道
\[m \ddot{\boldsymbol{r}} = q (\boldsymbol{E} + \dot{\boldsymbol{r}} × \boldsymbol{B}) + \frac{e^2}{6 π ε_0} \dddot{\boldsymbol{r}}\]

一般求解的话, 若只有磁场的二维运动, 可以考虑 \(u = x + i y\) 的解法.

以及电磁辐射: 因为变速运动, 所以 \(\dot{\boldsymbol{p}} = q \ddot{\boldsymbol{r}}\), 可以用偶极子辐射公式.

切伦科夫辐射

介质中带电粒子运动速度比介质中光速要快时, 便会产生切伦科夫辐射.
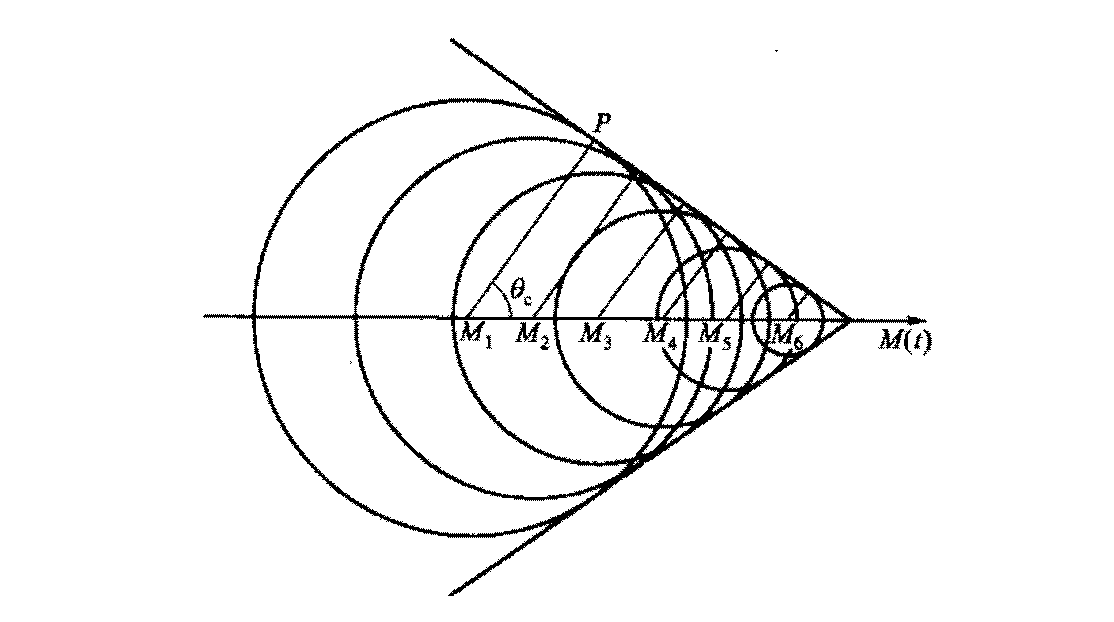
辐射方向 \(cos θ_c = \frac{c}{n v}\)
辐射能量角分布
\[\begin{matrix} \frac{\mathrm{d}^2 W_{ω}}{\mathrm{d} Ω \mathrm{d}L} & = & \frac{q^2 ω^2 n}{8 π^2 ε_0 c^3} sin^2 θ δ(\frac{ω}{v} - \frac{ω n}{c} cos θ) \\ & = & \frac{q^2 ω^2 n}{8 π^2 ε_0 c^3} (1 - \frac{c^2}{n^2 v^2}) δ(\frac{ω}{v} - \frac{ω n}{c} cos θ) \end{matrix}\]

辐射的总能量

\[\frac{\mathrm{d} W_{ω}}{\mathrm{d} L} = \frac{q^2}{4 π ε_0 c^2} [1 - \frac{c^2}{v^2 ε(ω)}] ω\]

电动力学 [期末]