复变函数 (期末)
复变函数
复数的运算
复数的表示方式
- $˜{z} = a + b \boldsymbol{i}$
- $˜{z} = ρ e^{\boldsymbol{i} π θ}$
- 欧拉公式: $e^{\boldsymbol{i} θ} = cos θ + sin θ$,
将两种表达方式连接在一起.
利用这个公式可以用来方便计算三角函数: Eg.
$$tan n φ = \frac{C_n^1 tan φ - C_n^3 tan^3 φ + C_n^5 tan^5 φ + \cdots}{C_n^0 - C_n^2 tan^2 φ + C_n^4 tan^4 φ + \cdots}$$
以 $sin n φ$ 为例, 只需要: $sin n φ = \mathrm{Im}(cos φ + \boldsymbol{i} sin φ)^n$, 如是即可.
- 或者是做球极投影
根据这样的两种不同的表示方式, 然后有对应的计算方法.
代数基本定理
农民说法: 在 $\mathbb{C}$ 上的多项式方程一定有根. 根的形式类似于 $f(x) = ∏ (x - x_i)^{α_i}$ 为 $α_i$ 重根.
一般用来计算根的情况.
计算多项式的根和分解因式:
$$P(z) = z^3 - z^2 + z + λ + 1$$
- 是否告诉了根? 假如知道 / 或者猜出来了一个根 $z = -i$, 那么就带进去, 化简 (没错, 就是用极 low 的长除法).
- 如果能化简到 $(x - x_i)^α$ 的形式, 结束, 否则, 重复第一步.
复变函数以及函数的性质 ( $\mathbb{C}$ 下)
计算复变函数 (多值性注意)
实际上只需要注意有多值性的那么几个函数即可.
- $\mathrm{ln}z = (\mathrm{Arg} z + 2 n π)\mathrm{ln}|z|$
- $\mathrm{arg}z = \mathrm{Arg} z + 2 n π$
需要了解的名词:
- 黎曼面, 割线: 通过黎曼面 (割线) 将复平面分割成多个单值平面
- 主值
- $n$ 阶枝点
以及一些特殊的函数的展开表达:
- $sin z = \frac{e^{iz} - e^{-iz}}{2i}, cos z = \frac{e^{iz} + e^{-iz}}{2i}$
实际上可以用欧拉公式来推导出来.
- $\mathrm{sinh} z$ 和 $\mathrm{cosh}$ 可以看作是把 $sin$ 和 $cos$ 里面的所有的 $i$ 变成 $1$.
在求根的时候, 会有类似于: $x = \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}}$ 这样的东西, 尽管通过 $x = \sqrt{1 + x}$ 的方式可以解决, 但是可能可以考虑多值性的结果.
解析函数
根据表达方式的不同, CR 条件有 x-y 和极坐标系的表示方式.
简单记忆方式: $u, v$, $x, y$, $ρ, θ$, 顺序为同号, 逆序为异号:
$$\frac{∂ u}{∂ x} = \frac{∂ v}{∂ y}, \frac{∂ u}{∂ y} = - \frac{∂ v}{∂ x}$$
并且 CR 条件和调和函数可以相互推导.
通过这个方式, 可以做到在已知 $u$ 或者 $v$ 的情况下, 计算另一半:
- 通过 CR 条件来:
- 已知 $u$ (为例),
- 通过 CR 条件计算得到 $∂_{x} v, ∂_{y} v$,
- 然后用解一般一阶偏微分方程的方式来得到 $v$, 这个方法有点类似于路径积分和保守场的感觉.
- 通过凑全微分来
- 已知 $u$ (为例)
- 计算得到 $∂_x v$ 和 $∂_y v$
- 写出 $\mathrm{d} v = ∂_x v \mathrm{d}x + ∂_y v \mathrm{d}y = \mathrm{d}(exp)$
- 代数方法
一般来说, 上面的应用的地方就是已知 等位线 $u$, 计算 势函数 $v$ 或者计算复势 $f = u + i v$.
积分和微分
柯西公式
$$f(x) = \frac{1}{2 π i}\oint \frac{f(ξ)}{ξ - x} \mathrm{d} ξ$$
实际上建立在环路积分以及和路径无关的解析函数的条件上.
微分
求导就和实数的求导是一样的. 不过可以通过柯西积分来变得更加有意思一点:
$$f(x) = \frac{1}{2 π i} \oint \frac{f(ξ)}{ξ - x} \mathrm{d}ξ ⇒ f'(x) = \frac{1}{2 π i} \oint \frac{f(ξ)}{(ξ - x)^2} \mathrm{d}ξ$$
这样就有了高阶导数.
比如利用柯西公式的高阶导数计算:
$$ψ(t, x) = e^{2 t x - t^2} ⇒ \frac{∂^n ψ}{∂ t^n} = (-1)^n e^{x^2} \frac{\mathrm{d}^n}{\mathrm{d} x^n} e^{-x^2}$$
在带入柯西公式计算的时候, 将 $η = ξ - x$ 带入.
积分
普通的积分和实数的部分基本一样. 满足线性, 以及积分区域的可加减.
主要关心的是有关柯西公式的积分, 具体的在留数定理那部分展开.
幂级数展开
收敛性
- 判断收敛性
- 比较法
- 看收敛半径是否存在
- 计算收敛半径 $R$, 收敛圆
一般的操作是这样的:
- $R = lim_{k → ∞} \frac{|a_k|}{|a_{k + 1}|}$
- $1 / R = lim_{k → ∞}\sqrt[k]{a_k}$
泰勒级数
$$f(x) = ∑_{i = 0}^{∞} = \frac{f^{(n)} (x_0) (x - x_0)^n}{n!}$$
展开方式和下文的洛朗级数合并.
常见的泰勒展开:
- $\mathrm{ln}z$ 在 $z = 1$ 附近展开:
$$\mathrm{ln}z = ∑_{k = 1}^{∞} \frac{(-1)^k (z - 1)^{k + 1}}{k + 1} + 2 π n i$$
- $(1 + z)^m$ 在 $z = 0$ 附近展开:
$$(1 + z)^m = ∑_{k = 1}^{∞} \frac{m(m - 1)(m - 2) \cdots (m - k + 1)}{k!} z^k$$
- $e^z$ 在 $z = 0$ 附近展开:
$$e^z = ∑_{k = 0}^∞ \frac{z^k}{k!}$$
- $sin z$ 和 $cos z$ 在 $z = 0$ 附近展开:
$$sin z = ∑_{k = 0}^∞ \frac{(-1)^k z^{2k + 1}}{(2k + 1)!}, cos z = ∑_{k = 0}^∞ \frac{(-1)^k z^{2k}}{(2k)!}$$
洛朗级数
农民理解: 在泰勒级数的基础上, 向反方向展开. 即对奇点做挖孔处理, 然后在孔外做泰勒展开, 在孔内做变换 $x \mapsto ξ = \frac{1}{x}$, 对 $ξ$ 进行泰勒展开, 然后再做一个解析延拓, 将两个方向的展开拼在一起.
展开的形式如下:
$$f(x) = \cdots + a_{-1} \frac{1}{x - x_0} + a_0 + a_1 x + \cdots$$
需要了解的概念:
- 孤立奇点的分类
- 可去奇点: $a_{-k}$ 项不存在.
- 本性奇点: $a_{-k}$ 有无穷多项, (在计算留数的时候会很麻烦), 一般常见的本性奇点可能会出现在 $0$ 或者 $∞$ 处, 尤其是后者, 不能忽略掉.
- 极点, $n$ 阶极点: 最多到 $a_{-n}$ 的奇点.
其中称一阶极点叫做单极点.
展开方式:
- 确认是否有奇点, 如 $\frac{1}{(x - x_i)^α}$ 这样的. 如果有, 需要在正常泰勒展开后准备洛朗展开.
- 对无奇点的区域进行泰勒展开:
- 如果是多项式, 简单的能求导的函数, 直接带入泰勒展开的公式即可.
- 如果是复杂的嵌套函数, 如 $\mathrm{ln}(1 + e^z)$ 这样的, 可以利用已经有的公式来展开.
- (如果有必要), 对有奇点 $z_0$ 的区域进行洛朗展开:
- 如果能够分解因式, (对于类似于有理多项式),
对其分解因式后变成类似于 $\frac{F(z)}{G(z) (z - z_0)^α}$
这样的形式, 其中 $F(z), G(z)$ 没有奇点, 或者不是 $z_0$ 奇点,
那么就对 $\frac{F(z)}{G(z)}$ 进行泰勒展开.
良好的结果就是能够展开.
- 变换 $\frac{1}{z - z_0} \mapsto ξ$, 然后对 $ξ$ 进行泰勒展开
- 如果能够分解因式, (对于类似于有理多项式),
对其分解因式后变成类似于 $\frac{F(z)}{G(z) (z - z_0)^α}$
这样的形式, 其中 $F(z), G(z)$ 没有奇点, 或者不是 $z_0$ 奇点,
那么就对 $\frac{F(z)}{G(z)}$ 进行泰勒展开.
留数定理及其应用
计算留数
- 如果知道洛朗展开的话, $a_{-1} = \mathrm{Res}f(z)$
- 如果知道其他奇点的留数, 但是缺一个留数, 利用留数定理:
$$\oint_l f(z) \mathrm{d}z = 2π i ∑_{j = 1}^n \mathrm{Res}f(b_j)$$
一般这样的方式是这样操作的: 通过计算一个 $\oint_l = 0$ 的环路, 然后把其中的奇点全部扣出来: $∑ \mathrm{Res}f(b_j) = 0$, 于是就可以计算得到某些奇点了.
一般用于计算 $∞$ 处的奇点:
把有限处的所有孤立奇点放在一个逆时针的回路 $l$ 里面, 然后考虑无穷远的孤立奇点:
$$\oint_l f(z) \mathrm{d}z = 2 π i ∑ \mathrm{Res} f(b) = - 2 π i \mathrm{Res}f(∞)$$
或者用来计算本性奇点.
不过留数定理可以通过回路积分和扣奇点的方式来记忆, 所以应该不怕会忘了.
- 利用公式: (非常需要记住)
$$\mathrm{Res}f(z) = lim_{z → z_0}\frac{1}{(m - 1)!} \frac{\mathrm{d}^{m - 1}}{\mathrm{d} z^{m - 1}}[(z - z_0)^m f(z)]$$
通过洛朗级数展开没准可能会比用公式来的快?
- $f(z) = \frac{z^{2n}}{(z + 1)^n}$
因为目测奇点有一个在 $z = -1$, 所以用 $ξ = z + 1$ 来, 于是 $f(ξ) = \frac{(ξ - 1)^{2n}}{ξ^n}\ ⇒ a_{-1} = C_{2n}^{n+1} (-1)^{n + 1}$.
并且还要注意不要忽略了 $∞$ 的 (本性) 奇点. 利用留数定理即可计算.
留数定理和回路积分
留数定理原则上可以解决所有的回路积分. 即将回路积分变成求留数和的操作.
- 首先确认回路轨道以及轨道里面的奇点分布.
- 最简单的情况就是奇点安分守己地分布在回路轨道包含的区域里面
- 稍微麻烦一点的是如果奇点落在了轨道上 (区域的边界),
这个时候需要计算出这个奇点被包裹了多少的角度.
一般是一条直线直接通过, 这个时候包裹 $π$, 对应 $\frac{1}{2} \mathrm{Res}$. 如果是一个直角直接通过, 这个时候包裹 $π / 2$, 对应 $\frac{1}{4} \mathrm{Res}$. 抽象一点, 如果是一个 $θ$ 角通过, 这个时候包裹 $θ$, 对应 $\frac{θ}{2π}\mathrm{Res}$.
其他情况就比较难搞了, 一般不会构造这么离谱的路线. (通过计算路径的曲率圆半径 $ρ$, 计算路径的微分长度 $\mathrm{d}s$, 然后计算得到对应的圆内角 $δ$, 即可知道对应的 $θ = π - δ$)
- 以及不要忘了 $∞$ 处, 如果轨道通过的话…
- 计算奇点对应的留数
这个时候要考虑到前面的部分通过的情况 (如果需要考虑的话)
- 然后利用留数定理:
$$\oint f(z) \mathrm{d}z = 2 π i∑ \mathrm{Res}f(z)$$
利用留数定理计算:
- $\oint \frac{\mathrm{d}z}{(z^2 + 1)(z - 1)^2}, l: x^2 + y^2 - 2x - 2y = 0$
这种的就先画出路径, 然后标出奇点. 然后计算留数: $\mathrm{Res}f(i) = \frac{1}{2 i (i - 1)^2} = \frac{1}{4}$, $\mathrm{Res}f(1) = \frac{\mathrm{d}}{\mathrm{d} t}\frac{1}{z^2 + 1}|_1 = -\frac{1}{2}$.
于是利用留数定理: $\oint = -2 π i\frac{1}{4}$
- $\oint_{|z| = 2} \frac{z \mathrm{d}z}{1/2 - sin^2 z}$
其实关键还是如何计算这个留数. 可以通过 $(1 - 2sin^2 z) / 2 = (cos 2z) / 2$ 化简后得到: $\oint_{|u| = 1}\frac{u}{cos u} \mathrm{d}u$.
后者的留数通过求导可以计算得到.
留数定理和实变函数定积分
关于实变函数的部分, 一个简单的想法就是如何将实变函数的定积分 用一个复变函数的回路积分来表示, 表示完后在用留数定理计算回路积分:
- 三角函数的有理式
$$I = ∫_0^{2π} R(cos x, sin x)\mathrm{d}x$$
通过令 $cos x = \frac{z + z^{-1}}{2i}, sin x = \frac{z - z^{-1}}{2i}, \mathrm{d}x = \frac{\mathrm{d}z}{iz}$ 的方式, 来将实积分变成路径积分.
- $∫_{0}^{2π} \frac{\mathrm{d}x}{2 + cos x}$
带入一般结论: $\oint \frac{2}{1 + 4 i z + z^2} \mathrm{d}z$, 然后可以有 $z = -i(2 ± \sqrt{5})$.
然后带入计算留数即可.
- $∫_0^{π / 2}\frac{\mathrm{d}x}{1 + cos^2 x}$
像这种积分区域不完全的, 一般是想办法补成完全的.
- $∫_{0}^{2π} \frac{\mathrm{d}x}{2 + cos x}$
- $I = ∫_{-∞}^{∞} f(x)\mathrm{d}x$,
被积函数满足:
- 在实轴上没有奇点, 并且在上半平面有限个奇点外解析,
- 并且 $z$ 在上半平面及实轴上 $→ 0$ 时, $z f(x) → 0$
实际上就是利用 $-∞ → ∞ →$ 走一个 $R → ∞$ 的一个返回路线的一个半圆形积分回路.
但是因为 $z f(z) → 0$ 所以圆弧的路线积分 $→ 0$
- $∫_{-∞}^{∞} \frac{x^2 + 1}{x^4 + 1} \mathrm{d}x$
满足条件, 所以只需要关心上半平面的那两个留数 $\mathrm{Res} f(e^{iπ/4})$, 以及 $\mathrm{Res} f(e^{3iπ/4})$.
- $∫_0^∞ \frac{\mathrm{d}x}{x^4 + a^4} \mathrm{d}x$
类似这种的, 一般想办法先利用对称性什么的先补全.
- $∫_0^∞ F(x) cos m x \mathrm{d}x, ∫_0^∞ G(x) sin m x \mathrm{d}x$
其中:
- $F(x)$ 为偶函数, $G(x)$ 为奇函数
- 在实轴上无奇点, 在上半平面内
实际上关键在于利用这个奇偶函数然后做对称拓展积分区域, 还是构造一个积分路径.
留数定理和无穷级数求和
对于求和 $S = ∑_{n ∈ \mathbb{Z}} f(n)$, 若 $f(z)$ 满足在孤立奇点外解析, 并且 $|z| → ∞$ 的时候, $|f(z)| = \mathcal{O}(|z|^{-1-δ})$:
引入一个辅助函数 $g(z)$, 仅在 $n ∈ \mathbb{Z}$ 处有单极点, 且 $\mathrm{Res} g(n) = lim_{z → n} [(z - n) g(z)] = 1$. 于是可以构造 $F(z) = f(z) g(z)$.
于是可以利用留数定理来对来计算:
$$∑ f(z) = ∑ \mathrm{Res}F(z) = lim_{m → ∞} \frac{1}{2 π i} \oint F(z) \mathrm{d}z$$
傅里叶和拉普拉斯
傅里叶
对 $f(z)$ 进行傅里叶展开
记忆傅里叶展开公式:
$$f(x) = \frac{a_0}{2} + ∑ a_k cos \frac{k π x}{l} + b_k sin \frac{k π x}{l}$$
其中:
$$a_k = \frac{1}{δ_k l} ∫_{-l}^l f(x) cos \frac{k π x}{l}\mathrm{d}x$$ $$b_k = \frac{1}{l} ∫_{-l}^l f(x) sin \frac{k π x}{l} \mathrm{d}x$$
其中, $δ_k = 2 \mathrm{\ iff\ } k = 0 \mathrm{\ else\ } 1$.
不过可以通过对称性来简化计算, 如奇函数就可以不用考虑 $a_i$ 项, 偶函数就可以不用考虑 $b_i$ 项.
- 对 $|sin x|$ 进行傅里叶展开:
因为是偶函数, 并且区间是 $(-\frac{π}{2}, \frac{π}{2})$. 所以只需要积分 $b_k = ∫_{-π / 2}^{π / 2} sin x sin k x \mathrm{d}x$
一般这类积分通过分布积分即可积分得到. 实在不能的话, 可以利用留数定理来做.
- 带边界条件的部分展开, 一般是下面这样的几个展开:
- $f(0) = 0$ 一般将部分延拓成奇函数
- $f'(0) = 0$ 一般将部分延拓成偶函数
- 两者都不是, 但是可以通过平移变换变成奇函数或者偶函数. 直接平移变换即可.
对 $f(z)$ 进行傅里叶变换
硬搞的积分 (复数形式的傅里叶积分):
$$f(x) = \frac{1}{\sqrt{2π}} ∫_{-∞}^{∞} F(ω) e^{i ω x} \mathrm{d}ω$$
$$F(ω) = \frac{1}{\sqrt{2 π}} ∫_{-∞}^{∞} f(x) e^{-i ω x} \mathrm{d}x$$
(注: 实数形式的傅里叶积分略去. )
基本性质:
- 导数定理: $\mathcal{F}[f'(x)] = i ω F(ω)$
- 积分定理: $\mathcal{F}[∫^{(x)} f(ξ) \mathrm{d}ξ] = \frac{1}{i ω} F(ω)$
- 相似性定理: $\mathcal{F}[f(a x)] = \frac{1}{a} F(\frac{ω}{a})$
- 延迟定理: $\mathcal{F}[f(x - x_0)] = e^{-i ω x_0} F(ω)$
- 位移定理: $\mathcal{F}[e^{i ω x} f(x)] = F(ω - ω_0)$
- 卷积定理: $\mathcal{F}[f_1(x) * f_2(x)] = 2π F_1(ω) F_2(ω)$
其中, 卷积定理中的卷积定义为:
$$f_1(x) * f_2(x) = ∫_{-∞}^{∞} f_1(ξ) f_2(x - ξ) \mathrm{d}ξ$$
(并且如果忘了的话, 其实可以从傅里叶积分的定义快速回忆起来. )
应用
- 正交多项式
- 广义函数
拉普拉斯
对 $f(z)$ 进行拉普拉斯变换
直接代公式:
$$\bar{f}(p) = ∫_0^∞ f(t) e^{-p t} \mathrm{d}t$$
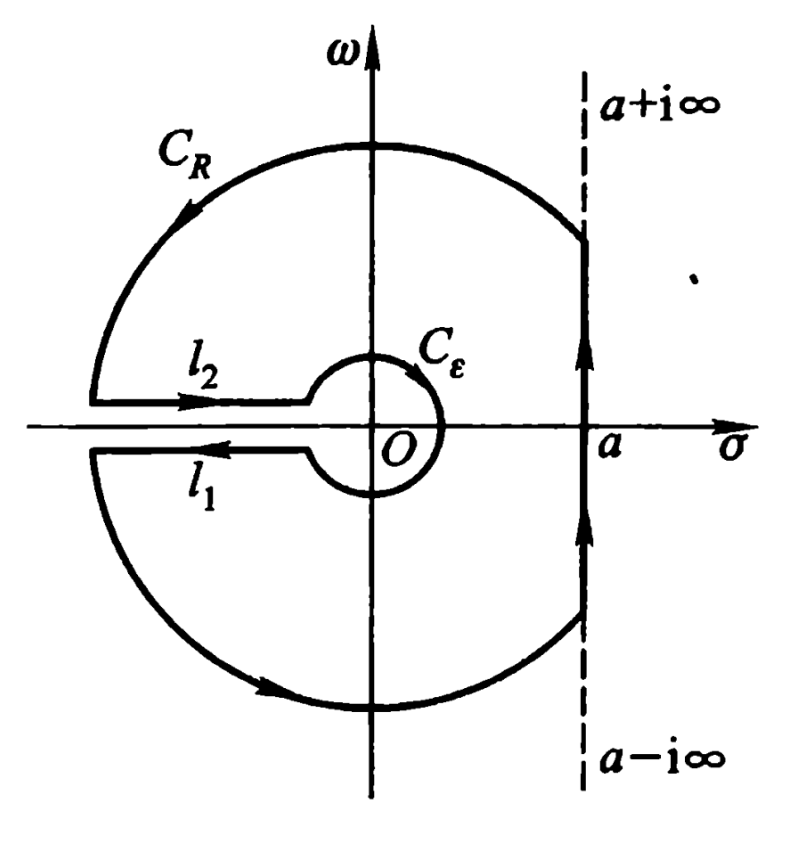
逆变换:
$$f(t) = \frac{1}{2 π i} ∫_{σ - ∞}^{σ + ∞} \bar{f}(p) e^{i p} \mathrm{d}p$$
直观的理解就是, 对于 $f(t → ∞) \nrightarrow 0$ 的函数, 乘上一个强制收敛因子 $e^{-σ t}$, 然后再进行 “傅里叶变换”.
令 $p = σ + i ω$, 就能够得到一个拉普拉斯变换了.
一些性质:
- 线性性: $c_1 f_1(t) + c_2 f_2(t) \fallingdotseq c_1 \bar{f}_1(p) + c_2 bar{f}_2(p)$
- 导数定理: $f'(t) \fallingdotseq p \bar{f}(p) - f(0)$
- 积分定理: $∫_0^t ψ(τ) \mathrm{d}τ \fallingdotseq \frac{1}{p} \mathcal{L}[ψ(t)]$
- 相似性定理: $f(a t) \fallingdotseq \frac{1}{a} \bar{f}(\frac{p}{a})$
- 位移定理: $e^{-λ t}f(t) \fallingdotseq \bar{f}(p - λ)$
- 延迟定理: $f(t - t_0) \fallingdotseq e^{-pt_0} \bar{f}(p)$
- 卷积定理: $f_1(t) * f_2(t) \fallingdotseq \bar{f}_1(p) \bar{f}_2(p)$
计算的 trick
一般通过查表的方式配合上面的性质来减少计算的复杂性.
但是考试不让查表, 所以可以先记住一些常用的:
- $t^n \fallingdotseq \frac{n!}{p^{n + 1}}$
- $e^{s t} \fallingdotseq \frac{1}{p - s},\ (\mathrm{Re\ } p > \mathrm{Re\ } s)$
- $t^n e^{s t} \fallingdotseq \frac{n!}{(p - s)^{n + 1}}$
- $t^n f(t) \fallingdotseq (-1)^n \frac{\mathrm{d}^n}{\mathrm{d} p^n} \bar{f}(p)$
- $\frac{p}{p^2 + ω^2} = cos ω t$
- $\frac{ω}{p^2 + ω^2} = sin ω t$
反演:
- 有理分式
一般想法是化简成 $\frac{a}{p - s} \risingdotseq a e^{s t}$, 或者是 $\frac{p}{p^2 + ω^2} \risingdotseq sin ω t$
- 查表配合定理
- 如果像函数是 $e^{-τ p} \bar{f}(p)$ 的形式, 那么使用延时定理. 还原的结果为 $f(t - τ)$.
- 如果像函数是 $\bar{f}(p - λ)$ 的形式, 那么使用位移定理. 还原的结果为 $e^{-λ t} f(t)$.
- 如果向函数是 $\bar{f}(p / a)$ 形式, 那么使用相似性定理. 还原的结果为 $a f(a t)$.
- 上面的可以配合使用.
- 黎曼-梅林反演公式, 其实就是上面的积分.
不过在积分的时候, 取路径为一个去掉奇点的一个圆.
解线性方程
利用导数定理可以将 $f^{(n)}(x) \fallingdotseq p^n \bar{f}(p)$, 然后就可以解出 $\bar{f}(p)$, 最后做反演即可.
$$y” + 4 y' + 13 y = 13$$
- 两边做变换: $(p^2 + 4 p + 13)\bar{y} = \frac{13}{p}$
- 解得 $\bar{y} = \frac{13}{p (p^2 + 4p + 13)}$$
- 反演得到 $y$ 的解
解积分方程以及求积分
利用积分定理可以用来处理积分问题:
- $∫_0^∞ \frac{sin t}{t}\mathrm{d}t$
方法不太理解 $sin ω t \fallingdotseq \frac{ω}{p^2 + ω^2}$, $∫_0^∞ e^{-pt} \mathrm{d}p = \frac{1}{t}$, 然后带入 $I = ∫_0^∞ \mathrm{d}t ∫_0^∞ \mathrm{d}p sin t e^{-p t} = ∫_0^∞ \frac{\mathrm{d}p}{p^2 + 1} = \frac{π}{2}$.