About

/_img/pieces/atomic-physics/high-frequency-cavity-aging-radiation-danger.jpg

(注: 图文无关, 只是科技开放日去高能所看见觉得很好玩… 孩子不懂事, 瞎拍着玩的)

哦, 伟大的圆环之理啊, 保我…

精细结构

  • 四个量子数: \(n, l, m_l, m_s\) 或者 \(n, l, j, m_j\).
  • 三个实验:
    • 碱金属双线
    • 塞曼效应
    • 施特恩-盖拉赫实验
  • 电子轨道运动: \(μ_l = - γ L = - \sqrt{l (l + 1)} \hbar γ = - \sqrt{l (l + 1)} \frac{e \hbar}{2 m_e}\), 其中角动量大小 \(L = \sqrt{l (l + 1)} \hbar\), \(γ\) 为角动量和磁矩的比.

    在外磁场下 \(L_z = m_l \hbar\), \(μ_{l, z} = - γ L_z = - \frac{e \hbar}{2 m_e} m_l\). 其中 \(m_l = ± l, ± (l - 1), …\) 为轨道角动量角分布量子化取值.

    角分布量子化取值实验验证: 施特恩 - 盖拉赫实验

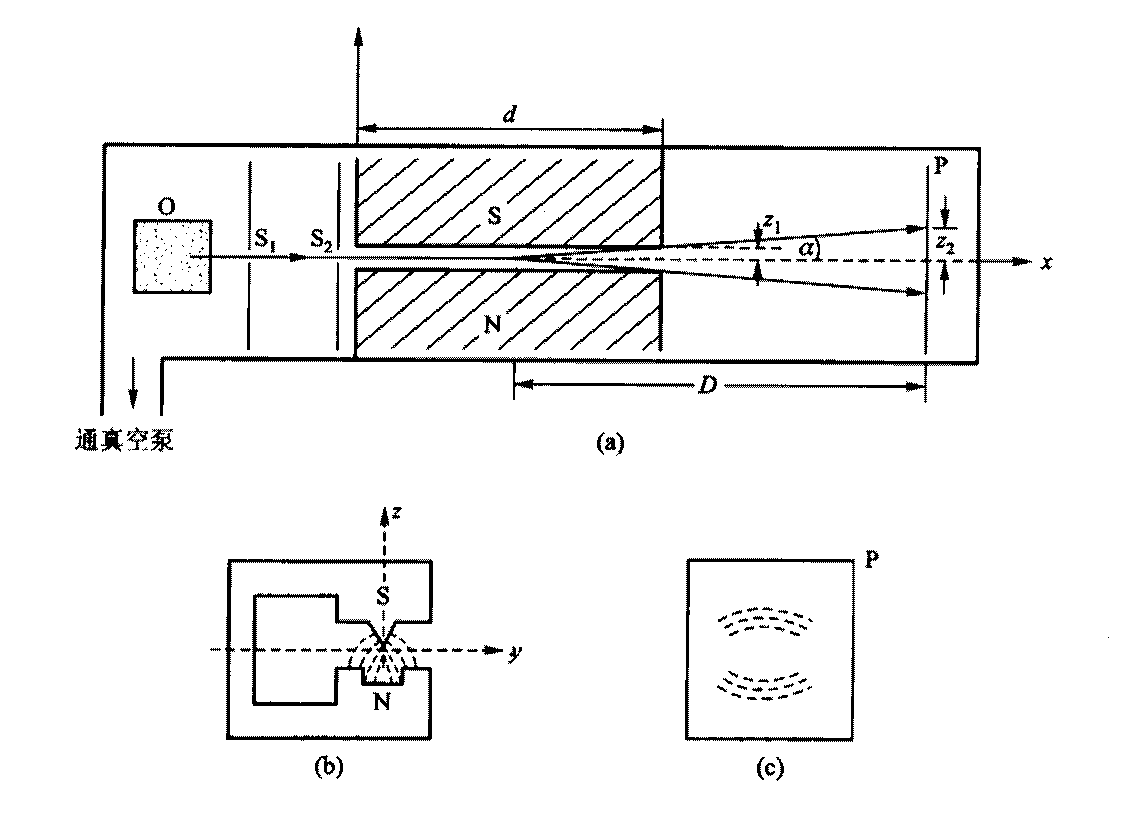
    /_img/pieces/atomic-physics/stern-gerlach.png

    • \(z\) 方向非均匀磁场, 使得 \(U = - \boldsymbol{μ} ⋅ \boldsymbol{B} ⇒ \boldsymbol{F} = - ∇ U\) 在 \(z\) 方向上会有偏移.
    • 根据 \(μ_{l,z} = - m_j g_j μ_B\), 可以知道最终会分裂成多少条谱线.

    可以简记为 \(μ_B = \frac{e \hbar}{2 m_e}\), \(μ_l = - \sqrt{l (l + 1)} μ_B\), \(μ_{l, z} = - m_l μ_{B}\).

    习题
    • 根据磁矩计算能量差 \(Δ E = Δ \boldsymbol{μ} ⋅ \boldsymbol{B}\)

      \(\boldsymbol{μ} ⋅ \boldsymbol{B} = g_s m_s μ_B B\), 对于电子 \(g_s = 2, m_s = ± \frac{1}{2}\).

    • 根据原子态计算磁矩 原子态: \(^{2S + 1}L_J\)

      首先获得 \(S, L, J\) 的值, 然后计算得到 \(m_J\). 然后计算磁矩 \(μ_J = - g_J \sqrt{J (J + 1)} μ_B, μ_{J,z} = - m_J g_J μ_B\).

      (注: 如果已经得到磁矩了的话, 可以根据磁矩来算梯度场中的受力, 然后根据这个受力来进行计算谱线分离.)

      一些代码 
      (defun sym-l (sym)
  (cond ((eq sym 'S) 0)
        ((eq sym 'P) 1)
        ((eq sym 'D) 2)
        ((eq sym 'F) 3)
        ((eq sym 'G) 4)
        ((eq sym 'H) 5)
        ((eq sym 'I) 6)
        (T sym)))               ; I'd bad in Lisp

(defun l-sym (l)
  (cond ((eq l 0) 'S)
        ((eq l 1) 'P)
        ((eq l 2) 'D)
        (T (intern (string (code-char (+ l 67)))))))

      (defun lande-g-factor (atom-state)
  "ATOM-STATE: (2S+1 L J) -> Gj = 3/2 + (S(S + 1) - L(L + 1)) / (2J(J+1))."
  (let ((s (/ (1- (first atom-state)) 2))
        (l (sym-l (second atom-state)))
        (j (third atom-state)))
    (+ 3/2 (/ (- (* s (1+ s)) (* l (1+ l)))
              (* 2 j (1+ j))))))

      (defun m-j-lst (j)
  "mJ: ±J, ±(J - 1), ..."
  (loop for mj from j downto (- j) collect mj))
  • 电子自旋: 电子自旋角动量 \(S = \sqrt{s (s + 1)} \hbar\), \(s = \frac{1}{2}\). 在磁场 \(z\) 方向上 \(s_z = ± \frac{1}{2} \hbar = m_s \hbar, m_s = ± \frac{1}{2}\).
  • \(g_j\) 朗德 g 因子: \(g = \frac{\mathrm{measured}\ μ_z\ \mathrm{united\ in}\ μ_B}{z\ \mathrm{projection\ of}\ L\ \mathrm{united\ in}\ \hbar}\).

    通过 \(g\) 因子可以将自旋磁矩写成通用的形式: \(μ_j = - g_j μ_B \frac{S}{\hbar} = - \sqrt{j (j + 1)} g_j μ_B\), \(μ_{j,z} = - m_j g_j μ_B\).

    对于电子: \(μ_s = - \frac{g_s μ_B}{\hbar} S, μ_{s, z} = - m_s g_s μ_B\), 并且 \(g_s\).

    一些更多的解释和计算

    原子磁矩 \(≅\) 电子轨道磁矩 \(+\) 电子自旋磁矩 (\(\boldsymbol{μ} = \boldsymbol{μ}_l + \boldsymbol{μ}_s\))

    轨道角动量 \(L = \sqrt{l (l + 1)} \hbar, l = 0, 1, …, n - 1\), 电子自旋角动量 \(S = \sqrt{s(s + 1)} \hbar, s = \frac{1}{2}\). 总角动量 \(\boldsymbol{J} = \boldsymbol{L} + \boldsymbol{S} ⇒ \boldsymbol{μ}_l = - \frac{e}{2 m} \boldsymbol{L}\).

    为了简化表示, 通过 \(^{2S + 1}L_J\) 来表示原子状态, 其中 \(L\) 为轨道角动量对应的量子数, \(L: [S, P, D, F, G, …] → [0, 1, 2, 3, …]\). \(S\) 为自旋对应的量子数, \(J\) 为总角动量对应的量子数.

    于是可以计算 \(g_J = \frac{3}{2} + \frac{1}{2} \frac{S^2 - L^2}{J^2}\).

    于是可以计算 \(m_j g_j\), 得到最终谱线的分裂.

  • 双线结构
    • 原子实 和 价电子

      对碱金属原子的基态: 底层轨道填满, 然后留下一个在外头的电子. 尽管应当和氢原子很像和 \(l\) 有关, 但是因为 轨道贯穿 和 原子实极化, 导致能级还和 \(l\) 有关.

    • 跃迁选择定则 \(Δ l = ± 1, Δ j = 0, ± 1\)
    • 精细结构 和 超精细结构

      修正磁矩的影响, 加入由于自旋-轨道相互作用产生的: 精细结构 (自旋磁矩和轨道磁矩), 超精细结构 (原子核磁矩和电子磁矩).

      自旋-轨道相互作用

      大概就是换系, (角动量, 圆周运动) 运动产生磁场, 磁场对自旋磁矩产生的能量.

      那么如何估算磁场?

      计算能量差 \(Δ U ⇒ U = g_s m_s μ_B B\), 选择已知的不同谱线进行计算.

    • 兰姆移位
  • 塞曼效应

    \[h Δ ν = Δ (m_j g_j - m_i g_i) μ_B B\]

    具体的一些说明

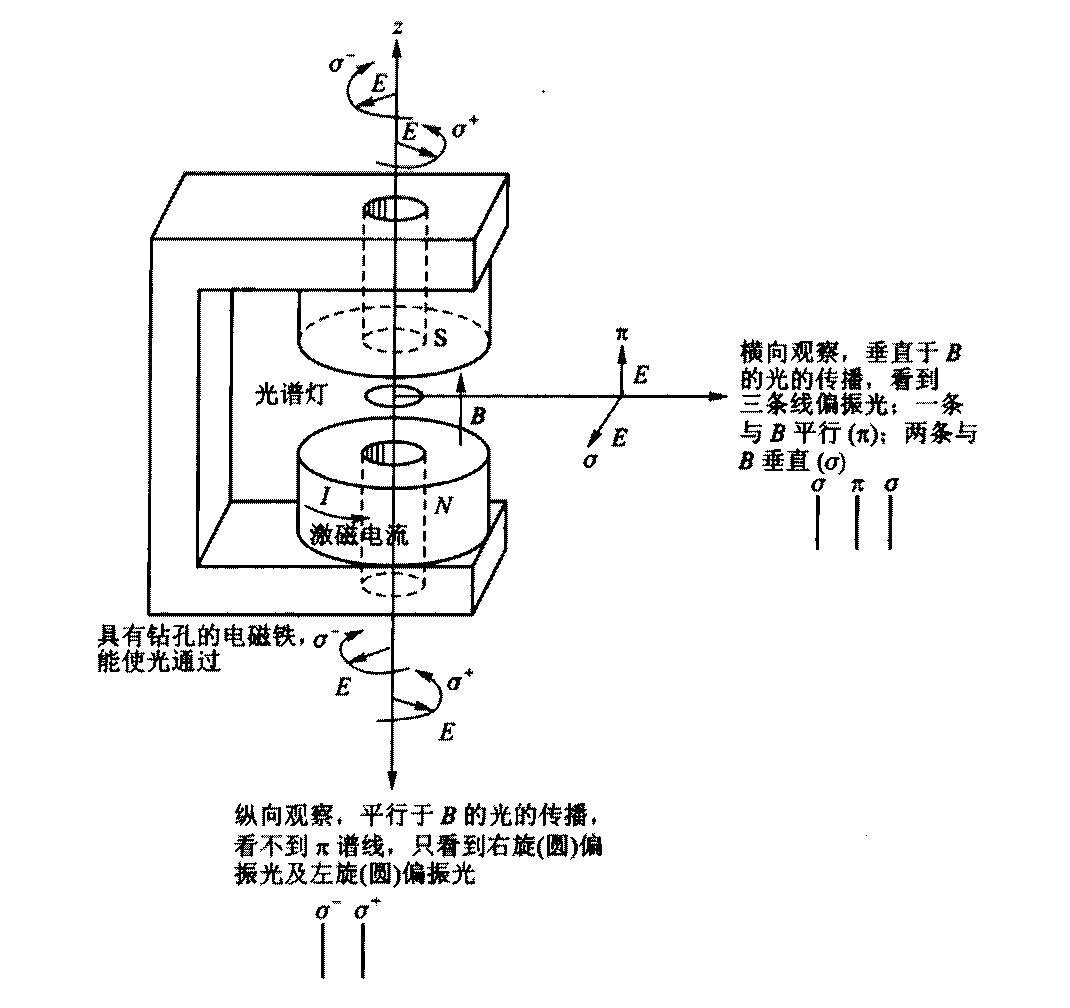
    /_img/pieces/atomic-physics/zeeman-exp.png

    如果要出现正常塞曼效应, 则需要原子形成 \(s = 0, 2 s + 1 = 1\) 的独态. 所以对于 \(^1L_j\) 的原子可行.

  • 斯塔克效应
  • 核磁共振
习题
  • 格罗春图
  • 计算跃迁谱线波长

多电子原子

  • 泡利原理
  • 洪特定则

电子耦合

  • 电子组态
  • 双电子耦合 (氢原子)

    将多电子的自旋和轨道角动量记作 \(S = (s_1, s_2, s_3, …)\) 和 \(L = (l_1, l_2, l_3, …)\)

    • \(L-S\) 耦合 \((S, L) = J\)
      更加详细的计算

      将原子态表示为 \((n_1 l_1 n_2 l_2)^{2s + 1} L_j\), 于是可以计算得到系统的 \(s = 0, 1\); \(l = l_1 + l_2, l_1 + l_2 - 1, …, |l_1 - l_2|\); \(j = l + s, l + s - 1, …, |l - s|\).

      于是应当可以历遍得到原子态符号: \(^{2s+1}L_j\).

      计算过程 
      (defun L-S-states (l1 s1 l2 s2)
  (let* ((l-1   (sym-l l1))
         (l-2   (sym-l l2))
         (L-lst (loop for l from (+ l-1 l-2) downto (abs (- l-1 l-2)) collect l))
         (S-lst (loop for s from (+ s1 s2) downto 0 collect s))
         (res   '()))
    (loop for s in S-lst do
          (loop for l in L-lst do
                (loop for j from (+ l s) downto (abs (- l s)) do
                      (push (list (+ 1 (* 2 s)) (l-sym l) j) res))))
    res))

      (L-S-states 'p 1/2 'd 1/2)

      ((1 P 1) (1 D 2) (1 F 3) (3 P 0) (3 P 1) (3 P 2) (3 D 1) (3 D 2) (3 D 3) (3 F 2) (3 F 3) (3 F 4))

    • \(j-j\) 耦合 \((s_1 l_1)(s_2 l_2)… = (j_1, j_2, j_3, …) = J\)
      详细的说明和计算步骤
      1. 还是一样, 计算得到量子数 \(l, s, j\), 于是可以计算 \(m_j\)
      2. 由于泡利不相容, 所以同样状态的 \(n, l, j, m_j\) 只能有一个

    在这样的耦合系统中, 从状态 \((S, L)\) (或者 \(J\)) 变换到状态 \((S', L')\) (或者 \(J'\)), 应当满足选择规则:

    • \(L-S\) 耦合: \(Δ S = 0; Δ L = 0, ± 1; Δ J = 0, ± 1 (J = 0 ¬\rightarrow J' = 0)\)
    • \(j-j\) 耦合: \(Δ j = 0, ±1; Δ J = 0, ± 1(J = 0 ¬\rightarrow J' = 0)\)
  • He 原子能级
习题
  • 计算对应态的 \(\boldsymbol{L} ⋅ \boldsymbol{S}\): (\(\boldsymbol{L} - \boldsymbol{S}\) 耦合)
    1. 得到 \(s, j, l\) (量子态)
    2. 计算 \(S = \sqrt{s(s + 1} \hbar, L = \sqrt{l(l + 1)} \hbar, J = \sqrt{j(j + 1)}\hbar\) (角动量)
    3. 利用耦合关系 \(\boldsymbol{J}^2 = (\boldsymbol{L} + \boldsymbol{S})^2 = \boldsymbol{L}^2 + \boldsymbol{S}^2 + 2 \boldsymbol{L} ⋅ \boldsymbol{S}\) 计算
  • 计算可能存在的原子态
    • 考虑 \(L-S\) 耦合: (L-S-state l1 s1 l2 s2), 并且对于同科电子, 由于泡利原理, 只有 \(l+s\) 为偶数的电子存在.
      代码

      偶数定则是由于同科电子 (\(n\) 和 \(l\) 都相同的电子引入的限制)

      (defun even-rule (atom-state)
  "L+S should be even."
  (let ((s (/ (1- (first atom-state)) 2))
        (l (sym-l (second atom-state))))
    (evenp (+ s l))))

      (defun n-l-eq-e-possible-states (l)
  (remove-if-not #'even-rule (L-S-states l 1/2 l 1/2)))

      (n-l-eq-e-possible-states 'd)

      ((1 S 0) (1 D 2) (1 G 4) (3 P 0) (3 P 1) (3 P 2) (3 F 2) (3 F 3) (3 F 4))

    • 考虑 \(j-j\) 耦合

泡利不相容原理

在一个原子中, 不可能有两个或者两个以上的电子据有完全相同的四个量子数 \((n, l, m_l, m_s)\). 或者更加一般地说: 在全同费米子 (自旋为半整数的粒子) 组成的系统中不能有两个或者多个粒子处于完全相同的状态.

全同费米子

在 热统 里面已经遇到过了. 交换两个全同粒子, 其波函数是否改变? (交换对称或者交换反对称) 若对称, 则是 玻色子; 若反对称, 则为 费米子.

对于反对称的费米子, 则会有 \(ψ(α, β)\) 会使得 \(α, β\) 不相同.

元素周期表

  • 电子 壳层 (\((K, L, M, N, O, P, Q, …) → (1, 2, …)\)) 和 支壳层 (\((s, p, d, f, g, h, i, …) → (0, 1, 2, …)\)).

    填充原则:

    • 支壳层能够容纳的电子数 \(2(2l + 1)\), 壳层能够容纳的电子数 \(N = ∑ 2 (2l + 1) = 2 n^2\).
    • 能量最小 (从低开始填)
      壳层次序和洪特定则

      壳层次序:

      填充顺序: \(1s, 2s, 2p, 3s, 3p, 4s, 3d, …\) 定性的解释就是对于圆轨道 \(3d\) 没有轨道贯穿和极化效应, 而 \(4s\) 轨道在径向扭曲, 靠近原子核处拉低了能量.

      代码 
      (defun electron-shell-next (electron)
  "ELECTRON (n . l): (1 . s) -> (2 . s)"
  (let ((n (car electron))
        (l (sym-l (cdr electron))))
    (if (zerop l)                       ; l = s
        (cond ((eq n 1) (cons 2 's))
              ((eq n 2) (cons 2 'p))
              ((eq n 3) (cons 3 'p))
              (T (cons (- n (floor (/ (- n 2) 2))) ; not sure...
                       (l-sym (floor (/ n 2))))))
        (cons (1+ n) (l-sym (1- l))))))

      (loop for - upto 10
      with electron = (cons 1 's)
      collect electron
      do (setq electron (electron-shell-next electron)))

      ((1 . S) (2 . S) (2 . P) (3 . S) (3 . P) (4 . S) (3 . D) (4 . P) (5 . S) (4 . D) (5 . P))

      洪特定则:

      1. 给定电子组态, 能量最低的原子态必定具有泡利不相容原理所允许的最大 \(S\) 值.
      2. \(S\) 值相同状态, \(L\) 值最大的原子态能量最低
      3. 对于同科电子 \((nl)^{ν}\):
        • \(ν \leq 2 l + 1\), \(J\) 最小的能量最低
        • \(ν > 2 l + 1\), 超过半满, \(J\) 最大能量最低
      例题: 根据 \(Z\) 来确定基态原子态符号
      1. 根据 \(Z\) 来确定电子组态
        代码 
        (defun electron-shell-of-z (z)
  "Z -> 1s2 2s2 ... (((1 . s) . 2) ((2 . s) . 2) ...)"
  (labels ((n-shell (shell)                 ; shell: (n . l)
             (let ((l (sym-l (cdr shell)))) ; n-shell = 2(2l + 1)
               (* 2 (1+ (* 2 l))))))
    (loop with e-shell = (cons 1 's)
          with counter = 0
          with res     = '()
          while (< counter z) do
            (let ((inc (min (- z counter) (n-shell e-shell))))
              (push (cons e-shell inc) res)
              (setq counter (+ counter inc)
                    e-shell (electron-shell-next e-shell)))
          finally (return (sort res #'< :key #'caar)))))

        (electron-shell-of-z 26)                ; Fe

        (((1 . S) . 2) ((2 . P) . 6) ((2 . S) . 2) ((3 . D) . 6) ((3 . P) . 6) ((3 . S) . 2) ((4 . S) . 2))
      2. 根据洪特定则 (1), 使得 \(S\) 最大

        这个时候就不看那些被排满的电子, 而是看没有被排满的电子.

      3. 根据洪特定则 (2), 使得 \(L\) 最大 (考虑泡利原理)
      4. 根据洪特定则 (3), 使得 \(J\) 最大
    • 原子实贯穿和极化
习题
  • 计算线系的能量和跃迁的波长
    • 比如已知 \(Z = 45\) 的铑的电子组态 \(1s^2 2s^2 2p^6 3s^2 3p^6 3d^{10} 4s^2 4p^6 4d^8 5s^1\),
      • 计算基态频谱:
        1. 拿到 \(Z\) 可以排电子组态 (electron-shell-of-z Z): 
          (electron-shell-of-z 45)

          (((1 . S) . 2) ((2 . P) . 6) ((2 . S) . 2) ((3 . D) . 10) ((3 . P) . 6) ((3 . S) . 2) ((4 . D) . 7) ((4 . P) . 6) ((4 . S) . 2) ((5 . S) . 2))

          Note: 啊, 上面的程序好像是错的… 不过因为没有时间所以就这样吧, 保留的原因是为了说明程序是有错误的, 不删掉的原因是因为懒. (一个简单的猜想是填的时候要么是不满足轨道的选择 electron-shell-next, 要么是我那块的代码写岔了.)

        2. 对于排满的轨道就不考虑了, 直接考虑没有排满的轨道. 对于题目给的, 没有排满的轨道为 \(4d^8 5s^1\), 于是由洪特定则, 将 \(S\) 和 \(L\) 填最大未满 (\(s = \frac{3}{2}, l = 3\)), 得到 \(j = l+s = \frac{9}{2}\), 于是最终的原子态 \(^4F_{9/2}\).

多原子分子

X 射线和激光

X 射线

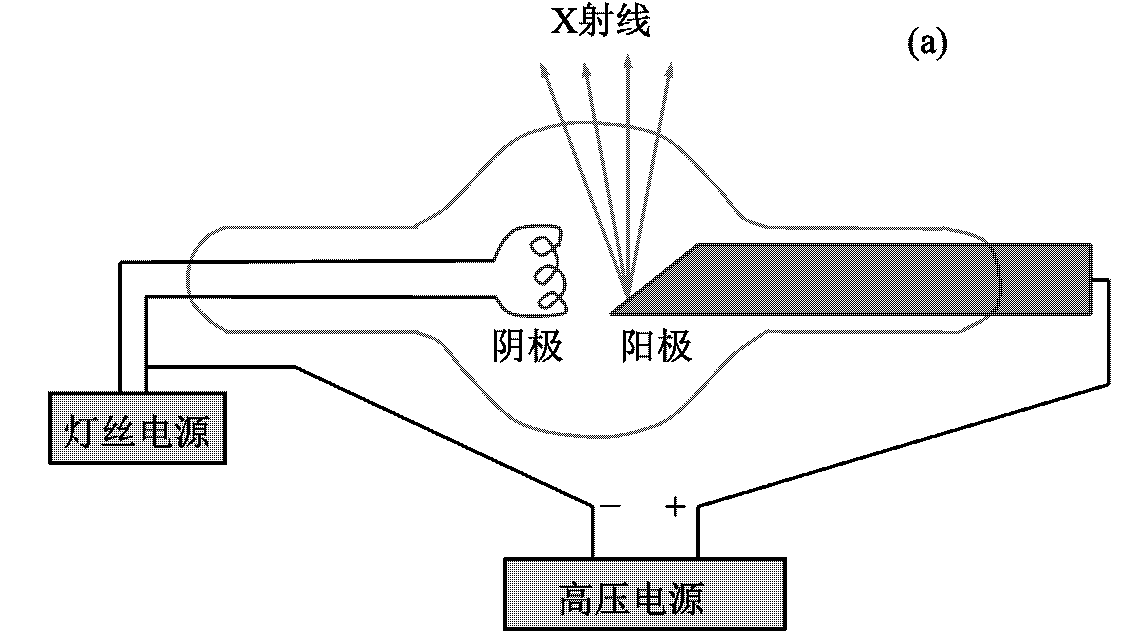
  • X 射线的 产生

    X 射线管: 高能电子打击靶物质 (电子束, 靶物质, X 射线):

    /_img/pieces/atomic-physics/x-ray.png

    或者通过同步辐射的方式来产生, 对比之下可调范围更广:

    X 射线 发射谱:

    • 对于 X 光管, 通常:

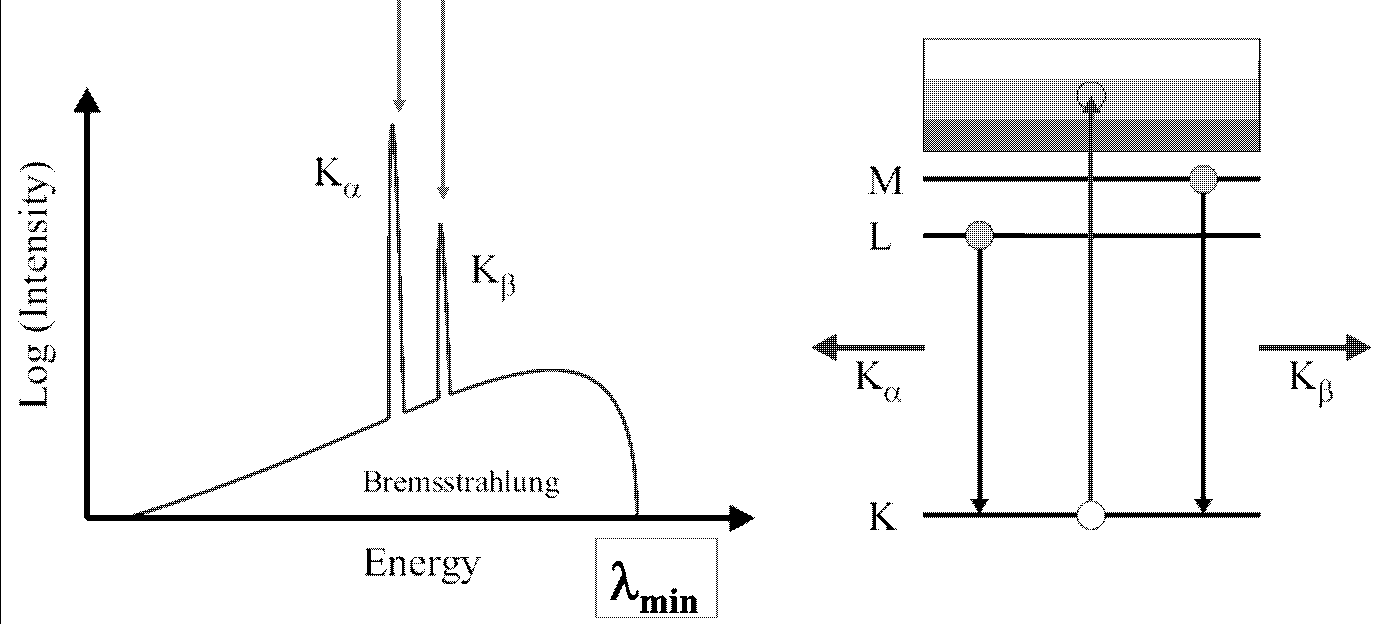
      /_img/pieces/atomic-physics/x-ray-spem.png

    • 对于连续谱 (韧致辐射, 变速运动产生)
  • X 射线的 实验
    • 偏振: 石墨双散射
    • 衍射:

      劳厄晶体衍射和晶体结构测量 (布拉格 \(2 d sin α = n λ\))

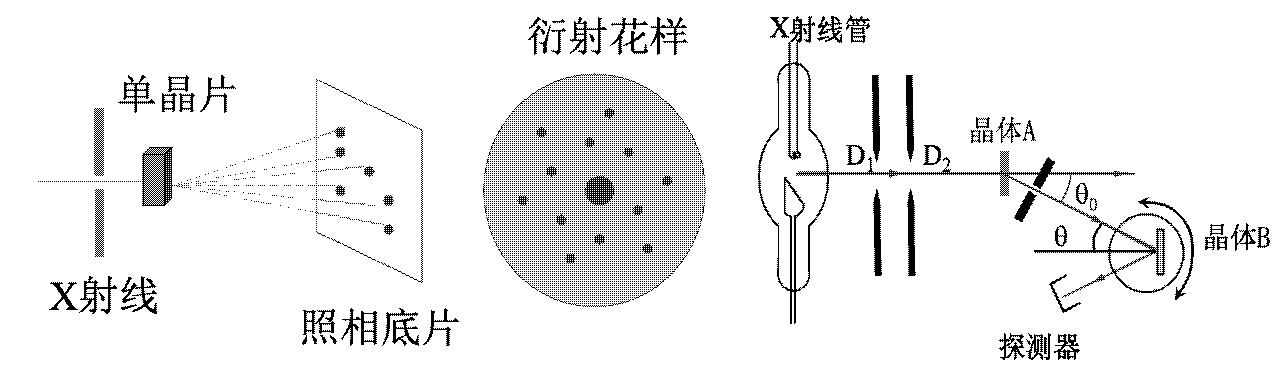
      /_img/pieces/atomic-physics/x-ray-diffraction.png

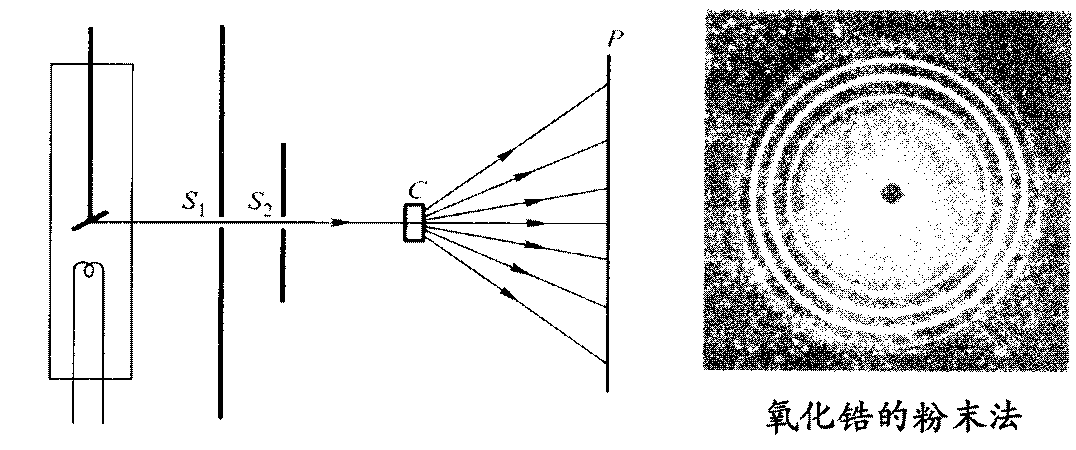
      德拜照相

      /_img/pieces/atomic-physics/x-ray-debye.png

  • X 射线应用
    • DNA 双螺旋
    • 质子荧光分析 \(p-X\): 质子打击样品产生空穴放出 X 射线来分析元素. (和 X 光管结构非常像, 区别在于打击样品的从高速电子变成了质子)

      比如越王勾践剑, 生物样品, 大气污染等 (珍贵的, 大型的, 生物的)

      好处是:

      • 韧致辐射小
      • 探测灵敏度高
      • 可以在大气或者氦气环境下分析
    • 同步辐射
习题
  • X 射线管的工作电压: \(U e = E_{\mathrm{max}} = \frac{h c}{λ_{\mathrm{min}}}\)
  • Moseley 公式: \(ν_{m → n} = R c (Z - 1)^2 (\frac{1}{n^2} - \frac{1}{m^2})\),

    可以用该方法来计算原子序数, 反过来也可以用来计算放出谱线的频率或者壳层的能量.

  • 晶体衍射 (布拉格衍射) \(2 d sin θ = n λ\)
  • 计算吸收屏蔽效果 \(I = I_0 e^{- μ x}\), 其中 \(μ\) 为吸收系数.

激光

原理

认为原子处于两个态 \(E_1, E_2\), 两个态的数量分别为 \(N_1, N_2\) (\(\frac{\mathrm{d} N_1}{\mathrm{d} t} = - \frac{\mathrm{d} N_2}{\mathrm{d} t}\)). 产生激光的三个主要过程:

  • 受激吸收: 吸收光子从低能态跃迁到高能态

    \[\frac{\mathrm{d}N_{12}}{\mathrm{d}t} = B_{12} N_1 u(ν, T)\]

    其中 \(B_{12}\) 为单个原子在单位时间内发生吸收过程的概率. \(B_{21} = B_{12}\)

  • 自发辐射: 从高能态跃迁到低能态发光

    \[E_2 → E_1: - \frac{\mathrm{d} N_2}{\mathrm{d} t} = A_{21} N_2\]

    其中 \(A_{21}\) 称为爱因斯坦自发发射系数, 为单个原子在单位时间内发生自发辐射的概率.

  • 受激辐射: 激发到高能态跃迁到低能态

    \[E_2 → E_1: \frac{\mathrm{d} N_{21}}{\mathrm{d}t} = B_{21} N_2 u(∨, T)\]

    其中 \(B_{21}\) 为单个原子单位时间内受激发辐射概率, \(u(ν, T)\) 为辐射场密度. 受激辐射光与外来光的频率, 偏振方向, 相位及传播方向均相同 (全同光子) 的相干光, 有光放大作用.

  • 谐振腔选频

其他激光器原理

  • X 射线自由电子激光器

    高速电子在不均匀磁场中运动周期性变速放出辐射.

  • 同步辐射

原子核物理

原子核基本性质

  • 结合能和比结合能

    结合能, 前后质量 (能量) 差, 不过需要注意的是, 计算的时候的质量单位 \(1 u = 931.5 MeV\):

    \[Δ E = (∑_{\mathrm{before}} m - ∑_{\mathrm{after}} m) c^2\]

    比结合能: \(\frac{Δ E}{A}\).

    • 可以用来计算反应放出粒子的运动动量之类的, 需要考虑是否引入相对论修正.
    • 以及类似的有阀能概念 (如果要考虑相对论的话, 需要考虑换系, 否则的话可以用结论 \(Δ E = \frac{M_A + M_B}{M_B}\) (两体碰撞的最大能量).)

    反应 \(Q\) 值 (反应前后粒子质量差)

原子核模型

  • 液滴模型: 能量: 体积, 表面, 库仑, 对称, 奇偶
  • 费米气体模型
  • 壳层模型
  • 集体模型

原子核衰变 (\(α, β, γ\))

  • 半衰期, 衰变

    \[{\mathrm{d}_t N} = N_0 e^{- λ t}, λ = \frac{ln 2}{T_{1/2}}\]

  • \(^4_2α\) 实际上就是 He 核
  • \(β: ^0_{-1}e\) 实际上就是电子
  • \(γ\) 实际上就是光子
  • \(ν\) 中微子

(注: 模型看情况, 不一定适用就是了… )

核能

其他

粒子物理

粒子分类和基本性质

费曼图和定量计算

相互作用统一

宇宙学

这个比较有意思, 多信使天文观测.

End

摆了, 懒得管了, 复习不过来了.