Preface

/_img/lisp/from-linked-list/from-linked-list-to-the-old-yet-modern-computer.png

About this Series

本系列实际上就是在 Basic Emacs for those who are Free 中的 (乱) 翻译的 Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I 的一个个人化的一个阐释和说明. 并且不会仅仅只局限于那篇文章 (指需要缝合进去更多的东西).

嘛, 要是你实在读不下去了, 把这个系列当做是一个营销号来看也可以…

这个更多是用于小组讨论的一个讲稿, 希望这个不会变得太过像是一个学习笔记, 应该去做得多一些.

又: 再叠一个甲, 本人做这个只是业余爱好, 并且里面的东西肯定不是什么非常高深的东西, 基本任何一个寄系同学都可以轻松地发现我这里提到的不过就是寄系课程中早就介绍过的东西, 或者早就已经有非常成熟且完备的理论体系来解决这些问题.

About the Folded Part

在本文中, (以及我其他的大部分博客中) 有许多被折叠起来的部分. 这些部分往往是我觉得有些繁琐, 有些和主体无关, 或者只是单纯地我想要折叠起来. 这些被折叠起来的部分, 我认为大多是可看可不看的. 但是如果恰好你比较闲的话, 请务必看看这些可能很多时候比正文还要长的注记.

一个折叠的例子

实际上我觉得之所以会有这么长的注记, 可能只是因为我废话太多了. 也可能是因为我不太会说话, 导致对类似于 footnote 之类的格式的滥用.

Graphics Styles

关于图标和其他图片的一些说明

这个图标, 实际上和 Lisp Machine, Inc. 的 Logo 是差不多的:

/_img/lisp/from-linked-list/Lisp_Machines_logo.png

(图片来源 Wikipedia)

虽然我也不好说这个没有抄袭的嫌疑… 希望不会被官司催逼. (手动狗头)

并且为了模仿 80 年代的机器的风格, 在本系列中使用的大多数图片, 我都会将其通过 Dither 进行一个风格化的操作. 不过可能 Dither 使用的具体算法可能并不完全一样.

(注: 一个关于 GUI 演化的文章: HOW THE GRAPHICAL USER INTERFACE WAS INVENTED)

(注: 为了能够方便地处理这个 Dither 过程, 所以我写了一个 shell 脚本. 但是因为是我第一次写 shell 脚本, 所以它可能并不是很高明. )

The History and Some Interesting Stories

The 1980s (Old yet Fantasy) Computer

The Old Computers

经常可以看到一些收集 “电子文玩” (也就是一些古董电脑) 的视频, 常常让我有一种 “卧槽, 这也太帅了” 的感觉. 这些古董电脑的设计, 它们的质感都非常的酷. 尽管它们可能并不是那么高效和先进.

/_img/lisp/from-linked-list/Apple_II_typical_configuration_1977.png

(图片来源: Wikipedia (Apple II))

说起 80 年代的上古计算机中, 也许你会觉得它们大多是一些命令行的昏暗程序界面, 比如 Apple II (released June 1977), Commodore 64 (released August 1982), IBM PC (released August 12, 1981) 这样的机器.

(欸, 别说你想到的是什么大型机而不是这些小型的个人电脑… )

实际上 80 年代的电脑也有图形界面的: Apple Lisa (released January 19, 1983) “It is one of the first personal computers to present a graphical user interface (GUI) in a machine aimed at individual business users.”

/_img/lisp/from-linked-list/apple-lisa.png

(图片来源: Mac History: Apple Lisa)

(注: 此处的图形界面不是指能显示图形, 而是指能够使用图形进行一些交互. 毕竟哪怕是 Apple II 也有 一些图形的游戏 嘛. )

虽然 Apple Lisa 在商业上挺失败的 (THE LISA: APPLE'S MOST INFLUENTIAL FAILURE), 但是很好看 (bushi), 但是其口碑貌似还不错. 并且还诞生了 Jobs 的那句著名的话:

Good artists copy, great artists steal.

那么再翻一翻历史, 据说当时 Apple 的开发人员是去了一趟施乐公司 (Xerox) 的 PARC (Palo Alto Research Center) 研究中心, 看到了 GUI 的开发后, 受到了启发, 于是开始开发图形界面.

再找找看历史:

Bolt, Beranek and Newman (BBN) developed its own Lisp machine, named Jericho, which ran a version of Interlisp. It was never marketed. Frustrated, the whole AI group resigned, and were hired mostly by Xerox.

from Wikipedia

(注: 这种时候总是有一种春秋战国时期的感觉, 类似于大公司, 大研究室倒了, 它们放出的人才到了各个地方去继续闪耀. 啊, 要是我也有这种能力就好了. 我记得之前有个创业的大佬来我们学校讲课, 说他从来不写简历, 一旦不想待了, 自然有下家来找他. 羡慕捏… 不过我觉得这样也是 Lisp 衰落的一个原因了, 因为缺乏那种非常强的一个 “中心” 领导. 不过这也导致了其很多的思想, 都被整合进了各种出现的语言里面了. 倒不如说, 不是因为编程语言强大, 而是当时那一堆设计的人比较牛吧. )

那么这个 Lisp Machine 究竟是何方神圣呢? 在了解了什么是 Lisp 之后, 我们可以在之后再慢慢介绍.

Chapter 1: Linked List

A Linked List

任何经过现代计算机系课程数据结构毒打的寄系学生应该都非常了解所谓的链表吧. 所以什么花里胡哨的定义和别的什么, 作为一个无聊的物理系学生, 我便不必班门弄斧了.

那么不妨来一些历史小故事, 在 IBM 704 (1954) 机里面, 有这样的一个内存设置:

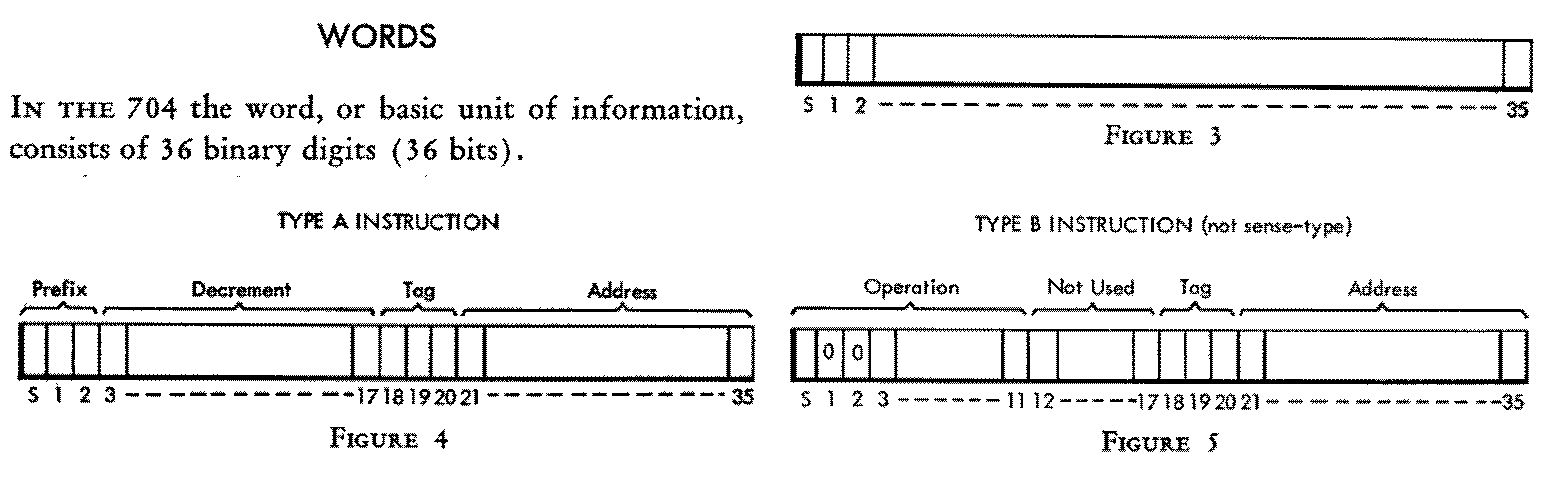
/_img/lisp/from-linked-list/ibm-704-words.png

(图片来源 704 electronic data-processing machine, 一个类似于手册一样的东西. 图片说明: 在 IBM 704 机上的一个 “程序员可见的最小储存单元”, 也就是一个 Word (字, 36 bits), 一个字中可以用两种方式 (Type A/B) 来存放一条指令.)

假设 (实际上也就是差不多这样) 每一个 Word 都有一个对应的地址 (Address) 来访问它, 即如果有一个地址, 那么我们就应当可以通过各种方法定位到这个 Word.

以上, 就是所有的前置知识了. 那么假设你手上已经拥有了这些东西, 那么该如何根据这些东西来构造一个连续有序的数据呢?

(注: 此处所指的连续数据是类似于 1, 2, 3, 4 这样连续有序的一个数据片段. )

如果这个问题对你已经不是一个问题… 请义无反顾地跳过这段说明.

显然, 我们只需要在 TYPE A 的基础上进行一些最简单的魔改即可实现我们的需求. 假定我们现在提供了两种方法可以对 WORDS 进行更加细致的操作:

  • car 可以使得我们去访问上图中的 Address 的部分 (Content of Address Register)
  • cdr 可以使得我们去访问上图中的 Decrement 的部分 (Content of Decrement Register)
  • 并且我们称 cons (CONStructs) 为这样的一个可以被拆成由 car, cdr 数据组合的形式

于是我们便可以如下图所示地构筑起一个链表:

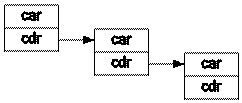
/_img/lisp/from-linked-list/linked-data.png

其中 cdr 中的元素, 要么是一个链表的中止符号 (比如 NIL), 要么是一个链表中下一个元素的地址. 也就是说, 一个链表数据 1, 2, 3, 4, 可以被看作是 cons(1, cons(2, cons(3, cons(4, NIL)))) 的一个形式.

一个小小注记

这里有一个比较 tricky 的事情, 就是明明 car 取得的是 Address 部分的数据, 但是却放着数据, 而 cdr 取得的却是地址.

我不清楚这个该怎么解释呢… 大概是因为寄系的喜欢从低位开始放数据? 但是好像也不是那么回事吧.

根据 Wikipedia: CAR and CDR 里面的介绍, car 和 cdr 的一些 Assembly Macros:

LXD JLOC 4  # C( Decrement of JLOC ) → C( C )  # Loads the Decrement of location JLOC into Index Register C
CLA 0,4     # C( 0 - C( C ) ) → C( AC )        # The AC register receives the start address of the list
PAX 0,4     # C( Address of AC ) → C( C )      # Loads the Address of AC into Index Register C
PXD 0,4     # C( C ) → C( Decrement of AC )    # Clears AC and loads Index Register C into the Decrement of AC

上面的是对于 car(J) 的一个具体的代码, 然后对于 cdr, 则是

LXD JLOC 4  # C( Decrement of JLOC ) → C( C )  # Loads the Decrement of location JLOC into Index Register C
CLA 0,4     # C( 0 - C( C ) ) → C( AC )        # The AC register receives the start address of the list
PDX 0,4     # C( Decrement of AC ) → C( C )    # Loads the Decrement of AC into Index Register C
PXD 0,4     # C( C ) → C( Decrement of AC )    # Clears AC and loads Index Register C into the Decrement of AC

虽然不能够解释为什么会有 car 和 cdr 名字和意义的小小冲突, 但是在考据的时候我觉得很快乐. 我觉得这才是搞搞历史的快乐, 虽然现在我并没有找到关于当时设计者的回忆和说明之类的东西, 这让我感到有一些不满.

关于这种当事者的回忆性质的文章的一个补注

之所以我提到了这类回忆性质的文章, 是因为我看到了一篇类似于回忆录一样的文章: Macsyma: A personal history. 里面对于 Macsyma 的化简算法有一个比较有趣的回忆, 如果未来有时间的话, 我想仔细阅读一下更加细致的一些历史.

并且关于这些历史, 我觉得除了好玩之外, 实际上还是很让人了解为啥这些大佬会想到这些的原因, 比如上文所述的一个故事:

Actually Minsky was unwilling to supervise another thesis in integration. He wanted his students to work on new applications of artificial intelligence, rather than improve old ones. My initial work thus was on proving that integration was undecidable. I heard of the recent result by a Russian mathematician that proved the undecidability of Hilbert’s tenth problem on polynomials with integer coefficients (Matiyasevich, 1993). I believed that this result could be extended to integration problems in the calculus. After making significant progress on this problem I found out that Daniel Richardson had recently followed the same approach and proved the theorem, although he relied on the absolute value function toward the end of the proof, a step that made the proof somewhat controversial (Richardson, 1968). Thus, in 1965 I was able to get Minsky to agree to my original goal.

(注: (一个大意介绍) Minsky 是作者的老师 (?). 但是作者在听说 Hilbert 问题被解决之后, 于是认为就有了可以解决该问题的方法了. 不过这个时候真是让人羡慕.)

但是最近比较忙, 还需要做 pre 和从零开始搓代码, 所以先这样吧. DDL 真的是万恶啊…

当然, 实际上也并不一定需要让 cons(val, addr) 来进行构建一个链表, 比如在一个 WORD 里面高低两位都存着值 cons(val1, val2) 也不是不行.

Expression of Linked List

显然, 我们不会真的使用 cons(1, cons(2, cons(3, NIL))) 这样的形式去表示一个链表, 就像在任何一个数学系统中都会引入的一个操作: 使用一系列简单的注记符号:

  • 记 cons(val1, val2) 为 (val1 . val2)
  • 显然, 一个链表将会被记作 (1 . (2 . (3 . NIL))), 而为了更加简便, 引入 (1 2 3) 来表示一个链表.
  • 显然, 这样的记号系统是极其简单的, 对于一个程序也是非常容易处理的, 比如我们可以如下构建一个简单的 Parser 来从一段文本中读取一个链表: 
    ELEMENT     = LINKED_LIST | ATOM;
LINKED_LIST = '(' (ELEMENT)* ')';

    其中, 使用 ATOM 来表示一个不是链表的元素, 比如 1, 2, any-thing, so-so 之类的几乎任何的东西.

    关于这个的一些注记

    显然, 上面的文法是不完备的, 哪怕是想要做一个更加简单的例子, 也需要一些稍微 “复杂” 一些的处理.

    假如以 JavaScript 为例, 或者你也可以将其写成一个 Python 程序, 或者也可以写成 C 语言程序之类的.

    /* Some enhancement for JavaScript String.scan() */
String.prototype.scan = function (regex) {
  if (!regex.global) throw "Scan Error";
  var self = this;
  var match, occurrences = [];
  while (match = regex.exec(self)) {
    match.shift();
    occurrences.push(match[0]);
  }
  return occurrences;
};

var strict_mode = false;        // if throw when enter parse error
var dbg = true;
var DBG_WARN = 1;
var DBG_ALL = 0
var dbg_level = DBG_WARN;

function dbg_log(message, level = 0) {
    if (dbg && level >= dbg_level) { console.log(message) }
}

function cons(car, cdr) {
    cdr.unshift(car);
    return cdr;
}

function read(input) {
    let tokens = tokenrize(input); // tokenrize the input
    return parse_element(tokens);
}

function tokenrize(input) {
    let token = /(\(|\)|\.|[^\s\(\)]+)/g; // Note: token regexp need to be better
    return input.scan(token);
}

function parse_element(tokens) {
    dbg_log('element: [' + tokens.join(', ') + ']');

    let result;
    let first = tokens[0];

    if (first == '(') {
        tokens.shift();
        result = parse_linked_list(tokens);
    } else {
        result = parse_atom(tokens);
    }

    dbg_log('element returned ' + result);

    return result;
}

function parse_atom(tokens) {
    dbg_log('atom: [' + tokens.join(', ') + ']');

    let first = tokens.shift();
    if (first == ')') {
        if (strict_mode) {
            throw "Unmatched ')'. ";
        } else {
            dbg_log("Parse ATOM: Unmatched ')', returned NIL.");
            return NIL;
        }
    } else {
        dbg_log('atom returned ' + first);
        return first
    }
}

function parse_linked_list(tokens) {
    dbg_log('linked_list: [' + tokens.join(', ') + ']');

    let elem = tokens[0];
    let result;

    if (elem == ')') {
        tokens.shift();
        result = [];            // NIL
    } else if (elem) {
        elem = parse_element(tokens);
        result = cons(elem, parse_linked_list(tokens));
    } else if (strict_mode) {   // when empty tokens
        throw "Unmatched ')'"
    } else {
        dbg_log("Unmatched ')', try to recover... ", DBG_WARN);
        result = []             // NIL
    }

    dbg_log('linked_list: [' + result.join(', ') + ']');
    return result;
}

function format(elem) {
    return typeof elem === 'string' ? elem : '(' + elem.map(format).join(' ') + ')';
}

    注: 上面的程序其实还是有 (亿) 点问题的 (无奖竞猜: 那么是什么问题呢? 这下网安的同学应该就会有话要说了, 并且这里有好多问题, 有功能逻辑上的一些无伤大雅的, 还有一些致命的会引发大危机的, 没错, 不是我太菜, 而是我故意留的 bushi, 我在上面的代码里面修改了错误, 但是并没有在下面的例子里面更新错误, 打逆向的同学可以考虑试试, 不过我猜应该没啥问题. ).

    但是限于我能力有限, 并且对 JS 不太熟练, 不太能够处理得更好… 并且这个程序非常得不通用, 不过我会在最后重新实现一个更加漂亮的程序, 来作为一个更加合理的结束.

    不过现在如果你想试试看的话…

    Click Me to Try The Program

    RESULT:

    (不过请忽略这个丑陋的交互界面, 我想要之后修改一下博客, 让它能够添加类似于可交互的代码块… 不过这个是后话了. )

    不过除了像上面 JS 这样自顶向下递归地构建解析器, 你也可以通过维护一个栈来表示上面的代码的层级… 然后自底向上地去构建一个 Parser:

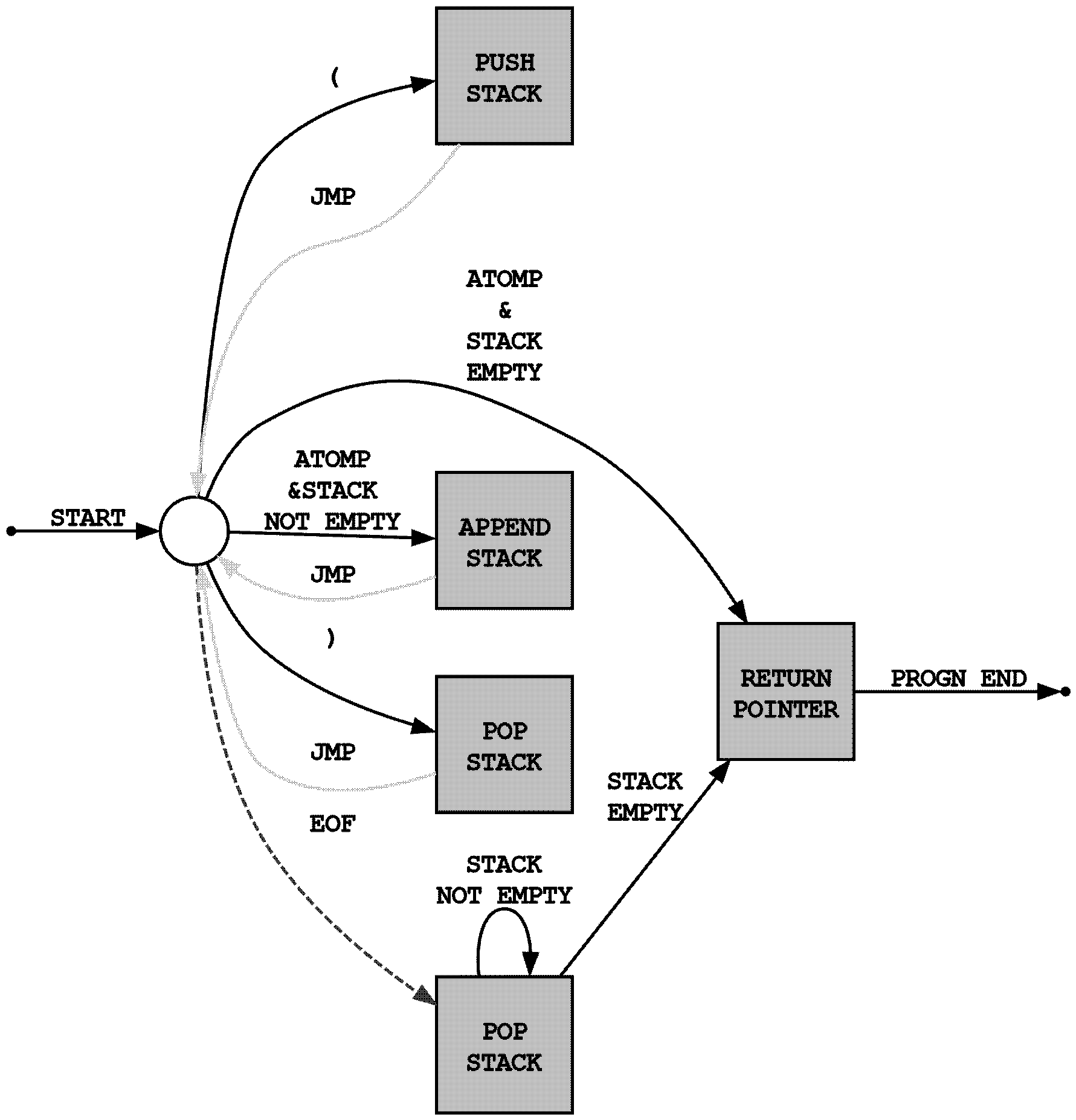
    /_img/lisp/from-linked-list/turing-machine-buttom-up.png

    关于 Parser, 文法, 语法, 词法, 句法…

    实际上我可能是到现在突然有了那么点对词法, 语法, 文法的理解. 以及如何去比较实在地去处理它们. (结果仔细一对比讲义, 发现理解得一塌糊涂.) 我将会用我自己的理解来进行解释.

    在一般的语言里面, 一个单词由一些简单的规则来进行组成. 比如用表音符号表示音节然后组成单词 (一个最恶心我的就是日语片假名对洋文的音译), 比如使用词根来进行组成 (但是我还真不记得几个词根了) 等等.

    在上面的 tokenrize 方法中, 实际上就是将输入的连续字串, 通过 scan 方法来切割成一段段的单词有序链表. 而我认为词法就是告诉 tokenrize 如何去切割单词的一个方法. (也就是上面的那个正则表达式)

    一个更加无聊的例子就是 Toki Pona, 一种人造语言. 其单词仅有 120 个, 所以你大可以穷举历遍的方式来进行单词匹配, 即若当前读到的单词部分在字典里面, 那么就认为这是一个合法的单词:

    (defun scan (sequence)
  (let ((word (read-word-from sequence)))
    (if (find word toki-pona-dictionary)
        (cons word (scan (rest-of sequence)))
        NIL)))

    (显然上面的方法并不是一个很好的算法, 但是大意是这样差不多了. 你可以在这个文档里面 (A Formal Grammar for Toki Pona) 找到一个对其的上下文无关的语法定义. 并且可以发现其中就是用穷举的方式进行单词匹配的. )

    但是如果这个词法并不是一个可以穷举的有限集合, 比如在编程里面的变量名 (原则上来说是无穷的, 实际上来说是有限的). 比如在大部分语言里面, 一个好的变量名往往通过下划线分割, 不能够以数字开头, 也就是满足如下差不多的一个正则规则:

    VAR_NAME = [a-z] [a-z0-9_]*;

    显然, 我们可以根据这个正则规则去 构造一个自动机去正则匹配, 并且假如我们现在想要拓展新的规则, 比如说要有一个类名称, 需要用大写字母开头 (比如 Ruby 里面的类的定义, 虽然下面的不完全是就是了):

    CLASS_NAME = [A-Z] [a-zA-Z0-9_]*;

    于是只需要通过 TOKEN = VAR_NAME | CLASS_NAME 这样的或操作, 即可拓展原有的正则表达式, 使其成为一个新的正则表达式, 于是可以用来进行匹配.

    而文法, 比如说是一般语言里面的 SVO (主谓宾) 结构 (实际上是狭义的 “句法” ?), 实际上在我看来, 就是在词的基础上的结构匹配, 也就是描述一个词在句子中是如何组织的. 比如:

    SENTENCE = SUBJECT VERB OBJECT
SUBJECT  = NOUN
OBJECT   = NOUN

    (注: 但是实际上这个并不是一个语义完备的定义, 因为可能会出现类似于 HE DRINK COW 这样的虽然满足文法, 但是不太合理的东西. 关于语义检查的部分, 可以在之后进行一个处理. 比如类型检查之类的操作.)

    于是我现在有一种想法, 如果能够通过一定的方式扫描文法中的终结符, 来生成一个用于 tokenrize 的正则表达式. 比如将上面的例子进行一个拓展:

    ELEMENT        = LIST
               | ATOM;
ELEMENTS       = ELEMENT
               | ELEMENT ELEMENTS;
LIST           = '(' ')'                # empty LIST
               | '(' ELEMENTS ')';
ATOM           = STRING
               | SYMBOL;
           
@terminals                              # the following is terminals
SYMBOL         = ANY_CHARS;
STRING         = '""'                   # empty STRING
               | '"' STRING_ESCAPES '"';
STRING_ESCAPE  = ANY_CHAR
               | '\"';
STRING_ESCAPES = STRING_ESCAPE
               | STRING_ESCAPE STRING_ESCAPES;
ANY_CHAR       = 'a' | 'b' | 'c' | 'd' | # ...;
ANY_CHARS      = ANY_CHAR
               | ANY_CHAR ANY_CHARS;

    对于 terminal (终结符) 以及用 ='…'= 包围的元素, 应当被识别并作为正则表达式用或进行构建. 比如说, 上面的例子应当被构建为: ='(' | ')' | STRING | SYMBOL= 类似这样的一个正则表达式.

    假设将上面的正则表达式作为一个 scan 规则进行去扫描, 那么就可以将结果扫描出来得到一个 tokenrize 之后的符号串. 然后在这个新的符号串里面, 就可以去进行继续的 parse…

    关于 parse 的话, 上面的递归方式 (自上而下) 和栈 (自下而上) 的方式, 稍微发展一下的话, 就会有 LL 和 LR 等 parser 了.

    嗯, 首先我申明一下, 我只是旁听了一段时间的编译原理, 并没有很会这个编译原理. 嗯, 再叠一个甲, 我对我说的这个语言学也是一窍不通, 只是在查资料的时候发现了这些概念并且觉得这些概念非常好玩而已. 至于最开始搞工程的那帮大佬是否了解语言学, 以及他们设计的时候在思考什么, 我可能需要更多的一些查询.

    • The Beginnings of FORTRAN (Complete) 关于 FORTRAN 的一个回忆性质的记录片, 其中提到了 FORTRAN 作为当时最早的一个可编译的语言:

      None of this theory existed. Nothing was known about parsing. It was all invented at the time and it's not a case of choosing between this method and that method, and this theory and that theory. There were no theories.

      They have been able to think top down and bottom up. (8:48)

    • Plankalkül a high level language from the 1940s by Eric Lefevre Ardant 实际上最早的 (设计) 是一个叫做 Plankalkül 的编程语言 (在一台叫做 Z1 的机械计算机上). (不过并不完整, 更多应该是一种设计. 完整的实现要等到很多年以后了… )

      Plankalkül was more comprehensively published[vague] in 1972. The first compiler was implemented by Joachim Hohmann in his 1975 dissertation.

      (更多关于 Plankalkül 的文档, 可以参考一下 Plankalkül, Bram Bruines 的一个文档)

    • 更多的参考
      • Early programming languages (Stanford 的一个 PPT ?)

        其中的首图为 Mother Tongues, 一个更加清晰的版本如下:

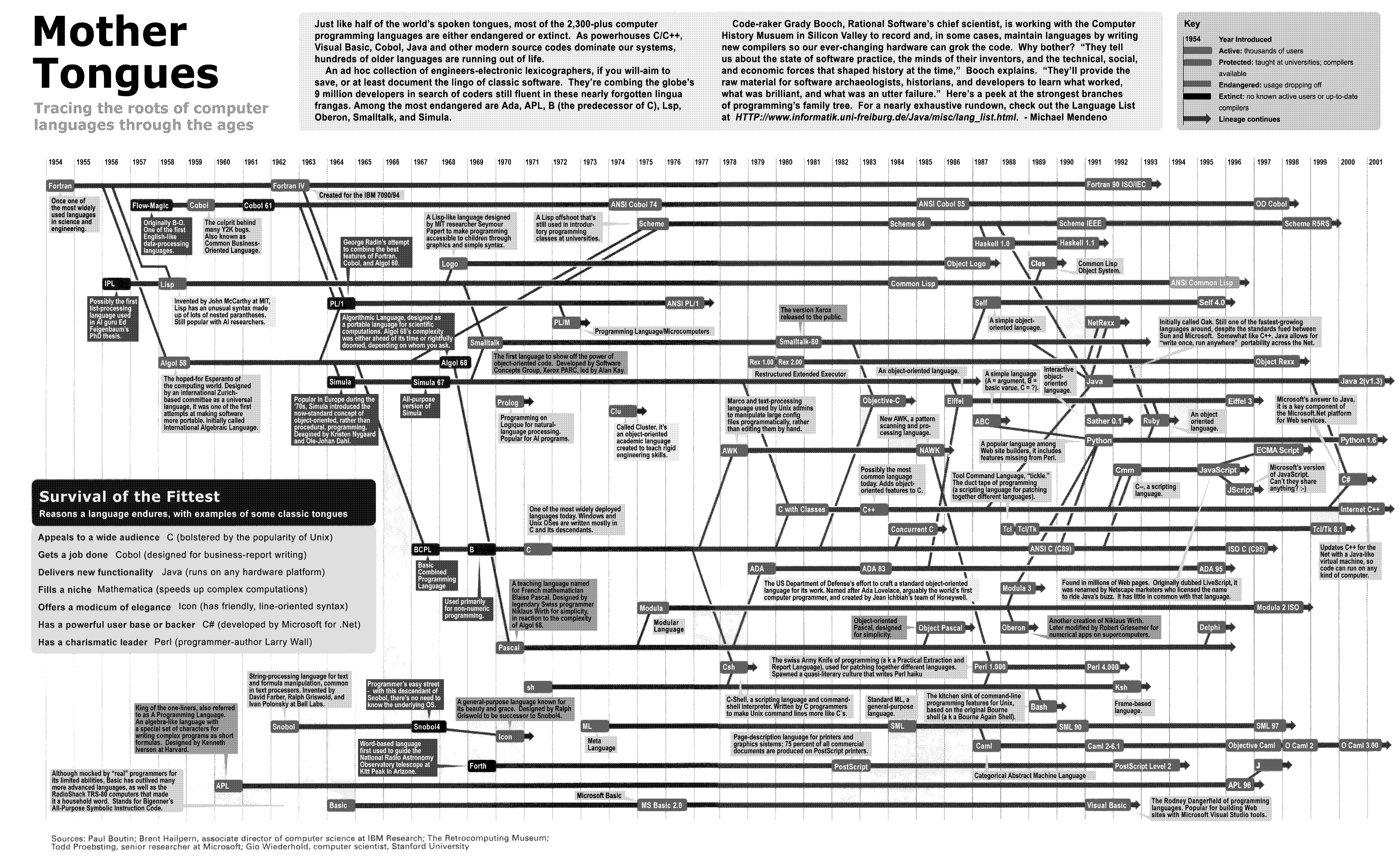
        /_img/lisp/from-linked-list/mother-tongues.png

        (原图来源于 网络 实际上是从一个 R 语言教程里面偷来的)

那么现在我们便可以 literally 表示一个线性的链表结构. 并且既然有了数据结构, 那么就需要有对数据结构的操作和处理的函数. 显然, 我们已经引入了三个基本的函数 (下面只是最定性的定义):

  • cons(a, b) 将两个东西合在一起
  • car(con) 得到合在一起的前一部分
  • cdr(con) 得到合在一起的剩下的部分

那么在这三个函数基础上, 我们不妨再多要一些函数:

  • eq(atom1, atom2) 将两个 ATOM 进行判断, 如果相等就返回 T, 否则为 F
  • cond(p1 -> exp1, p2 -> exp2, ..., T -> exp) 为条件分支语句, 假如条件谓词 p1 为真, 则返回得到 exp1, 以此类推.
  • atom(elem) 判断一个 elem 是否是 ATOM, 显然, 若不是, 则为 LIST, 因为在当前的符号系统中, 我们有且仅有两种元素: ATOM 和 LIST.

我们假定这五个函数是一个天然具有的函数, (并且实际上这五个函数并不难实现, 不论是从什么角度上来看都是这样的 (大概)). 那么我们理论上就拥有了一个与机器无关的, “天然” 存在的像是 “公理” 一样的存在.

([2023-06-20] 勘误: 丈育了, 数数都不会数了, 上面的那是五个吗? 分明是六个.)

并且在之后会看到, 这几个 “公理” 一样的函数, 可以通过巧妙地组合, 构建出一系列丰富的函数, 甚至在其基础上, 可以构建出一个华丽的计算系统.

为了不违背广告法

我觉得大部分的数学书都有一种违背广告法的嫌疑, 因为它们往往都会在书中加入一些夸大其词的说法, 比如: “易证”, “显然”, “容易得到” 这样的话. 尽管对于作者, 或者作者抄的原书的作者来说, 这些证明可能是极其 trivial 的.

(并且往往还有这样的一个笑话: 两个数学系学生见面谈论问题, 甲说了一个非常简单的问题, 在几个小时之后, 乙同学终于高兴地说道, 哦, 这真是一个简单的问题.)

这里不妨做一个小小的妥协, 毕竟脱离了实际的机器实现, 谈论具体的操作, 好像确实有点不太对劲… 但是如果要拿 IBM 704 机来说事, 一来我不会, 二来我觉着我也不太能够搞到一台 IBM 704 机…

不过我找到了一个古董文档 Writing and Debugging Program – Memo 6, 里面虽然很难辨认, 但是列出了一些函数对应的汇编指令代码. 如果感兴趣的话, 可以试试. 虽然我没有看过就是了

(这已经非常仁至义尽了吧 bushi)

(如果有时间, 我觉得可以试试看糊一个 demo. )

(注: 我希望在之后可以用 LLVM 来构建, 就像是 Clasp 干的事情一样, 用 LLVM 对 Common Lisp 进行编译. 可以参考这个演讲 2018 LLVM Developers’ Meeting: C. Schafmeister “Lessons Learned Implementing Common Lisp with LLVM”)

Chapter 2: All the Laws

那么假设现在已经拥有了这样的干净的几个函数, 我们不妨把各种肮脏的繁琐的细节丢掉, 接下来就是一些比较漂亮的构筑过程和结论了.

(注: 这一章我觉得可以写得很长, 也可以写得很短. 可是如果写得太长了, 就会不得不把下一章的内容给剧透了; 如果写得太短了, 就不知道为啥要这样构造了.)

为了不会出现像数学书里面的那种该死的 “首先你需要知道, 然后你为了知道这个首先你需要知道, 你需要知道… ” 这样的像是 RPG 游戏一样的无聊的情节…

这里剧透一下第 3 章: Lambda Calculus. 不过在这里我不会剧透第 3 章里面要讲啥. (嘿嘿, 任君猜测咯) 假如你点击了上面的链接, 发现我还没写好 跑路了, 你也可以点击这个链接: [[/reading/calculi-of-lambda-conversion/][[Reading] The Calculi of Lambda Conversion]], 来看看我之前做的一个笔记 虽然那个最后也跑路了.

假如你没接受过计科导图灵机的折磨

/_img/lisp/from-linked-list/turing-machine.png

(图片来源 Computing: From Turing to today)

那么首先恭喜你, 其次请你看看这个 Make A Turing Machine Yourself 中对图灵机的介绍. 或者可以看看下面这个省流版本:

通过规则储存的匹配的规则和状态转移和读写规则实现的计算模型, 我认为就是一种图灵机.

(defparameter turing-machine-rule
  '((STATE-1 . ((MATCH-RULE-1 . WRITE-MOVE-RULE-1)
                (MATCH-RULE-2 . WRITE-MOVE-RULE-2)))
    (STATE-2 . ((MATCH-RULE-3 . WRITE-MOVE-RULE-3)))
    ...))

(defun turing-machine-stepper (reader-head rule state)
  (let* ((patterns (assoc state rule))
         (readed   (read-from reader-head))
         (matched  (find-if (pattern-match readed) patterns
                            :keys #'match-rule)))
    (if matched
        (turing-machine-stepper (move-by matched reader-head)
                                rule
                                (next-state matched)))))

不过放心, 这个只能算是一个伪代码而已. 并且哪怕你一点也不了解图灵机, 那么也没有问题, 来看看下面的一个东西吧:

而和状态和规则所不一样的一个思路则是一种函数的观点. 事实上, 如果用一个比较数学的说法来说, 函数, 也就是映射 (Map), 可以被定义为一个二元关系, (唯一稍微严格一些的要求是这里二元关系对于一个变元 \(x\), 也就是 \(x ∈ \mathrm{dom} f = X\), 有其只有一个元素与之对应 \(f(x_1) = y_1 ∧ f(x_2) = y_2 ⇒ y_1 = y_2\)).

于是对于一个有限集合, 显然可以通过穷举的形式来进行表述这样的映射关系:

\[f: \left\{\begin{matrix} x_1 & \mapsto & y_1 \\ & \cdots & \\ x_{n} & \mapsto & y_{n} \end{matrix}\right.\]

那如果是一个无限的 (可数) 集合呢, 那么总可以构造数学归纳法进行递归地描述, 那么如果是一个无限的不可数集合呢? 欸嘿, 不清楚, 这我还真没查过.

(一个普通的想法是可能可以通过分类的方式来对这样不可数的无穷集合来进行映射, 比如对于一个 Heaviside Step Function: \(H(x) : \left\{ 0 < x \mapsto 0, x = 0 \mapsto \frac{1}{2}, 0 < x \mapsto 1 \right\}\), 但是这样问题又来了, 那么如果这个无穷不可数的集合又恰好不可比较呢? 那就去找一些可以比较的方式吗? 嗯, 如果真的有时间的话, 我会去找找相关的资料的.)

对于寄系的同学, 也许会说, 哦, 你真傻, 计算机可是有表示极限的, 所以没有无穷的精度之类的; 而对于物理系的同学, 可能会说: 差不多得了, 这数能测吗? 能测的话, 不确定度多少? 误差多少. (或者是你这玩意能微扰吗? 能展开吗? bushi)

那么现在在函数的视角里面的计算是什么呢? 我个人认为是一种匹配和替换. 比如以一个垃圾求导程序为例:

(defun window-map (func lst)
  (loop for elem in lst
        for count from 0
        collect (apply func (append (subseq lst 0 count)
                                    (nthcdr (1+ count) lst)))))

(defun diff (exp var)
  (cond ((constp exp) 0)
        ((addp   exp) (apply #'+          ; (f + g)' = f' + g'
                             (mapcar #'diff (rest exp))))
        ((mulp   exp) (apply #'+          ; (f * g)' = f' * g + f * g'
                             (mapcar #'*
                                     (window-map #* (rest exp))
                                     (mapcdr #'diff (rest exp)))))
        ((sinp   exp) (* (cos (rest exp)) ; sin(X) :-> cos(X) * X'
                         (diff (second exp))))
        ((expp   exp) (* exp              ; exp(X) :-> exp(X) * X'
                         (diff (second exp))))))

(注: 之所以说这个是一个垃圾求导, 是因为这样写的话, 程序就写死了, 不过至少能够表现一个 cond 进行分类的一个感觉, 所以保留了这个例子. 虽然更多的理由是我真的需要写这样类似的一个程序… 关于如何构建一个可以拓展的求导程序, 我认为可以在之后去介绍 (bushi).)

啊, 发现自己好像扯得有些远了, 那么回过来一下吧. 在上面的程序中, 或者是上面的编程的做法里面, 有哪些是需要实现的?

  • 模式的匹配和替换
  • 递归地执行和返回
  • (可能还有别的我没有概括到的…)

如果想要满足上面的几个实现的话, 首先就需要的是匹配, 也就是需要将原本简陋的 eq 进行拓展, 然后则是替换和一系列的相关的函数操作.

(我感觉这里我讲的并不是很好…)

Before Construct

众所周知, 高贵的西餐厅需要前菜, 街边的大排档需要凉菜, 所以不管我这篇水文写得如何, 它高低都得来点前戏.

equal

原本的 eq 仅能对 ATOM 进行比较, 那是否可以拓展使其能够进行比较一个复杂的对象呢? 显然是可以实现的:

\[\mathrm{equal}[x,y] := \left\{ \begin{matrix} \mathrm{atom}[x] ∧ \mathrm{atom}[y] & \mapsto & \mathrm{eq}[x,y],\\ ¬\mathrm{atom}[x] ∧ ¬\mathrm{atom}[y] & \mapsto & \mathrm{equal}[\mathrm{car}[x],\mathrm{car}[y]] ∧ \mathrm{equal}[\mathrm{cdr}[x], \mathrm{cdr}[y]]\\ T & \mapsto & F \end{matrix} \right\}\]

(当然, 你也可以写成一个比较长的逻辑表达式: \(\mathrm{equal}[x,y] := [\mathrm{atom}[x] ∧ \mathrm{atom}[y] ∧ \mathrm{eq}[x,y]] ∨ [¬ \mathrm{atom}[x] ∧ ¬ \mathrm{atom}[y] ∧ \mathrm{equal}[\mathrm{car}[x], \mathrm{car}[y]] ∧ \mathrm{equal}[\mathrm{cdr}[x], \mathrm{cdr}[y]]]\))

也许你会有一些疑惑

这个逻辑运算好像不是那五个命令中的一个内容吧, 怕不是超纲了? 实际上并不是, 还是可以通过一些无聊的操作来实现这么一个逻辑运算的:

  • 非 \(¬[p] := \mathrm{cond}[p \mapsto F, T \mapsto T]\)
  • 与 \(∧[p_1, p_2] := \mathrm{cond}[p_1 \mapsto \mathrm{cond}[p_2 \mapsto T, T \mapsto F], T \mapsto F]\)
  • 好了, 接下来就没有任何问题了, 是吧, 逻辑联结词完备集

嗯, 看来这个应该也作为一个前戏欸.

subt (substitute)

既然匹配到了, 那么一个想法就是将匹配到的东西给替换掉. 这里是一个简单的版本: 如何在一个链表结构中替换一个符号?

相信对于读到这里的无聊读者来说, 这应该不是一个问题, 实际上只要对上面的 equal 部分做一些小小的修改 (实际上上面的 equal 就是一个有条件停止的一个递归历遍, 而 subt 也是一个递归历遍):

\[\mathrm{subst}[x, y, z] := \left\{ \begin{matrix} \mathrm{atom}[z] & \mapsto & \mathrm{cond}[\mathrm{eq}[x, z] \mapsto y, T \mapsto z]\\ T & \mapsto & \mathrm{cons}[\mathrm{subst}[x, y, \mathrm{car}[z]], \mathrm{subst}[x, y, \mathrm{cdr}[z]]] \end{matrix} \right\}\]

( 假设我们要用 \(y\) 来替代 \(z\) 中出现的所有的 \(x\). )

一个小小注记

如果你比较闲的话, 实际上会发现可以把这个函数做得更加通用一些:

\[\mathrm{map}[f, z] := \left\{ \begin{matrix} \mathrm{atom}[z] & \mapsto & \mathrm{cond}[\mathrm{eq}[z, NIL], T \mapsto f[z]]\\ T & \mapsto & \mathrm{cons}[\mathrm{map}[f, \mathrm{car}[z]], \mathrm{map}[f, \mathrm{cdr}[z]]] \end{matrix} \right\}\]

而之所以要加上一个 NIL 的条件判断, 是因为 NIL 代表了一个特殊的元素: 链表的终结. 实际上可以糊弄一个简写函数用来表述 NIL 的匹配:

\[\mathrm{null}[z] = \mathrm{atom}[z] ∧ \mathrm{eq}[z, NIL]\]

Others

接下来做的就是一些很麻烦的事情了: 我们可以用链表来表示各种各样的数据, 而这样的数据显然就需要一些对应的操作手法, 对于这些操作手法, 显然需要有对应的函数. 但是这样是否未免有些过于麻烦了呢?

所以我就想啊, 既然马上就要数据结构考试了, 为什么不… 先写这么多然后鸽了

Eval & Apply

这部分我认为就是一个非常绝妙的部分了.

那么为了质量, 我打算留到 S2 部分来进行介绍. (所以如果链接点不开, 那很有可能是我鸽了, 嗯.)

有一种看漫画看到一半结果发现没完结的感觉…