[讲座] 文本数据建模与理解 – 社会计算视角

注

因为时间不够, 所以讲座仅能介绍前一部分, 后半部分的社会计算视角就略去了.

人工智能的两个核心

  • 表示
  • 推理

而其中, 表示是一个非常重要的东西. 因为总所周知, 计算的本质就是信息变换. 而我, 是真的不知道.

或者, 不妨抄一抄 SICP 中对于计算的一段介绍:

计算过程是存在与计算机力的一类抽象事物, 在其演化进程中, 这些过程会去操作一些被称为 数据 的抽象事物, 人们创建出一些称为 程序 的规则模式, 以指导这类过程的进行.

如何算不可算的东西? 或者说, 为了能够让计算机能够计算某类东西, 所需要的一个必不可少的事物是什么 – 那就是 表示.

有了表示, 那么就能够进行后续的 推理 计算. 比如说将一个集合 (群) \(G ∼ Z_m\), 于是就能够用 \(\{0, 1, \cdots, m\}\) 来表示集合元素, 就很容易定义运算 \(+, ×\) 以及 \(G\) 中元素进行运算的方式了. 那么哪怕 \(G\) 里面的元素都是一些阿猫阿狗也没有任何问题了.

同理, 倘若能够给文本一个比较好的表示, 那么就可以根据其为基础进行各种各样的算法了.

文本表示与分析范式

总的一个思路是这样的: 将非结构化的自由文本通过文本分析技术进行编码进行表示, 然后就可以对其进行各种分析, 最后就能够应用到各种各样的领域之中了:

非结构化自由文本 \(→\) 文本分析技术 \(→\) 文本应用技术:

  • 文本分析技术

    分为两个部分: 表示 和 分析:

    • 表示
      • 向量化表示
      • 产生式表示
      • 分布式表示
      • 参数化表示
    • 分析
      • 自然语言处理
      • 自然语言理解
      • 自然语言生成
  • 文本应用技术
    • 社会计算
    • 智能投顾
    • 深度鉴伪
    • 智慧写作
    • 拟人交互

语言模型的演进

第一代: (语言学和统计学的融合)

  • 1916: 通用语言学 从语言学的开始: 语言学
  • 1957: 句法结构 Noam Chomsky
    • Noam Chomsky: 人和动物的区别在于人的语言直接描述递归 (recursion).
    • 图灵机与邱奇: 可计算性和递归, 计算机与人的语言的能力的可相比
    • 并且 Chomsky 还有这样的一个看法: 认为语法是一台处理语言的机器
    • 在编译原理里面也会遇到他, 提出了上下文无关文法, 形式语言这样的高级玩意
  • 1966: 首个自然语言对话程序 ELIZA 诞生
    • 人机对话的神奇现象, 但是实际上是一种 “骗局”, 因为 ELIZA 并没有多么智能
    • 可以试试在 Emacs 里面使用 doctor 命令来体验一下类似的感觉, 效果并不是很惊艳, 只能说只能骗骗愿意上当的人 (bushi)
  • 1971: TF-IDF
    • \(TF-IDF = TF(+, d) × IDF(+)\)
    • 在 Google 的搜索引擎的搭建中也有它的影子, 属于是一种虽然简单, 但是很妙的东西 (具体介绍见下)
  • 1992: N-Gram 模型

第二代: (引入贝叶斯, 分布表示 Distribution Representation, Hidden 模型)

通过引入了隐藏层的概念来进行表示.

  • 2000: PLSA
  • 2003: LDA 模型
    • 引入了 hidden 概念: 隐藏模型, 在当前的 “大模型” 中有表现.
  • 隐马尔可夫模型

第三代: (分布式表示 Distributed Representation, 向语义方向理解)

思路从构建表示, 到自动学习一个表示方式

  • 2003: 神经语言模型
  • 2013: word2vec

第四代: (大模型时代)

  • 2017: Transformer
  • 2018~2022: ChatGPT, BERT
  • ChatGPT: 一个集成了各种功能的东西, 但是不能不承认其在工程上的壮举.

语言模型与 NLP 应用的基础: 文本表示

算法不重要, _表示_ 重要

接下来具体介绍一些关于一些方向的使用:

第一代: 语言学和统计学的融合

  • 向量化表示: 将单词映射到向量空间, 对单次向量进行算术运算.
    • 最朴素的词向量编码: One-Hot. (每一位代表一个单词)

      比如有一列 \(N\) 个单词 ='(happy sad surprised …)=, 那么这个时候就用 ='(1 0 0 …)= 来表示 happy, 用 ='(0 1 0 …)= 来表示 sad. 这样的就是 One-Hot 编码方式.

      (注: 虽然这么说起来听着非常离谱, 毕竟直观来看那有人会这么做呢? 但是实际上还真是这样的, 以之前做的最简单的 “文本识别” 的例子 来看的话, 其中利用一个自动机进行匹配, (if (eq token abbreviation) next break), 那么匹配时就相当于是在一个 Abbreviation 向量空间里面进行比较, 只不过写成这样的向量的形式更加形式化而已. )

    • 词袋模型 Bag-of-Words: 忽略词的顺序, 词频越高, 表示该词在文章中越重要. 数据稀疏维度大, 无法保留词序信息.

      这个有点像是将上面的 \(2^N\) 的向量空间变成了 \(\mathbb{P}^{N}\), 其中 \(\mathbb{P}\) 为频率信息. 这个的感觉和下面的 TF-IDF 很像.

      (map-with-index (lambda (idx word count)
                  `(word ,(update-at idx count (vector-zero))))
                (group-and-count input))
  • N-gram 模型:
    • 保留部分词序, 词频越高表示该词在文章中越重要
    • 比如若 \(N = 1\), 则变成上面的词袋模型
    • 若 \(N = 2\), 则对于一个输入 ='(Hello the lucky me haha)= 就会被拆成 ='(Hello the)=, ='(the lucky)=, ='(lucky me)=, ='(me haha)=. 那么这个时候就相当于是保留了部分的词频信息和词序信息了.
    • 若 \(N = \cdots\), 同理
  • TF-IDF:
    • 上面统计词频的方法有一个比较坑爹的问题: 那就是如果某些无意义的修饰词, 比如 “啊巴巴”, “啊对对对” 频繁地在语境中出现, 那么这些被作为口癖一样的词就会在统计上占据不必要的重要性, 所以要通过一些方法来除去它们的影响.

      (注: 实际上以英文为例, “the”, “a”, “an” 这样的词因为出现得太频繁了, 所以会被认为是 “水词” 而减少影响力. 怎么一股水论文被贬低的感觉)

    • Term Frequency: 词在文档中出现的频次

      (出现多的比较重要)

    • Inverse Document Frequency: 词在文档集的多少个文档的出现的倒序排序

      (去掉出现多的水词)

    • 于是就可以计算一个词的 “重要程度”:

      \[TF-IDF = TF(+, d) × IDF(+)\]

第二代: 分布表示

You shall know a word by the company it keeps!

J.R.Firth. A synopsis of linguistic theory.

在这个时候, 就会有想法去考虑如何在统计的时候加入对上下文的考虑, 因为说话是一个和语境相关的一个东西.

  • 贝叶斯生成模型
    • 词本身 \(→\) 上下文
    • 文章由单词直接表示, 单个词频统计 (词本身)
    • 文章由主题构成, 主题由单词构成: 基于分布假设, 描述词的共现关系 (上下文)

      一个简单的理解 (不一定对): 通过条件概率计算单词 \(w\) 出现在语境 \(c\) 下的概率: \(P(w|c)\). 比如一个语境可以是这个单词周围的一个 \(\{w_i\}\) 单词序列.

  • PLSA (Probabilistic Latent Semantic Analysis 隐藏层)
  • LDA (隐含狄利克雷分布, 据说论文写得很好, 以后试试读读看)

第三代: 分布式语义

这个时候的一个突破的思路是这样的: 通过自监督学习的方式, 来自己给自己找一个可能的表示.

  • 表示学习:
    • word2vec
    • 将 One-hot 的高维稀疏的结果, 变成低维稠密的表示结果 通过计算来得到最终的结果.
    • 自监督学习
    • skip-gram

      是 word2vec 的其中一个实现, 一个比较详细的介绍如下:

      The skip-gram objective function sums the log probabilities of the surrounding $n$ words to the left and right of the target word $w_t$ to produce the following objective:

      \[J_{θ} = \frac{1}{T} ∑^T_{t=1} ∑_{-n \leq j \leq n ≠ 0} \mathrm{log} p(w_{i+j} | w_i)\]

      (Skip-gram Word2Vec)

      论文中使用的方式 (Skip-gram Model):

      • 目标是在 $n$ 维向量空间中表示序列 (word2vec)
      • 数据表示: 有一列由 token (word, 可以认为是最小不可分割元素) 组成的序列, 该序列中的第 $i$ 个 token 为 $w_i$. 其在向量空间中对应 \(\boldsymbol{v}\) 向量. 目标是得到这个向量的表达形式.
      • 考虑该 token 与周围环境的关系:

        \[p(w_{i+j}|w_i) = \frac{\mathrm{exp}((\boldsymbol{v}'_{w_{i+j}})^T v_{w_i})}{∑_{k=1}^w \mathrm{exp}((v'_{w_k})^T v_{w_i})}\]

        即若 $i$ 处为 $w_i$, 则周围 $i+j$ 处出现 $w_{i+j}$ 的概率. 以周围 $c$ 大小的范围作为自己的 scope (认为是可以目力所及的范围), 于是在 $w_i$ 周围的一个序列 $\{w_{i-c}, \cdots, w_{i+c}\}$ 的出现概率: $P(w_{i-c} w_{i-c+1} \cdots w_{i-1} w_{i+1} \cdots w_{i+c} | w_{i}) = ∏ P(w_{i+j}|w_{i})$. 通过对数操作变成求和: $∑ \mathrm{log} P(w_{i+j}|w_i)$.

      • 使得对于序列 $\{w_i\}$ 整体概率最大 (类似极大似然估计) 的 $\{\boldsymbol{v}_i\}$ 即为所需要的表达向量:

        \[\mathrm{argmax} \frac{1}{N} ∑_{i=1}^N ∑_{-c \leq j \leq c, j ≠ 0} \mathrm{log} p(w_{i+j}|w_{i})\]

  • Transformer:
    • Self-attention
    • 输入状态矩阵 - 编码 -> 输出编码矩阵 - 解码 -> 词向量矩阵 * Mask 矩阵
    • 感觉对 Transformer 有了那么点感觉: (个人理解, 不一定对, 以后有时间再详细看吧… )
      • 首先还是整体的模型的框架:

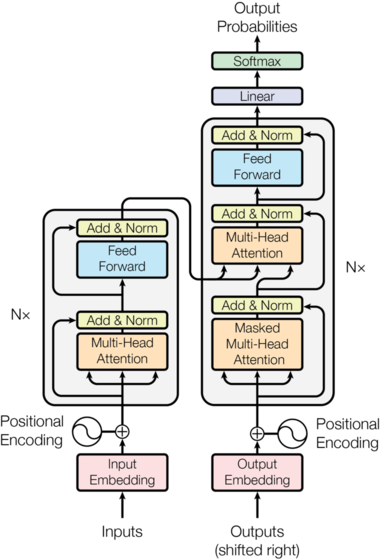
        /_img/lectures/nlp-and-social-calculate/the-annotated-transformer_14_0.png

        (注: 图片和接下来的介绍主要来自 The Annotated Transformer)

      • 这里还是 “表示” 作为核心呢:

        Here, the encoder maps an input sequence of symbol representations \((x_1, …, x_n)\) to a sequence of continuous representations \(\boldsymbol{z} = (z_1, …, z_n)\). Given \(\boldsymbol{z}\), the decoder then generates an output sequence \((y_1, …, y_m)\) of symbols one element at a time.

      • 核心貌似还是一个表示的特征提取…
      • 一个可以参考的 Self-Attention和Transformer

大模型时代:

  • 两阶段预训练模型: 无监督预训练 (pre-training) + 有监督微调 (fine-tuning)
  • 大模型未来趋势
    • 单模态 \(→\) 跨模态
    • 大教堂 \(→\) 大集市
      • Big Science 大科学
    • 数据驱动 \(→\) 数据 + 知识双驱动
    • 记忆大模型 \(→\) 推理小模型
    • 性能模型 \(→\) 可信, 可依赖模型
    • 使用过程不更新参数 \(→\) 基于用户反馈持续学习
    • 学习中融入只是 \(→\) 应用中利用知识

社会计算基本思路

社会计算: 应用的视角.

  • 如何通过文本来帮助解决并计算错综复杂的社会问题

实际上这个给我感觉非常的有意思, 相当于是用文字作为 encoder, 然后通过大语言模型的方式来进行对 encoder 编码的数据重新进行解码, 然后再重新编码输出用于进行更进一步的问题计算和分析.

并且从这个角度来看, 实际上确实 表示 这个部分非常的重要. 只要有了一个好的 encoder 能够将输出的任意的东西编码成一个可计算的数据结构, 那么后面跟着算法去进行推理.

我逐渐理解一切

面向社会计算的 NLP 应用

残念, 该部分没时间去讲了.