Scanning Electron Microscopy

About

参考的资料为 Scanning Electron Microscopy, Ludwig Reimer 的前两章.

The aim of this book is to outline the physics of image formation, electron-specimen interactions, imaging modes, the interpretation of micrographs and the use of quantitative modes in scanning electron microscopy (SEM).

下面默认无标记的都是引用该书的内容. 部分图片有一些标注.

读书的目标在于快速入门并帮助我能设计一个总体的一个光路 🥲.

Overview

一个总体结构的示意图:

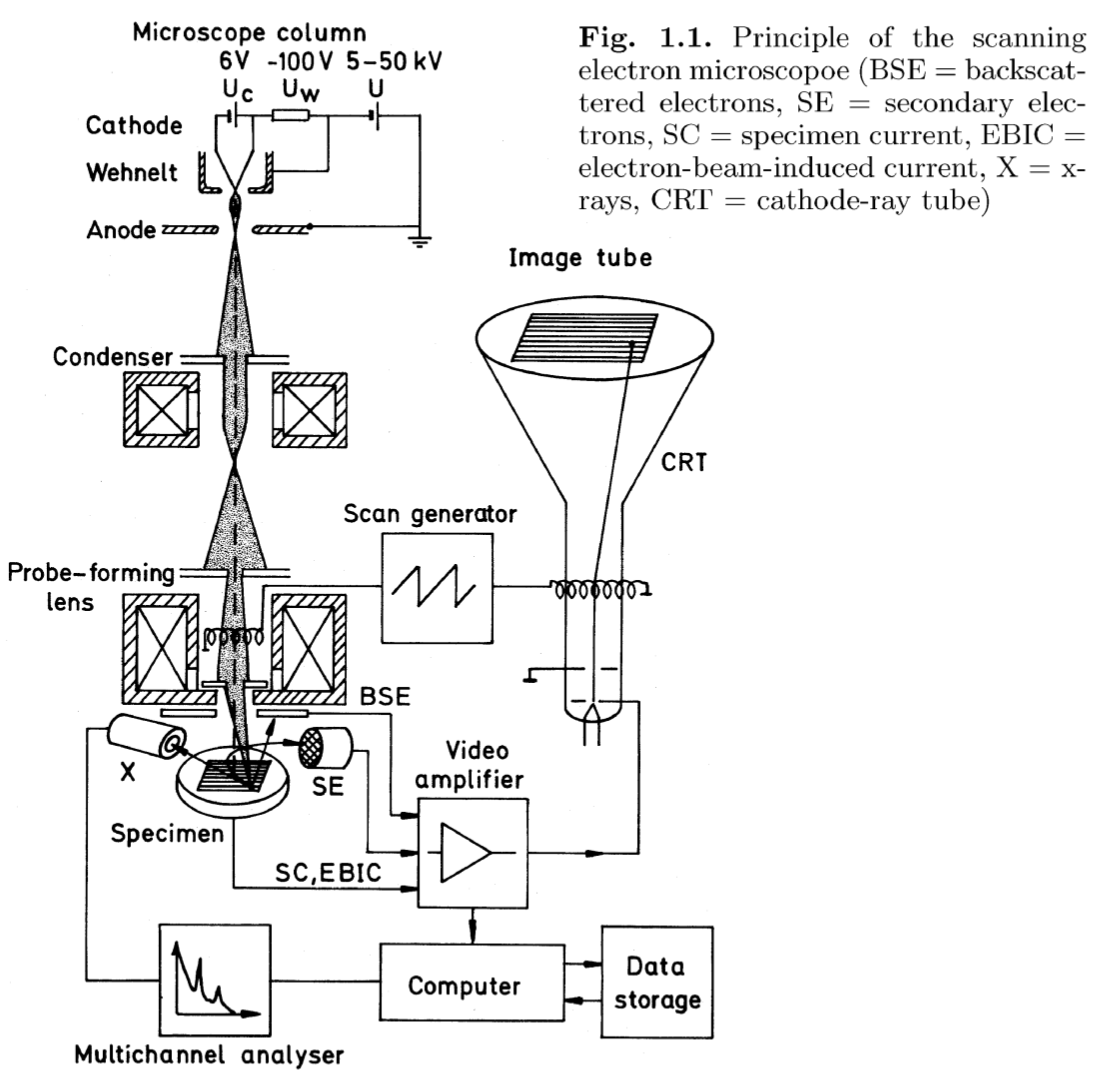
电子枪 Electron Guns

• 阴极 Cathode
  • 阴极 电压 可能的值从 $0.1keV$ 到 $5keV$ (低压 LVSEM), 或者到 $50keV$.
  • 在枪中最小的光束交叉的区域叫做 crossover (交叉斑).

    The smallest beam cross-section at the gun - the crossover.

    其量级对于热发射电子枪 (thermionic emission) 应在 $10 ∼ 50 μ m$ 附近; 对于 Schottky 和场发射 (field-emission) 电子枪, 应在 $10 ∼ 100 nm$ 附近.

  • 经过二到三极透镜系统的聚焦, 探测电子束的宽度 应当在 $1 ∼ 10 nm$, 其在样品表面 照射电流强度 约 $10^{-9} ∼ 10^{-12} A$ 量极.
  • 若需要较高流强 $≅ 10^{-8}A$, 探测电子束的宽度约 $≅ 0.1 μ m$.
• 工作距离 working distance
  • 在探测样本 (specimen) 和最低的 polepiece (极片? ) 的距离为工作距离.
  • 通常的距离约为 数毫米或者数厘米, 根据不同的模式的距离不同.

热发射电子枪 thermionic Electron Guns

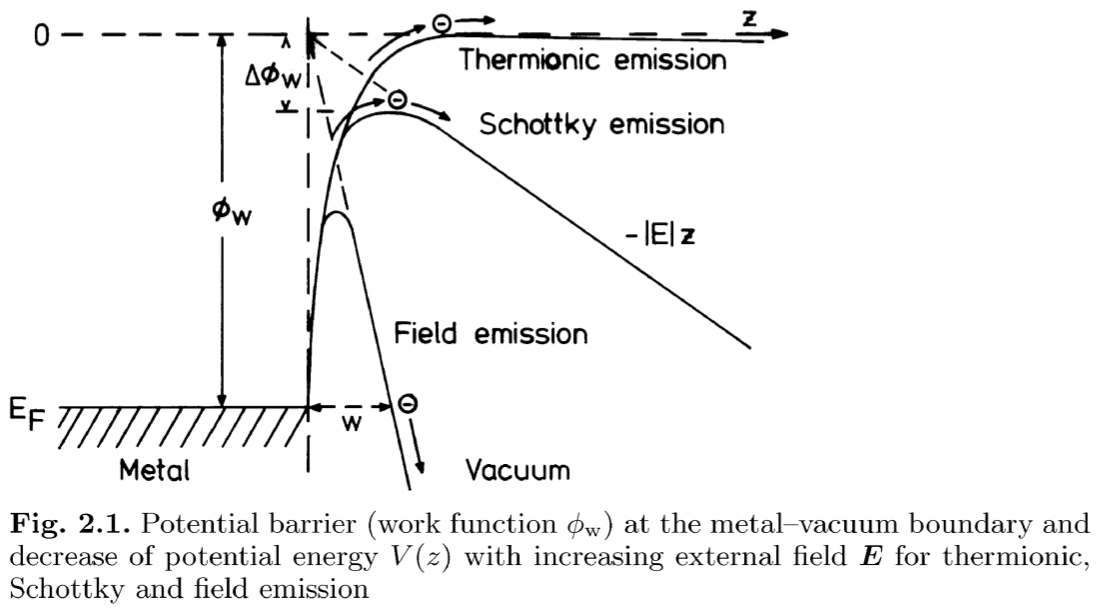
通过加热 (功函数 $φ_w$) 使得电子克复 $E_F$ Fermi 能级的束缚然后被抛出. 在阴极和阳极之间的加速电场 $\boldsymbol{E}$ 提供能量 $V = - |\boldsymbol{E}| z$, 发射的流强 (emission current density) 的 Richardson Law:

$$j_c = A T_c^2 \mathrm{exp}(- φ_w / k T_c)$$

其中 $A$ 为和材料有关的常数; $T_c$ 为阴极尖端的温度; $k$ 为 Boltzmann 常数.

• 工作温度 和 束流密度

  通常为了达到尽可能大的电流, 会使得针尖温度略在电子枪熔点之下 $T_m$

  对于钨 (tungsten, $φ_w = 4.5eV, T_m = 3650K$), 常见的 $T_c = 2500 ∼ 3000 K$. 并且在 $T_c = 2800K$ 时, $j_c ≈ 3 A ⋅ cm^{-2}$;

  对于 Lanthanum hexaboride $\mathrm{LaB}_6, φ_w = 2.7eV$, 工作温度约 $T_c = 1400 ∼ 2000K$, 其电流密度约 $20 ∼ 50 A ⋅ cm^{-2}$.

• 电子枪寿命

  约在 $40 ∼ 200h$ 之间, 取决于阴极材料的蒸发, 在灯丝过细时断裂.

• 工作真空度

  约 $(1 ∼ 5) × 10^{-3}Pa$ 量级的真空度可以防止灯丝氧化. 更高的真空度可以提高寿命, 如在 $10^{-4}Pa$ 下, $\mathrm{LaB}_6$ 可达数千小时. (比如在抽真空的机械泵基础上加上离子泵)

• 加速电压 和 电子物质波波长

  $p^2 c^2 + m_0^2 c^4 = (E + m_0 c^2)^2 ⇒ p = \sqrt{2 m_0 E (1 + \frac{E}{2 E_0})} ⇒ λ = \frac{h}{p}$

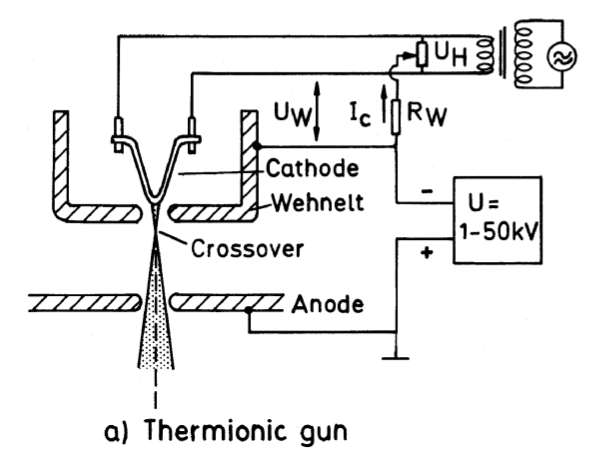
• 栅极 (Wehnelt cup)

  有一个小小的电压降 $U_W = I_c R_W$, 其中 $R_W = 1 ∼ 10 M Ω$, $I_c$ 为最终照射电流 (beam current) 和加热功率 $P_c$ 的关系如下:

  

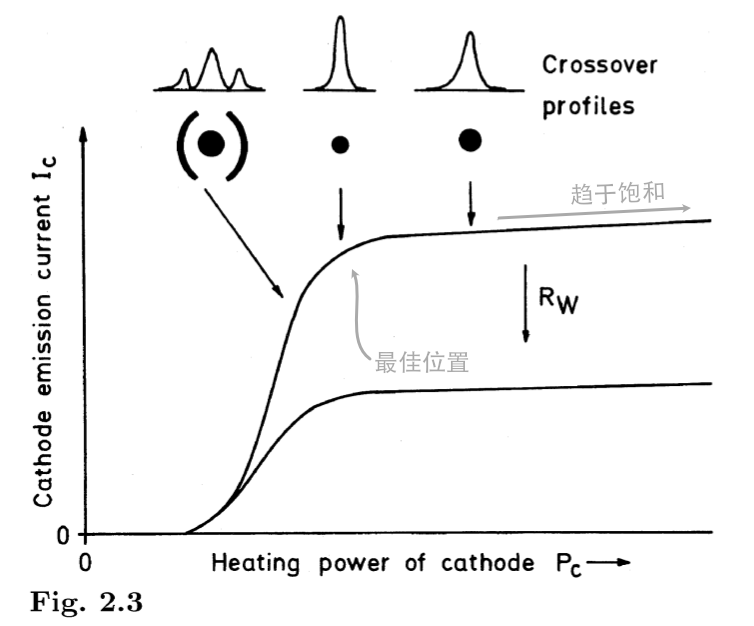
  (Fig.2.3. 一个自对中 (auto-biased) 热发射电子枪 发射电流 $I_c$ (cathode emission current) 和加热功率 $P_c$ 的关系, 以及其交叉斑的一个演示. )

• 交错斑 (crossover)

  为了获得最小的交叉斑, 应在 $I_c - P_c$ 接近转折点的位置.

  在交错斑处的电流密度近似满足高斯关系 (Gaussian profile):

  $$j(r) = j_0 \mathrm{exp}[- (\frac{r}{r_0})^2]$$

  其中 $r_0 ≅ 10 ∼ 50 μ m$.

  在最佳工作点位之后, 一个过热的电子枪, 会导致电子枪的使用时长缩短; 并且加热功率 $P_c$ 过大也会导致交错斑减少; 在最佳工作点位之前, 一个过冷的电子枪, 会导致交错斑发散 (非聚焦).

• 初始发射动量 ($\boldsymbol{p}$)

  电子枪的初始发射动量满足 Maxwell 的分布, 会导致发射的电子能量的一个 $Δ E$.

• 电子枪亮度 ($β$)

  单位立体角上的电流密度: $β = \frac{Δ I}{Δ S Δ Ω} = \frac{j}{π α^2} = \mathrm{const}$,

  $$β_{\mathrm{max}} = \frac{j_c}{π} [1 + \frac{E}{k T_c} (1 + \frac{E}{2 E_0})] ≅ \frac{j_c E}{π k T_c}$$

  对于钨灯丝来说, $E = 25keV, T_c = 2700K$, $β = (0.3 ∼ 2) × 10^4 A cm^{-2} sr^{-1}$, (这个数值对于 $\mathrm{LaB}_6$ 约要大 10 到 20 倍).

• 探针电流 (electron probe current) ($I_p$)

Schottky-Emission Guns

Field-Emission Guns

Measurement of Gun Parameters

电子枪的交错斑的影响因素:

• 阴极和栅极之间的高度 (一个可能的 参考)
• 工作电流 $I_c$ 和工作功率 $P_c$ (在工作曲线上的那个折点的选择)

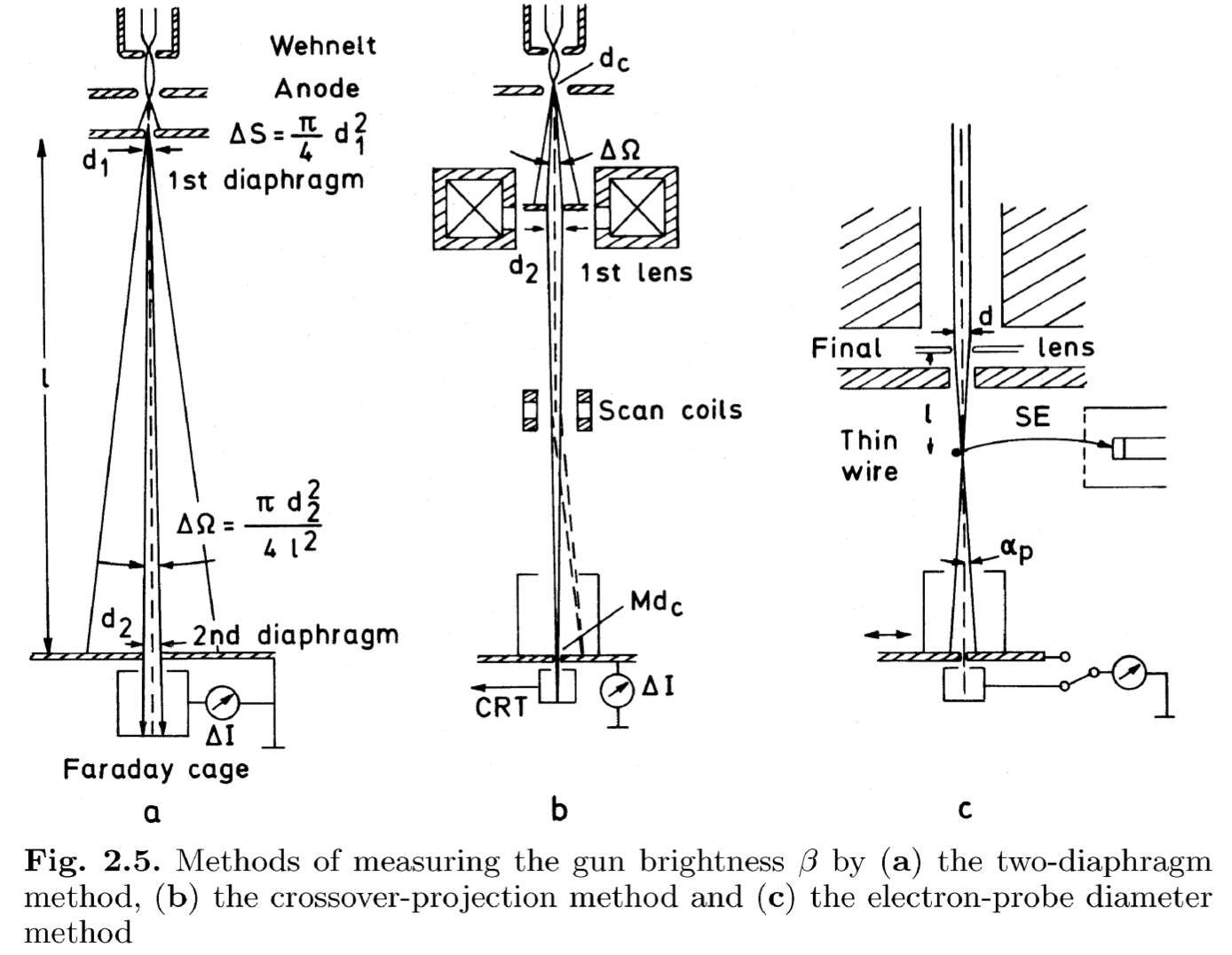
测量判断光强 $β = \frac{j}{Δ Ω}$ 的方法大致有如上三种: (原理上都需要测量 $Δ I, Δ S, Δ Ω$)

• Two-diaphragm Method
  • 一级光阑直径 $d_1 → Δ S = \frac{π d_1^2}{4}$, 需要满足其直径小于交错斑
  • 二级光阑直径 $d_2 → Δ Ω = \frac{π d_2^2}{4 l^2}$, 距离一级光阑的距离 $l = 10 ∼ 50 cm$.
  • 电流 $Δ I$ 通过法拉第笼来测量
• Crossover-projection Method

前两种方法不能用于 Schottky 和场发射的枪, 因为其源的尺寸较小.

• Electron-probe Diameter

Electron Optics

Focal Length of an Electron Lens

磁透镜的一个示意图:

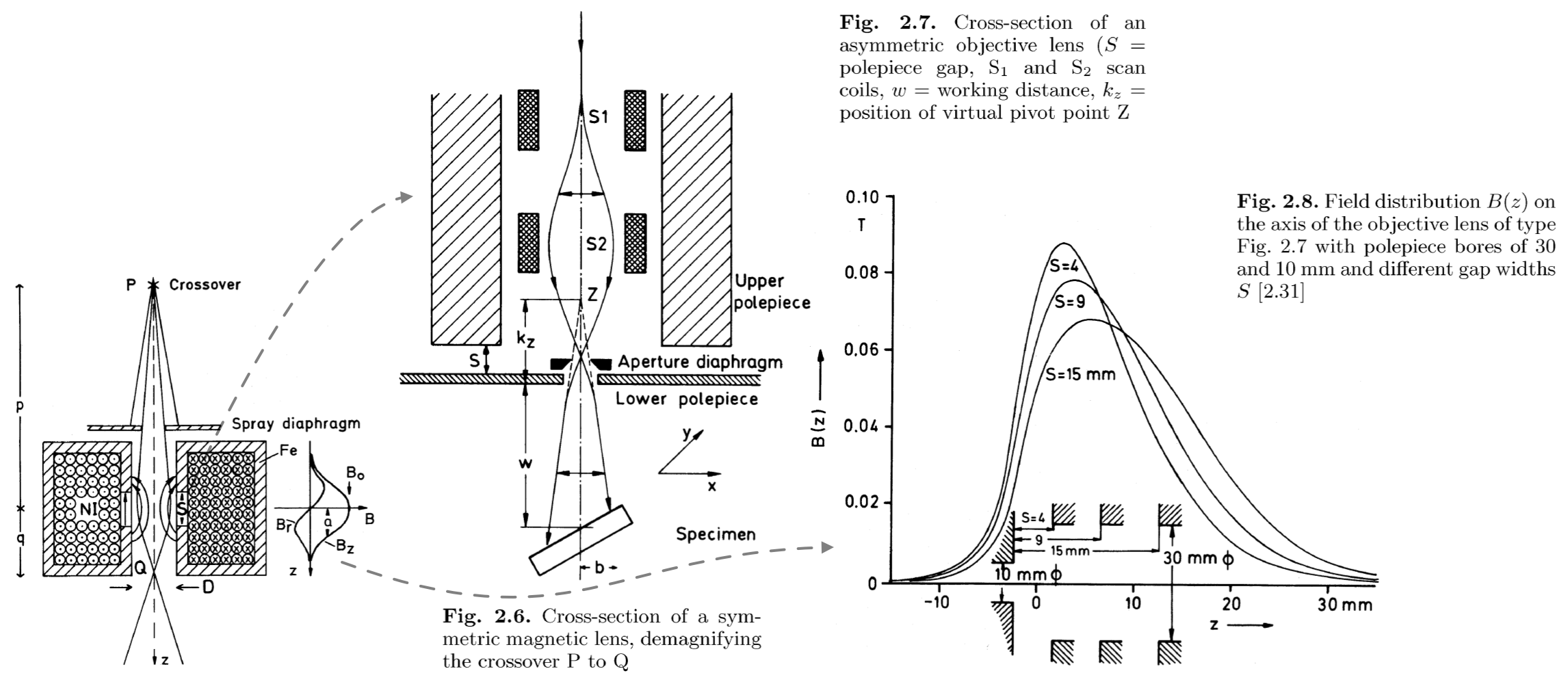
图片的一些说明

• 一个比较简单的线圈形式如 Fig 2.6 所示, 其中 $p$ 和 $q$ 分别为物距和像距.
• 在一个稍微更加详细一点的示意图中 $S_1$ 和 $S_2$ 为扫描线圈.
• 可以将最终的出射电子束近似为从 $Z$ 处发射的点粒子.

轴对称场中, 利用 $∇ ⋅ \boldsymbol{B} = 0$, 可以有 $B_r = - \frac{r}{2} ∂_z B_z$, 应当有受 Lorentz 力 $\boldsymbol{F} = - e (\boldsymbol{E} + \boldsymbol{v} × \boldsymbol{B})$. 目标是计算交错斑 P 经过透镜系统有得到的新的交错斑 Q 的位置. 因为在 SEM 中的透镜往往都是弱透镜 (? normally weak, 我个人认为应该是近轴条件), 所以可以用类似光学的焦距公式: $\frac{1}{f} = \frac{1}{p} + \frac{1}{q}$ 和放大率 $M = \frac{q}{p}$ 来进行表示.

并且有近似公式:

$$\frac{1}{f} = \frac{e}{8 m U} ∫_{- ∞}^{+ ∞} B_z^2 \mathrm{d}z$$

而磁透镜会引入一个旋转量:

$$\varphi = \sqrt{\frac{e}{8 m_0 U}} ∫_{- ∞}^{+ ∞} B_z \mathrm{d}z$$

对于 Fig. 2.6 中的钟形磁场分布, 有近似公式:

$$f = \frac{2a}{π k^2}, \varphi = π k \ \mathrm{for}\ k^2 = \frac{e B_0^2 a^2}{8 m U} \ll 1$$

其中, $a$ 为最大磁场强度 $B_0$ 的半宽长度. $k$ 表示了一个无量纲的透镜参数, 其衡量了磁透镜的强度.

• 物镜设计
  • 探射电子束经过的最后一个磁线圈被称为 物镜
  • 一般物镜的 ploepiece 会设计得较小一些, 防止磁场影响样品区域.

    其他的透镜可能会设计得较长一些, 以能够往里面塞偏转线圈 $S_1$ 和 $S_2$. (见 Fig 2.7)

    (关于间隙宽度 $S$ 对磁场的影响, 见 Fig 2.8. )

  • 常见的工作距离 $w$ 在 $5 ∼ 20 mm$ 之间.
  • 一般为了能够在物镜下挂载各种探测器, 会将其形状 (polepiece face) 设计为锥形, 且其平整部分的开孔直径约 $10 ∼ 20 mm$.
  • 物镜光阑应当能够让最后一束出射光顺利射出而不会受到衍射的影响.

Lens Aberrations

误差分析和修正:

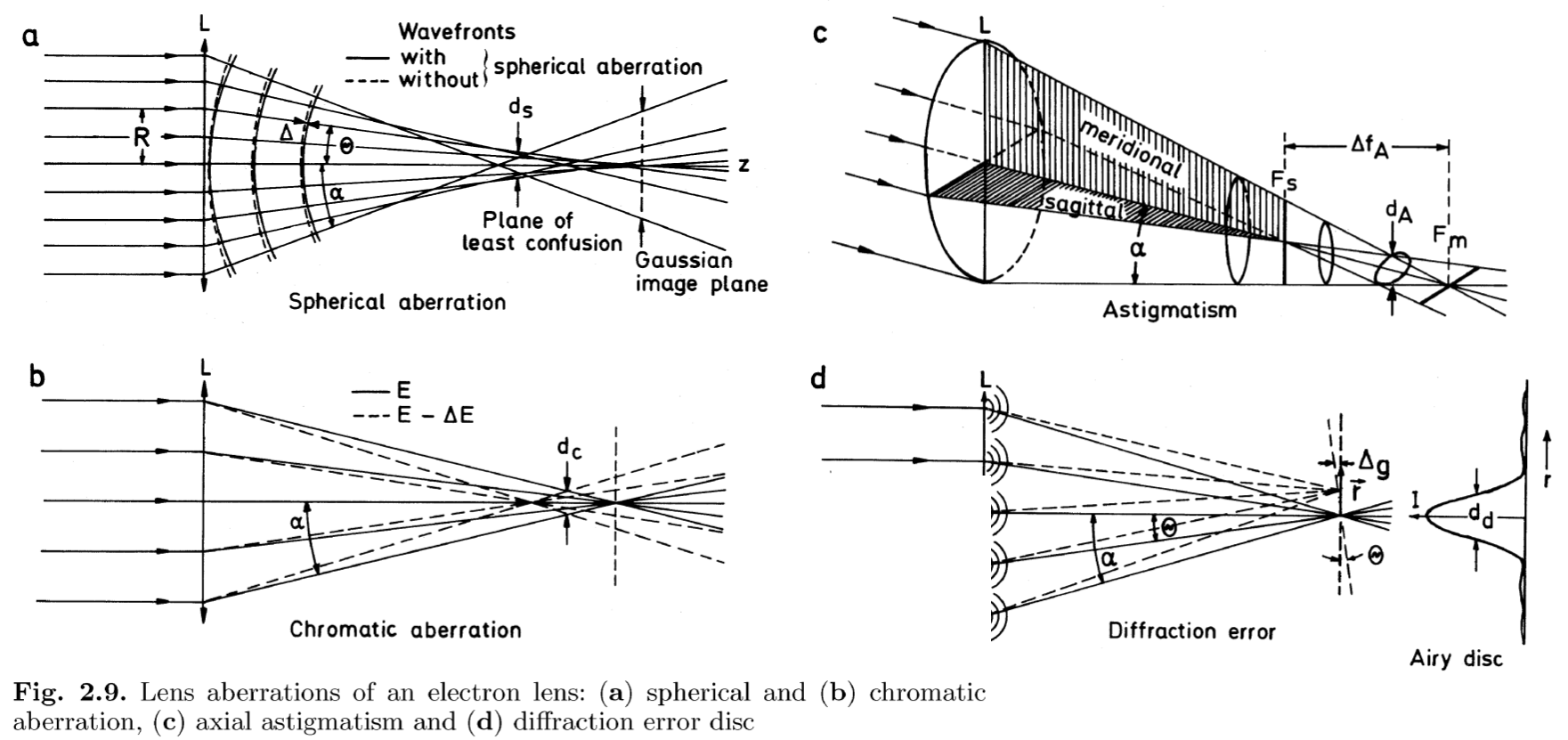
• Spherical Aberration (球差)

  (如果能有个动画来演示波前的移动就好了, 简单的解释就是, 对于从一点发出的波前会形成球面, 而透镜为平面, 从球面到平面上会有一个相位差, 反之同理, 从透镜平面没法汇聚到一个焦点上, 所以会有球差.)

  对 Gaussian 成像平面, 即近轴光线 (paraxial rays) 的焦平面, 其宽度为: $2 C_s α^3$, 而在光束最小处的直径为:

  $$d_s = 0.5 C_s α^3$$

  其中 $α$ 为由光阑约束的半角宽度, 可以通过改变物镜的光阑大小来改变; (对于 SEM 中使用的弱透镜 (? Weak lenses), 在较远的工作距离中会引入较大的球差), 球差参数大约是 $C_s = 20 ∼ 100 mm$, 并且其随着 $f^3$ 进行变化, 有近似公式 ($a$ 为上文中的磁场半宽):

  $$C_s ≅ \frac{3 f^3}{4 a^2}$$

  球差系数 $C_s$ 可以通过测量在物镜光阑移动到偏轴情况时的像的位移来得到.

• Chromatic Aberration (色散)

  因为焦距和能量有关, 所以在 $Δ E$ 的能量差下, 由于焦距差异导致的最小光束宽度为 (对于 $k^2 \ll 1$):

  $$d_c = C_c \frac{Δ E}{E} α$$

  其中 $C_c$ 为色散系数.

  色散往往是由于加速电压的波动引入的:

  $$\frac{Δ f}{f} = \frac{Δ U}{U} + 2 \frac{Δ I}{I}$$

  所以为了减少色散, 应使得 $\frac{Δ U}{U}$ 和 $2 \frac{Δ I}{I}$ 项都小于 $\frac{Δ E}{E} ≅ 10^{-4}$ 的一个波动. (因为 $\frac{Δ E}{E}$ 在低能量时受到能量变化影响更明显, 所以对于低能 LVSEM 情况下, 可能会需要通过一系列的电磁四极子来进行修正.)

  色散常数 $C_c$ 可以通过在光阑不在轴中心时测量加速电压变化时, 图像的一个偏移量来得到.

• Axial Astigmatism (轴向像散)

  磁场在磁导管 (ploepiece) 中不均匀的分布, 如椭圆型 (非圆) 的磁导管, 于是就会导致不同方向上焦距的不同:

  $$Δ f_A = \left| F_s - F_m \right|, d_A = Δ f_A α$$

  其中 $d_A$ 为光束极细处的直径.

  轴向像散可以通过一对在磁导管间隙的四极子透镜 (quadrupole lenses) 来修正.

• Diffraction Error (衍射误差)

  物镜光阑会产生圆孔衍射斑, 于是衍射斑有半宽:

  $$d_d = 0.6 λ / α$$

  其中 $λ$ 为电子波长.

• Correction of Lens Aberrations
  • 如 coma (彗差), distortion (畸变), 和离轴误差 (non-axial errors), 可以通过一个傍轴的电子束和一个小的光阑使得 $α \leq 20 m rad$
  • 可以通过增加 $E$ 来减少 $\frac{Δ E}{E}$ 来减少色差.
  • 引入四极子可以来消球差和色差

Special Designs of Objective Lenses

• In-Lens Operation
• Single-Polepiece Lenses
• Combinations with Electrostatic Fields
• Miniaturized SEM

Geometric Optical Theory of Electron-Probe Formation

• 缩小率

  通过计算交错斑在多个透镜叠加 (demagnification 缩小) 后的直径 $d_0$, 即得到最终照射在样品上的探测电流的直径 (认为每一个透镜中间产生的交叉斑图像 (crossover image), 就紧接着被下一个透镜放大, 但是认为是有一个较远的物距 $L$, 也就是认为这样的距离 $(\frac{1}{f} - \frac{1}{L})^{-1} ≅ f$, 于是对于一个三透镜系统):

  $$d_0 = \frac{f_1 f_2 f_3}{L_1 L_2 L_3} d_c = m d_c$$

  其中 $m \ll 1$ 为 缩小率.

• 透镜尺寸估计

  对于热发射电子枪 $d_c ≅ 20 ∼ 50 μ m$, 若需要使得探针直径 $d_0 \leq 10 nm$, 即缩小倍率 $m \leq 1 / 5000$, 于是需要 $\frac{f_i}{L_i} ≅ (\frac{1}{5000})^{1/3} ≅ \frac{1}{17}$. 若 $f_i = 5mm$, 那么最小两个透镜之间距离也需要 $3 L_i ≅ 25 cm$.

  对于 Schottky 或者场致发射的电子枪, 因为可以有更小的交错斑 ($< 10nm$), 所以即使只有一个物镜, 也能够达到更加 $d_0 ≅ 1nm$ 的效果.

• 透镜光阑半径估计

  物镜光阑半径 $r$ 影响探针尺度 $α_p$, 在一阶近似下有公式:

  $$α_p = r / f$$

  对于实际情况, 若光阑外有磁场泄漏, $α_p$ 可能会有一些不同. 对于光阑参数 $10 ∼ 20 mrad$ 量级, $f ≅ 5 ∼ 20 mm$ 的结果, 其光阑直径约为 $50 ∼ 200 μ m$.

  一般为了得到一个好的信噪比, 需要有至少 $I_p \geq 10^{-12} ∼ 10^{-11}A$, 一般对应的光阑量级约为 $d_{\mathrm{min}} ≅ 10 nm$, 以及 $α_{\mathrm{opt}} ≅ 5 ∼ 10 mrad$.

  当工作距离 $w$ 在 $10mm$ 的情况下, 对应的物镜光阑直径约为 $2 r ≅ 2 α_P w = 50 ∼ 100 μ m$.

• 探针电流估计

  

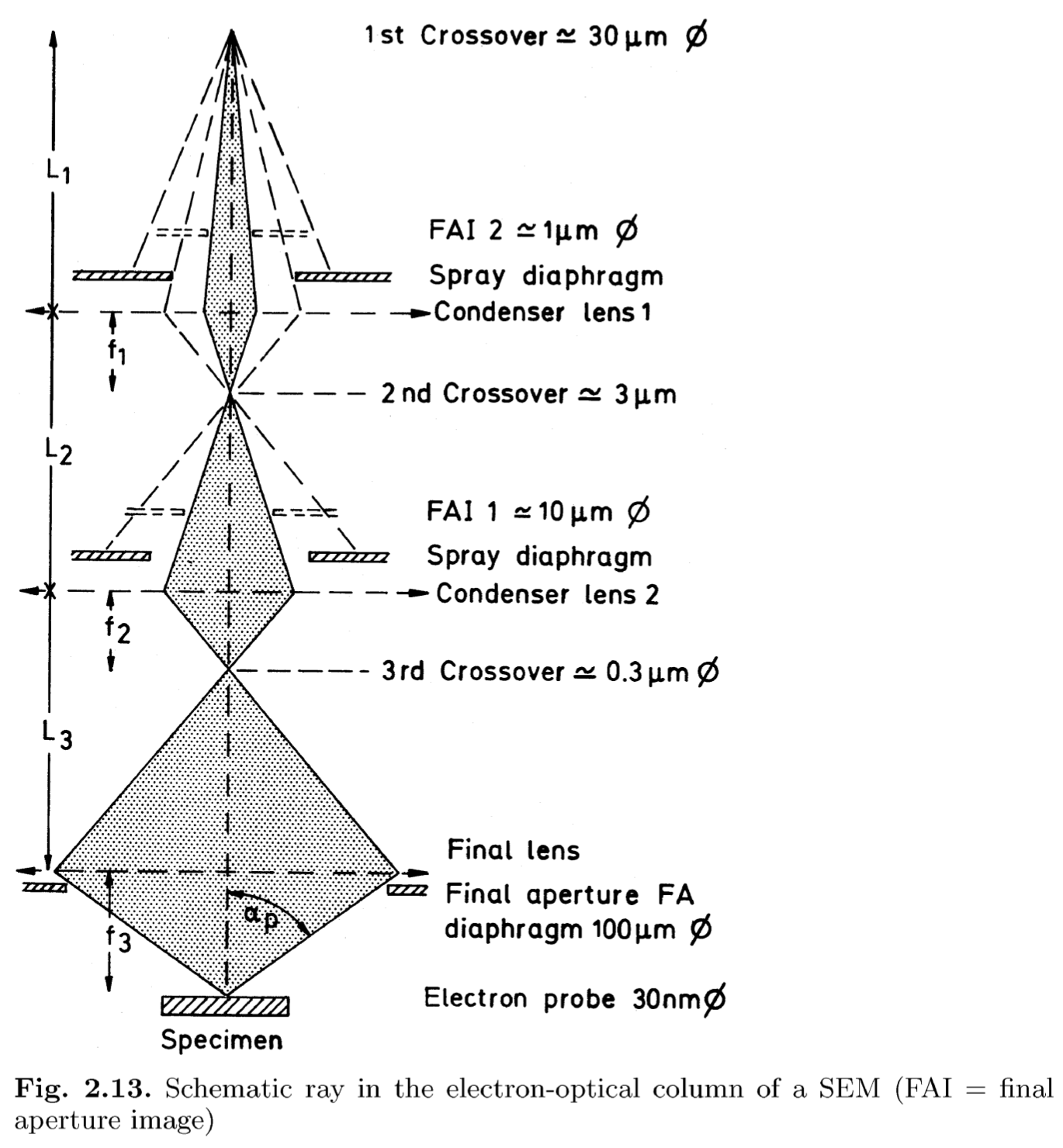
  $$j_P = π β α_P^2 ⇒ I_p = \frac{π}{4} d_0^2 j_P$$

  其中, $β$ 为枪的亮度参数 $β = \frac{j}{Δ Ω}$, $j = \frac{Δ I}{Δ S}$.

• 探针直径和成像误差

  对于成像得到的探针直径:

  $$d_0 = \sqrt{\frac{4 I_p}{π^2 β}} α_P^{-1} = C_0 α_P^{-1}$$

  在对光斑大小的影响参数 $d_s, d_c, d_d$:

  $$d_P^2 = d_0^2 + d_d^2 + d_s^2 + d_c^2 = [C_0^2 + (0.6 λ)^2] α_P^{-2} + \frac{1}{4} C_s^2 α_s^2 + (C_c \frac{Δ E}{E})^2 α_P^2$$

  

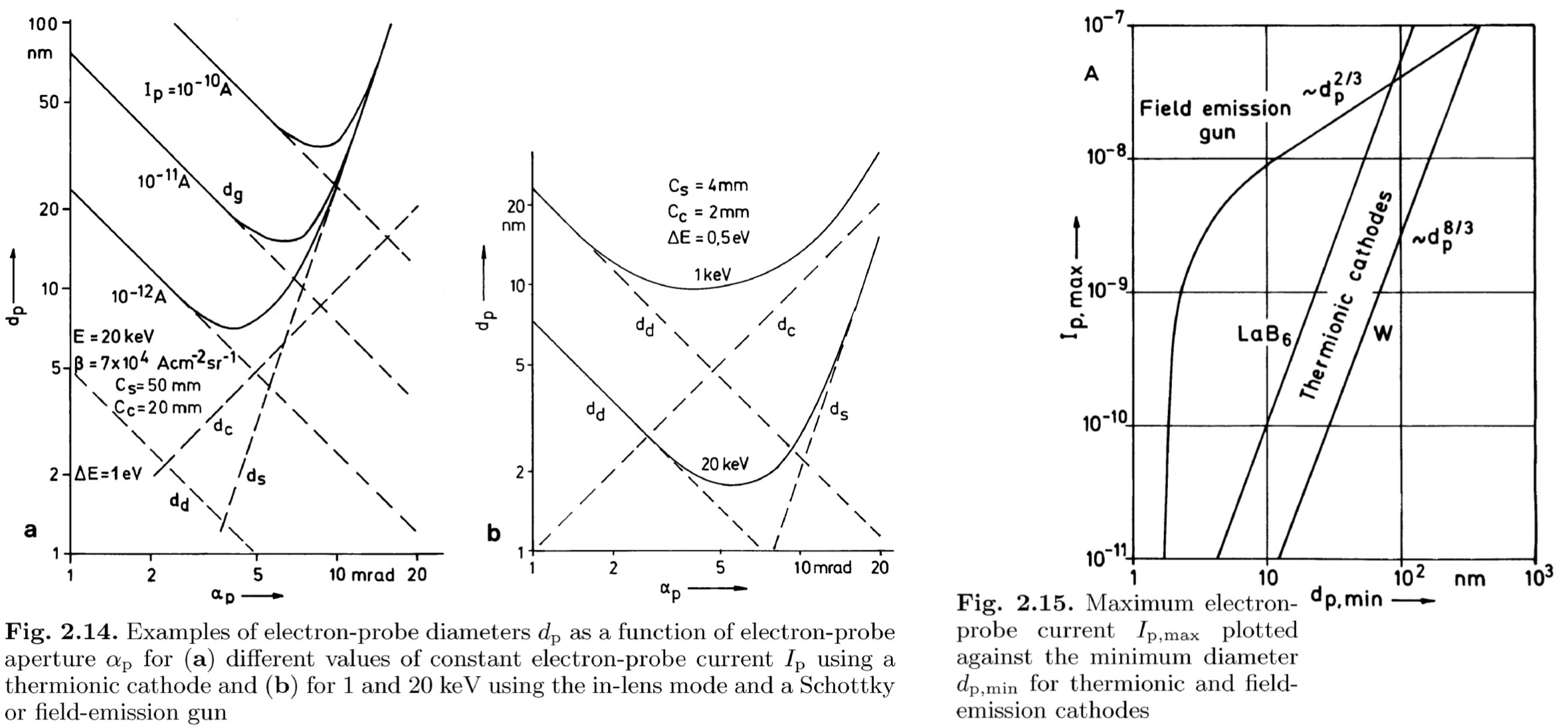
  • 一般在使用热发射的阴极的时候, 需要使得 $C_0 \gg λ$, 即使得衍射误差可以被忽略.
  • 除了 $C_0$ 项作为主导因素, $C_s$ (球差) 也是比较重要的一项, ($C_c$ 随着高的加速电压而减少).
  • 较小的光阑直径可以用来增加景深 (depth of focus), 较大的可以增强流强 (probe current), 但是不论是哪一种, 探针电流的直径都会增强并且会使得分辨率下降.
  • 在张角 $α_p < α_{\mathrm{opt}}$ 时, 有 $d_p \propto α_p^3$, 所以球差在在实际中会起一个比较并不是很大的作用, (because the real beam profile is then not Gaussian but consists of a peak and a broad background.)
  • 最佳张角 $α_{\mathrm{opt}}$ 可以通过 $\frac{∂ d_p}{∂ α_p} = 0$ 时计算得到的 $α_p = α_{\mathrm{opt}}$:

    $$α_{\mathrm{opt}} = (\frac{4}{3})^{\frac{1}{8}} (\frac{C_0}{C_s})^{\frac{1}{4}}$$

  • 在最佳张角时, 应有探针直径的最小值 $d_{p, \mathrm{min}}$:

    $$d_{p, \mathrm{min}} = (\frac{4}{3})^{\frac{3}{8}} (C_0^3 C_s)^{\frac{1}{4}}$$

  • 从中可以解得 $I_p$, 即最佳探测电流:

    $$I_{p, \mathrm{max}} = \frac{3 π^2}{16} β C_s^{- \frac{2}{3}} d_{p, \mathrm{min}}^{\frac{8}{3}}$$

    注: 在 Schottky 或场致发射电子枪来说, 其波长 $λ$ 在比 $C_0$ 更大, 因为其亮度 $β$ 更高, 所以可以得到一个更小的 $d_p$. 对于场致发射电子枪, 其电流强度有公式 $I_{p, \mathrm{max}} = c d_{p, \mathrm{min}}^{\frac{2}{3}}$, 其中 $c$ 为一个和电子枪电极和磁线圈球差有关的一个常数.

    [只能说某种程度来说, 真的是一开始了解的不多, 现在就十分的后悔. 不过对于热发射电子枪, 其好处是能够在较大的探针下, 有较高的电流. ]

  • 总结来说, 了解 焦距 $f$, 工作距离 $w$,
    • 对于一组最终的张角设置, $α_p$ 随 $f^{-1}$ 减少;
    • 对于相差和球差, 分别相对 $f^3$ 和 $f$ 增加, 其系数 $C_s$ 和 $C_c$ 和 $f$ 与 $w$ 差不多无关.

Wave-Optical Theory of Electron-Probe Formation

对于热发射电子枪, 波动光学项的部分可以暂时忽略; 对于 Schottky 和场致发射电子枪倒需要更进一步的考虑.

[但是我们用的又不是这俩, 到时候再说吧… 我波动光学不能说一窍不通, 学得乱七八糟肯定是的了.]

Electron Beam Deflection Modes

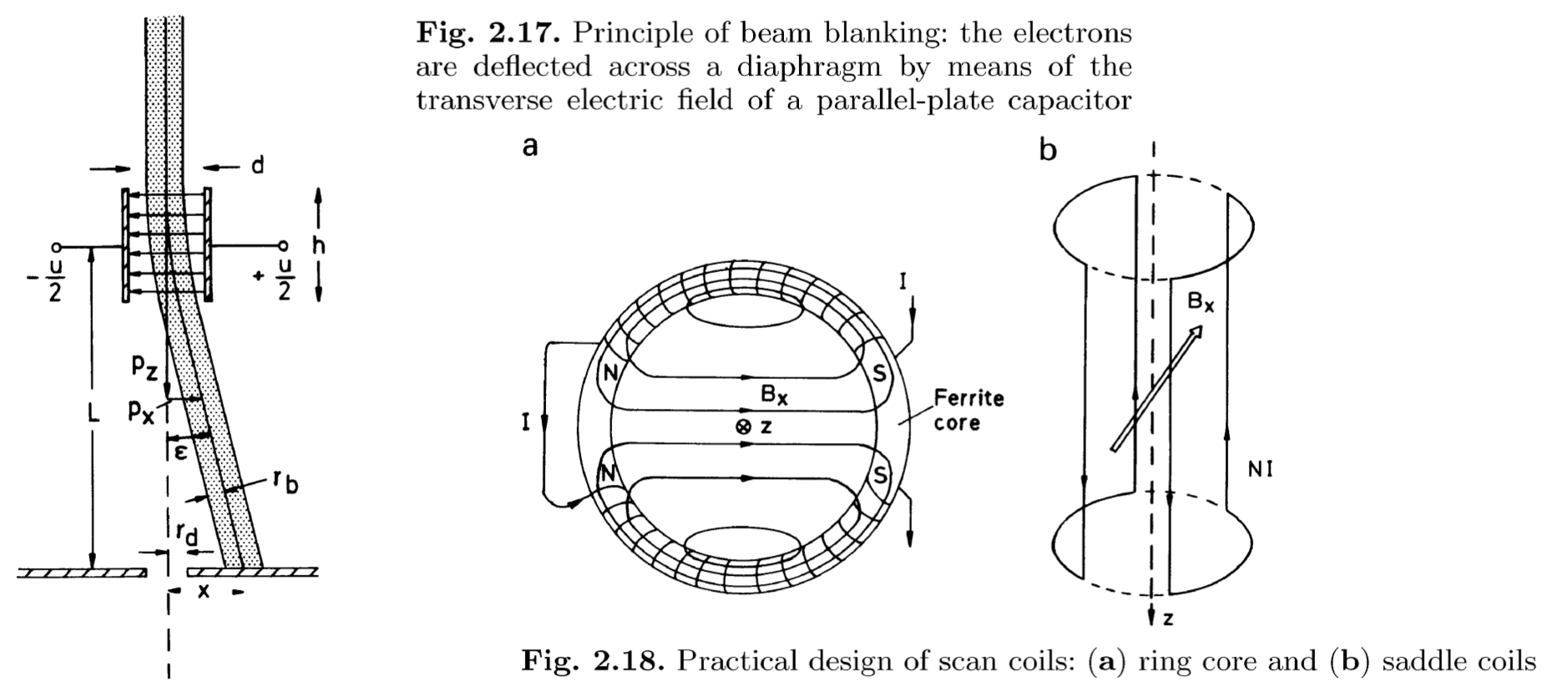
关于图片的一些说明

• 一般因为电偏转所需要的高压过高, 不方便使用, 所以往往采用磁透镜的设计

  对于 $20keV$ 量极的电子, 在偏转角约为 $ε = 5^{ˆ} ≅ 0.1 rad$ 时, 若电场距离 $h = 1 cm$, 偏转电场约为 $| \boldsymbol{E} | = u / d = 20kV$, 此时约需 $u = ± 2kV$ 的偏转电压; 类似的, 对于 $B = 10^{-2} T$ 的磁场, 在相同的偏转要求下, 约需要 $N I = 20 A ⋅ \mathrm{cols}$ 的量级.

  (因为要的电流比较小 $N=200, I = 0.1A$, 所以在磁偏转线圈的设计上比较轻松.)

• 磁透镜的两种设计中:
  • a. 图中的设计, 需要在其中加入铁芯
  • b. 图中的设计, 是一种不需要铁芯的设计, 其线圈形状为马鞍面

Electron Beam Deflection by Transverse Fields

在经过电场偏转 (Fig. 2.17) 或者是磁场偏转 (Fig. 2.18), 假设认为飞行时间 $Δ T = \frac{h}{v}$ 很短, 并且不考虑垂直偏转方向上的运动的影响. 即在偏转方向上获得的动量约为 $p_x = e (E_x + v B_y) Δ T$. 于是偏转角 $ε$ 约为:

$$ε = \frac{e h}{m v^2} E_x = \frac{h}{2d} \frac{u}{U} \frac{1 + E/E_0}{1 + E/2E_0}$$

(其中 $u$ 为偏转的电压)

或者是

$$ε = \frac{e h}{m v} B_y = \frac{e h B_y}{[2 m_0 E(1 + E/2E_0)]^{1/2}}$$

Scanning, Magnification and Rocking

两对偏转透镜 $S_1$ 和 $S_2$ 用于在 $x$ 和 $y$ 方向上产生偏转, 令偏转扫描的区域线度为 $b$, 在显示器上的线度 $W_B$, 于是整体的放大倍率:

$$M = \frac{W_B:\ \mathrm{Width}\ B\ \mathrm{of}\ \mathrm{the}\ \mathrm{CRT}}{b:\ \mathrm{Width}\ b\ \mathrm{of}\ \mathrm{the}\ \mathrm{scanned}\ \mathrm{area}}$$

• 为了减少衍射对成像的影响, 偏转后的光束应当仍然落在物镜光阑内.

Electron Beam Blanking and Chopping

Focusing

Focusing and Correction of Astigmatism

Depth of Focus

Dynamic and Automatic Focusing

整体光路设计

来一个简单的计算包:

;;; SEM-Calculate Package
(defpackage :sem-calculate
  (:use :cl))

;;; The following code are in SEM-Calculate Package
(in-package :sem-calculate)

没啥花里胡哨的目标, 就是为了能够辅助我来做一些简单的计算.

[Note: 程序没有写完, bug 仍需增长. 代码在 此 下载, 能不能跑不太好说… ]

一些基本的计算操作

这些基本的计算操作是为了能够拓展我写代码的方法, 如果你并不感兴趣, 那么可以跳过这一节, 我先把它给折叠了.

[Note: 并且这个基本还都在早期开发, 所以也是折叠的一个原因. ]

点我展开

突然发现这个部分写得并不是非常通用, 完全就是一个为了该项目的一个特化程序. 和我之前想要到的代数系统还是有点距离的…

单位

(暂时没有时间写)

积分和微分

离散积分

目前实现的离散积分通过两个点的矩形条积分, 梯形积分.

(defun discreate-integrate (points &key (method 'trapezoid))
  "Discreat integrate the POINTS, which would be like a list of points.

Methods are `rectangle', `trapezoid' 
or other possible function for `point1', `point2'.
Points are like `(x . y)'.

+ rectangle                + trapezoid

  |             +            |          ...+
  |     +-------|            |     +#######|
  |     |#######|            |    /|#######|
  |     |#######|            |   /#|#######|
  | +---|#######|            |  +##|#######|
  +---------------           +---------------

or if you provide a custom function, it should calculate the
area defined by two points."
  (labels ((rectangle (point1 point2)
             (let ((x1 (car point1)) (y1 (cdr point1))
                   (x2 (car point2)))
               (* y1 (- x2 x1))))
           (trapezoid (point1 point2)
             (let ((x1 (car point1)) (y1 (cdr point1))
                   (x2 (car point2)) (y2 (cdr point2)))
               (/ (* (+ y2 y1) (- x2 x1)) 2)))
           (iter (points method)
             (if (> (length points) 1)
                 (+ (funcall method (first points) (second points))
                    (iter (rest points) method))
                 0)))
    (iter points (cond ((eq method 'rectangle) #'rectangle)
                       ((eq method 'trapezoid) #'trapezoid)
                       (t method)))))

为了减少误差, 可以增加每次的采样点, 使得采样点能够数量更多 ($> 2$), 于是就能够增加精度. (注: Boole's Rule 的表可以在 Wolfram MathWorld 上找到)

(defun discreate-integrate-dx (fs dx &key (sample 2))
  "Discreate integrate of POINTS using SAMPLE number."
  (let ((series
          (cond ((eq sample 1) '(1))
                ((eq sample 2) '(1/2    1/2))
                ((eq sample 3) '(1/3    4/3     1/3))
                ((eq sample 4) '(3/8    9/8     9/8     3/8))
                ((eq sample 5) '(14/45  64/45   8/15    64/45   14/45))
                ((eq sample 6) '(95/288 375/288 250/288 250/288 375/288 95/288))
                (t              (throw 'user "Unsupported sample.")))))
    (labels ((iter (points)
               (if (>= (length points) sample)
                   (+ (reduce
                       #'+
                       (mapcar (lambda (k f) (* k f dx)) series
                                      (subseq points 0 sample)))
                      (iter (nthcdr (1- sample) points)))
                   0)))
      (iter fs))))

唯一的一个缺点就是在当前问题中可能并不能用… 并且那个表格也不是很美观.

(并且这个应该并不是我需要专注的一个问题, 所以)

离散微分

(defun discreate-differential (point1 point2)
  "Discreate differential of two points POINT1 and POINT2."
  (let ((y1 (cdr point1)) (x1 (car point1))
        (y2 (cdr point2)) (x2 (car point2)))
    (/ (- y2 y1) (- x2 x1))))

目标是能够根据所需放大率 (缩小率 $m$) 来设计光路 [几何光学程度]

不要笑我没有文化, 因为懒得搞波动光学, 这里就简单先用几何光学的程度凑合一下先.

最终缩小率 (demagnification rate) 为 $m$:

(defun demagnification-rate (&rest lens)
  "Given a set of LENS, return the demagnification rate of the crossover.

The calculation equation is described below when object distance is large enough:

           f1 * f2 * ... * fn
    d0 = ---------------------- * dc = m * dc
           L1 * L2 * ... * Ln

where the `m' is the demagnification rate, `dc' is the crossover of the gun,
`d0' is the final electron probe diameter (with 0 rank aberration). "
  (let ((focal-length   (mapcar #'len-focal-length    lens))
        (large-distance (mapcar #'len-work-distance lens)))
    (reduce #'* (mapcar (lambda (f L) (/ f L))
                        focal-length
                        large-distance))))

一些设计的思考:

• 目前是需要根据已有的透镜信息去组建一个透镜系统, 而这样的透镜系统却还有很多的信息是
  • 虽然不知道但是 可以 (比较快) 测量 的:
    • [ ] 电子枪的电流和功率关系 $→$ 最佳工作点 find-opt-heating-power-point
    • [ ] 正常工作电子枪 $→$ 测量电子枪亮度 $β$ measure-gun-brightness-two-diaphragm
    • [ ] 透镜设计 $→$ 轴上磁场 $→$ 焦距 $f$ calculate-focal-length-by
    • [ ] 目标缩小倍率 $m \overset{f_i}{→} L_i$ 透镜距离
    • [ ] 电子枪亮度 $β →$ 目标工作的探针电流 $I_p \overset{I_p = j_p Δ Ω}{→}$ 光阑参数 $α_p \overset{f}{→} r$ 光阑半径
  • 不知道也不太方便测量, 需要进一步调研的:
    • 电子枪的交叉斑 $d_c$ (虽然目前还不清楚如何测量, 但是肯定需要先得到转折点).

      原则上来说, 阴极和栅极之间的高度会影响交错斑, 那么对于目前电子枪设计确定的情况下, 应该是一个确定的, 待测量的量.

      假如在粗略的量级估计的话, 那么就目前假设为 $d_c = 50μ m$

一些部件的说明

(热发射) 电子枪的信息的处理

• 工作电流 $I_c$ 和工作功率 $P_c$ 的工作曲线

  需要测量电子枪工作时候的工作电流和两端电压,

  工作电流 $I_c$	工作电压 $U_c$	工作功率 $P_c$

  绘制工作曲线并找到转折点.

  这里认为当 $\frac{\mathrm{d} I_c}{\mathrm{d} P_c} \simeq 0$, 即足够小的情况下, 认为达到转折点.

  (defun find-opt-heating-power-point (data threshold)
    "Try to find turning point in DATA where differential is less than THRESHOLD.
  
  Return value are the first point found with T or last point when not found with NIL."
    (if (< (length data) 2)
        (values (car (first data)) NIL)
        (let* ((point1   (first data))
               (point2   (second data))
               (diff-abs (abs (discreate-differential point1 point2))))
          (if (<= diff-abs threshold)
              (values (car point1) T)
              (find-opt-heating-power-point (rest data) threshold)))))
  

• 电子枪的 亮度 ($β = \frac{j}{Δ Ω}$)

  当前的想法是通过双光阑法来进行测量.

  (defun measure-gun-brightness-two-diaphragm (diameter1 diameter2 length current)
    "Measure gun brightness with DIAMETER1, DIAMETER2, LENGTH and CURRENT.
  
  The gun brightness is measured by:
  
         jc        ΔI           π * d1^2         π * d2^2
    β = ---- = ---------, ΔS = ----------, ΔΩ = ----------
         ΔΩ     ΔS * ΔΩ            4              4 * l^2
  
  where d1 is DIAMETER1, d2 is DIAMETER2, l is LENGTH, ΔI = CURRENT."
    (let ((ΔS (/ (* pi diameter1 diameter1) 4))
          (ΔΩ (/ (* pi diameter2 diameter2) (* 4 length length))))
      (/ current (* ΔS ΔΩ))))
  

• 电子枪的 交叉斑 ($d_c$)

磁透镜的信息的处理

Some Conversions

描述一个透镜应该需要知道的信息:

• 焦距 $f$
• 工作距离 $w$ (或者说 $L$, 更加通用一点的说的话)
• 光阑大小 $r$ (根据光阑大小可以计算得到张角 $α$)

;;; To measure a len:
;;;   + Focal Length
;;;   + Object Distance
;;;   + Working Distance
;;;   + diaphragm-radius
(defstruct len focal-length object-distance working-distance diaphragm-radius)

计算焦距

使用近似公式来计算焦距 $\frac{1}{f} = \frac{e}{8 m U} ∫_{-∞}^{+∞} B_z^2 \mathrm{d}z$, 通过模拟来计算磁场在轴上的分布.

下面的程序主要是计算焦距 $f$, 不过这部分感觉对实际使用没有啥大作用, 所以折叠起来了.

Detailed Dirty Works

假设有数据如下 (由下面的 COMSOL 模型计算得到, COMSOL 教程可见 Learning Note: COMSOL):

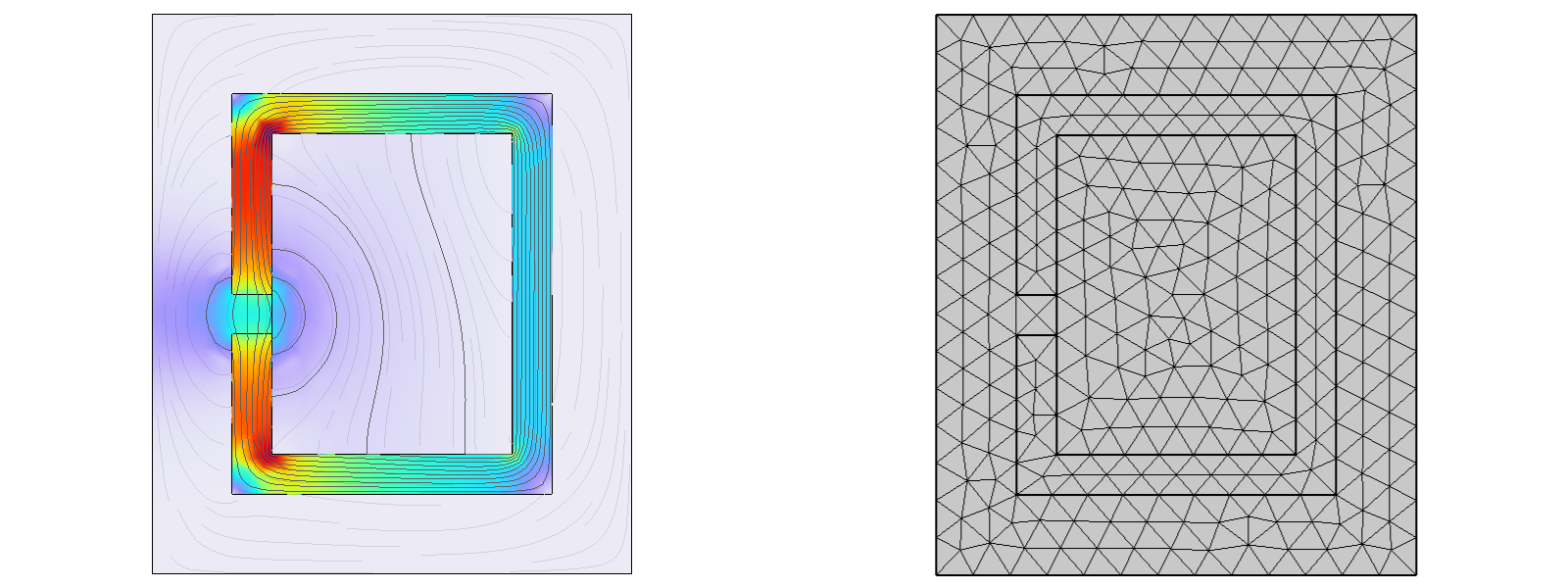
(注: 因为这个就只是一个测试用的例子, 所以画的网格很稀疏, 并且透镜设计也很随便. 计算文件可以从 这里 下载.)

r	z	mf.Bz (T)	mf.Mr (A/m)	mf.normB (T)
0	-10.666666666666671	1.4646716694325223E-5	0	1.4646736282555131E-5
0	-19.999999999999986	1.462952112072278E-20	0	1.2397894072218481E-8
0	-1.3333333333333286	5.108795667969144E-5	0	5.1105374623999824E-5
0	8.000000000000014	1.5346787163236976E-4	0	1.5347757156018547E-4
0	17.33333333333333	4.5491279693352224E-4	0	4.549141911877454E-4
0	26.66666666666667	0.0012704782970466223	0	0.0012705074721924786
0	36.00000000000002	0.0028701697952111995	0	0.0028705728135869552
0	45.33333333333334	0.003966394239261433	0	0.00396639838522708
0	54.66666666666671	0.002745345253223525	0	0.0027457294402619768
0	64.00000000000004	0.0011874316185280164	0	0.0011874694904029466
0	73.33333333333337	4.2375853085136156E-4	0	4.2375898740568704E-4
0	82.66666666666674	1.4354038174382633E-4	0	1.4354523224501743E-4
0	92.00000000000007	5.1276710248094924E-5	0	5.130430039449734E-5
0	101.33333333333341	1.7112673591126424E-5	0	1.711841627443607E-5
0	110.66666666666677	5.607168178570042E-6	0	5.6072674592129275E-6
0	120	-1.771530382645302E-23	0	5.899865471892914E-9

可以绘制轴上磁场:

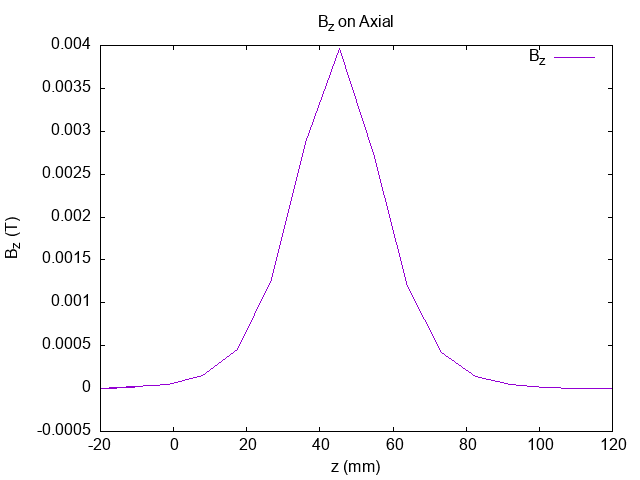
焦距的简单积分:

(let ((data (mapcar (lambda (row) (cons (nth 1 row) (* (nth 2 row) (nth 2 row))))
                    bz-on-axial)))
  (discreate-integrate data :method 'trapezoid))

0.00032637385

关于数据的读取

当前我并没有写一个很好的数据读取的一个操作, 因为我目前还不是很了解 Common Lisp 中的正则表达式和文件读取, 尽管应该不麻烦, 暂时还就是直接用 Org-Mode 中的表格来实现吧… 毕竟太麻烦了.

(有空再补充… )

于是可以计算得到最终的一个焦距表达式:

(defun calculate-focal-length-by (bz-points acc-U)
  "Provide BZ-POINTS on axial and accelerate voltage ACC-U (in SI Unit).

The focal length is calculated by:

    1         e         + ∞   
   --- = ----------- * ∫ Bz² dz
    f     8 * m * U   - ∞

to approximate, integration will only integrate at the provide BZ-POINTS,
which means BZ-POINTS shall be prefixed with a start and end or the start
and end point value is small enough to omit.

All the parameters provided should be in SI Unit. 
     e                                        C
The --- having the value: 1.758820024x10⁺¹¹ -----.
     m                                        kg

The functions returns f."
  (let* ((bz-square (mapcar (lambda (point) (cons (car point)
                                                  (* (cdr point) (cdr point))))
                            bz-points))
         (int-bz-square (discreate-integrate bz-square))
         (charge-to-mass-ratio 1.758820024E+11))
    (/ 1 (* int-bz-square (/ charge-to-mass-ratio
                             (* 8 acc-U))))))

(let ((bz-points (mapcar (lambda (row) (cons (nth 1 row) (nth 2 row))) bz-on-axial))
      (acc-U     5000))
  (calculate-focal-length-by bz-points acc-U))

0.0006968524

(注: 大约是 $0.6mm$ 量级的一个透镜, 显然这个结果是不太好的… )

磁透镜的误差估计

如何达到最佳工作的工作条件

• 若只有一级透镜 (仅有物镜), 则 $L = \frac{f}{m}$

  (defun measure-len-by-demagnification-rate (m len)
    "Return a new len by LEN parameters maximizing demagnification rate M. 
  
  The working distance L (or w) is calculated by L = f / m, 
  where f is the focal length, m is the demagnification rate."
    (let* ((new (copy-structure len))
           (mR  (if (< 1 m) (/ 1 m) m))
           (f   (len-focal-length new))
           (L   (/ f mR)))
      (setf (len-object-distance new) L)
      new))
  

• 考虑中间透镜, 应满足误差最小
• 若有两级即以上透镜, (显然, 只有最后一级 (物镜) 的工作距离是可调的), 对于非最后一级透镜, 选择使得误差最小的透镜参数.

  (defun measure-lens-by-demagnification-rate (m &rest lens)
    "Return a list of new LENS to archive the demagnification rate M.
  
  Since the demagnification rate m is calculated by:
  
         f1 * f2 * ... * fn
    m = --------------------
         L1 * L2 * ... * Ln
  
  if there's only one (object) len, its object length shall be f / L, 
  or if there's more than one lens, they shall archieve the minimum aberraation."
    (let ((len (first lens)))
      (if (null (rest lens))
          (list (measure-len-by-demagnification-rate m len))
          (cons (measure-len-by-aberration len)
                (apply #'measure-lens-by-demagnification-rate (cons next-m (rest lens)))))))
  

想要知道最终的探针的直径 (probe current diameter)

(defun electron-probe-aperture (len)
  "The electron probe aperture ɑₚ is calculated by r/f."
  (let ((r (diaphram-radius-of len))
        (f (focal-length-of    len)))
    (/ r f)))