切伦科夫计数器和穿越辐射探测器

稳定粒子的质量不能直接测量, 通过两个运动学物理量来反应粒子质量:

  • 入射带电粒子速度 \(←\) 切伦科夫辐射
  • 带电粒子相对论性时间扩展因子 \(γ\) \(←\)穿越辐射

通过这两个现象可以结合动量和能量的测量来确定粒子质量 \(→\) 鉴别粒子种类:

\[m = \frac{p}{β γ c} ⇒ \frac{\mathrm{d} m}{m} = \sqrt{(γ^2 (\frac{\mathrm{d} β}{β})^2)^2 + (\frac{\mathrm{d} p}{p})^2}\]

切伦科夫计数器

基本特征和公式

切伦科夫辐射性质

/_img/particles/cherenkov-theta-with-particle-beta.svg

对于飞行方向和切伦科夫辐射方向夹角为 \(θ\) 的粒子, 发生切伦科夫辐射的条件:

\[θ_c = cos^{-1} \frac{1}{n β}\]

  • 气体介质近似: \(θ_c → 0, θ_c ≈ \sqrt{2 (1 - \frac{1}{n β})}\)
  • 阀速度 (发生切伦科夫辐射的最小速度): \(β_t = \frac{1}{n}\).
  • 单位长度辐射能量: \(\frac{\mathrm{d} E}{\mathrm{d} x} = \frac{4 π^2 z^2 e^2}{c^2} ∫_{n β > 1} (1 - \frac{1}{n^2 β^2}) ν {\mathrm{d} ν}\)
  • 单位长度单位光子能量间隙产生的光子数: \(\frac{\mathrm{d}^2 N}{\mathrm{d} E \mathrm{d} x} = \frac{α^2 z^2}{\hbar c} sin^2 θ_c\)

    于是可以计算得到切伦科夫辐射光谱: \(\frac{\mathrm{d}^2 N}{\mathrm{d} λ \mathrm{d} L} = \frac{2 π α z^2}{λ^2} sin^2 θ_c\).

  • 在长度为 \(L\) 的介质中, 放出波长 \(λ_1 ∼ λ_2\) 之间的光子总数为: \(N = ∫_0^L ∫_{λ_1}^{λ_2} (\frac{\mathrm{d}^2 N}{\mathrm{d} x \mathrm{d} λ}) \mathrm{d}x \mathrm{d}λ = ∫_{λ_1}^{λ_2} \frac{2π L α z^2}{λ^2} sin^2 θ_c \mathrm{d}λ\), 即对应了切伦科夫光子密度分布.

    在可见光波段 \(400 \mathrm{nm} ∼ 700 \mathrm{nm}\), 近似有 \(\frac{N}{L} = 490 sin^2 θ_c\).

  • 发光时间取决于穿越时间
  • 能损相较于电离能损是可以忽略的 (无损探测方法).

探测器特征

  • 灵敏度可以通过向紫外区拓展的方式达到 (见上光谱公式, 可知 \(\frac{\mathrm{d}^2 N}{\mathrm{d}λ \mathrm{d}L} \propto \frac{1}{λ^2}\), 故在短波长处数量更多. 那为什么是绿色可见光?)
  • 切伦科夫计数器组成
    • 切伦科夫辐射体

      切伦科夫计数器的介质要求:

      • 电离能损小 (损耗)
      • 无 (少) 荧光发射 (无光噪声)
      • 光学色散小 (连续谱, 减少因为色散导致的计数器峰宽度, 分辨率更高)

        色散对切伦科夫计数器的速度分辨率的影响如下:

        \[\frac{Δ β}{β} = tan(λ) Δ θ \overset{cos θ_c(λ) = \frac{1}{n(λ) β}}{⇒} Δ θ_{\mathrm{DISP}} = \frac{Δ n}{n tan θ_c(λ)}\]

      • 对切伦科夫辐射透明度好 (切伦科夫光子损耗少)
      • 和光探测器光谱频响匹配 (探测器增益峰, 最大灵敏附近)
    • 光传输和收集系统

      对光子数进行积分, 可以得到探测的光电子数. 假设折射率 \(n\) 和波长 \(λ\) 以及长度 \(L\) 依赖较弱, 则有:

      \[N_{pe} = L N_0 sin^2 θ_c\]

      \[N_0 = \frac{2 π α}{h c} ∫ Q_{\mathrm{eff}}(E) Π_i ε_i(E) \mathrm{d}E\]

      • \(Q_{\mathrm{eff}}\) 为光电转换材料的量子效率
      • \(ε_i\) 是光传输, 收集相关的效率: 辐射体中的透过率, 探测器窗透过率, 镜子反射率, 电子学阀值造成的接受效率等
        • 探测器窗透过率可以通过透紫外光的石英窗等来实现,

          说得高级一些, 应当使得窗的 透过率曲线 和切伦科夫辐射 波长范围 以及光探测器的 光谱响应 相匹配

        • 镜子反射率可以通过镀层来提高 (镀 \(\mathrm{Al}\) 并覆盖 (约 \(∼ \frac{λ}{2}\) 厚度) \(\mathrm{MgF_2}\))
        • 需要对光学系统的像差进行补偿, 需要能够尽量适用于紫外光区域的光学系统
      • 好的 \(N_0\) 约 \(100\) 量级
    • 光探测器

      需要对紫外光透过率好 (集中在短波), 高灵敏度低噪声 (光子数少), 主要有:

      • 真空器件: 透紫外高灵敏低噪声的光电倍增管 (PMT), 微通道板 (MCP) 型光电倍增管, 多阳极光电倍增管
      • 固体光探测器: CCD, 光电二级管 (PD), 雪崩光电二级管 (APD), 可见光计数器 (VLPC)
      • 光敏气体探测器: 光电转换和电荷倍增

几种不同的切伦科夫计数器设计

  • 阈式切伦科夫计数器: 探测速度超过辐射阈速度 (由折射率 \(n\) 决定) 的带电粒子探测器, 可以用来从动量相同的混合粒子束中选出一种粒子.
  • 微分式切伦科夫计数器: 通过测量切伦科夫角来鉴别粒子
  • 环形成像切伦科夫计数器 (RICH)
  • 探测全反射切伦科夫光的计数器 (DIRC)
  • 切伦科夫 (相关) 定时计数器 (CCT)
  • 切伦科夫传播时间计数器 (TOP)

穿越辐射计数器

穿越辐射特性

  • 产生和介质瞬时极化相关

量能器

通过和带测粒子相互作用将粒子能量转换为可以测量的信号 (闪烁光, 切伦科夫光, 电离电荷等), 间接测量被测粒子的能量. 一般需要一下的特性:

  • 既能探测带电粒子又能探测中性粒子
  • 对于电子, \(μ\) 子, 强子具有不同的响应特征, 因而可以提供鉴别粒子的信息
  • 由于量能器可以分割为小单元, 它可以精确地给出入射粒子的位置和方向
  • 由于量能器原理建立在统计过程的基础上, 能量测量精度随能量升高而改善, 这与其他探测器不同.
  • 量能器的几何尺寸随入射粒子能量的增加呈对数增长, 而磁谱仪的几何尺寸 (在保持相同动量分辨率的条件下) 随动量的方根 (\(\sqrt{P}\)) 增长. 所以在高能条件下, 量能器可以有较小的尺寸.
  • 量能器的时间响应可以很快 (\(\leq 100 \mathrm{ns}\)), 也可以在高计数率环境下工作. 另外, 还可以利用能量沉积的模式组成事例选择的触发信号, 对感兴趣的事例进行选择.

电磁量能器

电磁簇射 (韧致辐射和电子对产生过程). 过程示意如下:

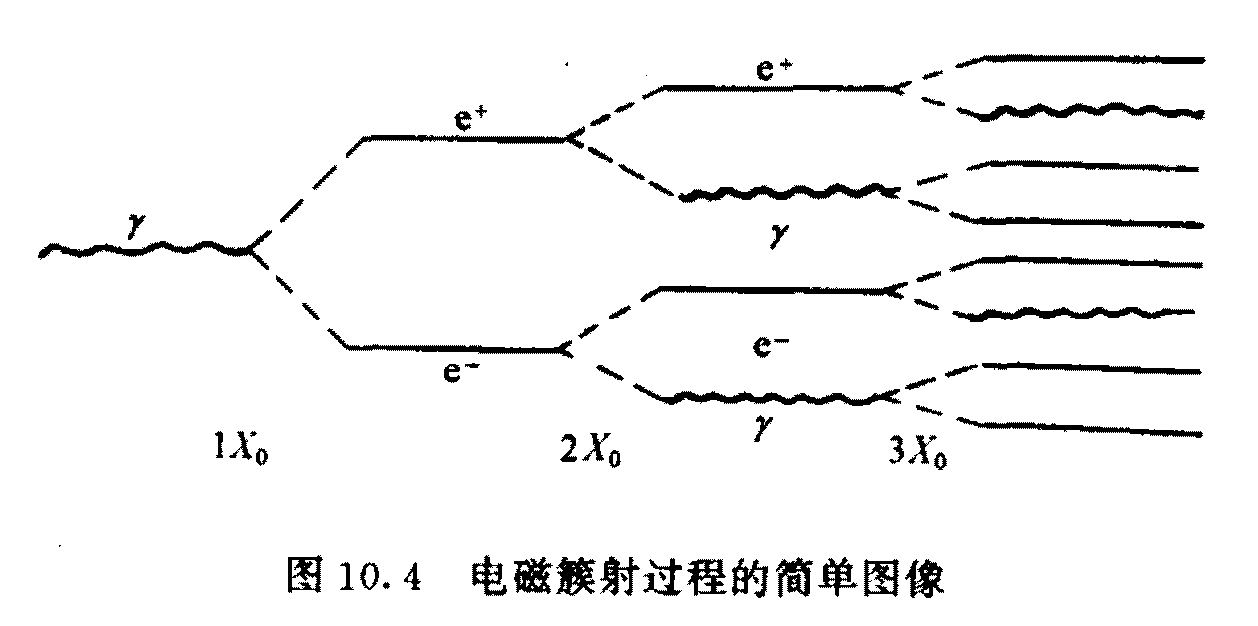
/_img/particles/air-shower.png

簇射产生的次级粒子总数:

\[n_{\mathrm{total}} = ∑_0^{n_{\mathrm{max}}} 2^n = 2(2^{n_{\mathrm{max}}} - 1) ≈ 2.2^{n_{\mathrm{max}}} = 2 \frac{E}{E_c}\]

积分路径长度 \(S\) 近似表达式 (\(S_0\) 为临界能量电子路程长度):

\[S = \frac{2}{3} X_0 ∑_{v = 1}^n 2^v + S_0 (\frac{2}{3}) N_p = [(\frac{4}{3}) X_0 + (\frac{2}{3}) S_0](E / E_c)\]

随机过程通过使用 Monte-Carlo 方法进行模拟计算 (EGSnrc).

  • 电磁簇射物理量
    • 辐射长度 \(X_0\): 高能电子从由于韧致辐射损失能量到达原来的 \(\frac{1}{\mathrm{e}}\) 的距离

      \[X_0 = \frac{716.4 (\mathrm{g ⋅ cm^{-2}}) \mathrm{A}}{Z (Z + 1) ln (\frac{287}{\sqrt{Z}})} ≈ 180 \frac{A}{Z^2} (\mathrm{g ⋅ cm^{-2}})\]

      在混合物 (化合物) 中, 近似为:

      \[\frac{1}{X_0} = ∑ \frac{f_i}{X_i}\]

      \(f_i\) 为重量比.

    • 临界能量 \(E_c\): 电离能损和辐射能损相等时的带电粒子的能量. 对于电子的近似表达式:

      \[E_e = \frac{800 \mathrm{MeV}}{Z + 1.2}\]

      代表带电粒子能量主要通过电离能损耗散到簇射增长的分界线.

    • 横向发展 Moliere 半径 \(R_m\): 在临界能量电子穿过 \(X_0\) 物质层时, 由于多次库仑散射造成的平均偏移的度量:

      \[R_m = X_0 \frac{E_s}{E_e}, E_s = \sqrt{4 π / α} m_e c^2 ≈ 21.2 \mathrm{MeV}\]

      对于混合物来说: \(\frac{1}{R_m} = \frac{1}{E_s} ∑ \frac{f_i E_{e i}}{X_i}\)

  • 电磁簇射特征
    • 电磁簇射的纵向分布: 电磁簇射平均能量沉积随着物质层深度变化 (纵向分布):

      \[\frac{\mathrm{d} E}{\mathrm{d} t} = E b \frac{(b t)^{a - 1} e^{- b t}}{Γ(α)}\]

      物质层深度 \(t = \frac{X}{X_0}\) 以辐射长度为单位.

    • 能量沉积最大值 \(t_{\mathrm{max}}\) 处:

      \[t_{\mathrm{max}} = \frac{a - 1}{b} = 1.0 × [ln \frac{E}{E c} + C_i], i = e, γ\]

      其中对于电子 \(C_e = -0.5\), 对于光子 \(C_{γ} = + 0.5\).

    • 电子数目最大值也有上述类似的公式 \(C_e = -1.0, C_{γ} = 0.5\)
    • 电磁簇射的横向分布: 多次库仑散射导致电子偏离簇射轴线, 以及韧致辐射的光子可以偏离簇射轴线较远 (可以见上面的演示的图, 光子 \(γ\) 飞到远处后变成正负电子对)

      电磁簇射横向宽度逐渐展开, 同时能量先增加 (因为级联簇射, 所以电子对/光子数量因为碰撞而增加), 再减弱 (能量损失, 单个粒子能量减弱, 但是宽度变宽). 最终的 \(95\%\) 的粒子沉积在半径 \(∼ 2 R_m\) 圆柱体内.

    • 簇射径迹的总长度: 粒子到达截断能量 \(E_k\) (能够被探测到的最小能量阀值) 前, 粒子走的距离 (可观测径迹长度):

      \[S' = F(ξ) X_0 E / E_e\]

      其中 \(F(ξ) ≈ e^{ξ} [1 + ξ ln (ξ / 1.526)], ξ = \frac{4.58 Z E_K}{A E_e}\). 可观测的次级粒子的径迹总长度随着 \(E_k / E_e\) 增高而减少和入射粒子能量成正比. 于是可以通过该方法来测量入射粒子能量. 理想情况下, 信号和入射能量成正比, 簇射产生的次级粒子数, 或者可以观测的径迹长度的涨落决定本征能量分辨率.

  • 电磁量能器特性参数

    量能器有两种:

    • 全灵敏型 (均匀介质量能器): 均匀介质既是簇射介质, 也是探测器介质.
    • 取样型: 簇射介质和探测器灵敏层堆砌而成.

      (注: 乐, 一开始我想过通过层叠屏蔽和切伦科夫闪烁体来实现能够 测量不同能量的粒子, 但是这个不就是取样型电磁量能器嘛. )

    电磁量能器的性能:

    • 能量分辨率

      \[\frac{σ}{E} = \frac{a}{E} ⊕ \frac{b}{\sqrt{E}} ⊕ c\]

      其中:

      • \(a\) 为噪声项系数, 包含电子学噪声等价能量值以及 代测粒子外的其他粒子沉积涨落.
      • \(b\) 为取样项系数, 包含簇射产生的次级粒子数和各种独立信号产生过程, 以及进一步转换过程的涨落.
      • \(c\) 为常数项系数, 包含能量泄漏的涨落, 量能器之前和量能器内部死区 沉积能量的涨落以及非均匀性和刻度误差等 (量能器本身质量)
      • \(⊕\) 表示等式左边为右边三项的平方和的平方根, 认为这三项是独立的.
      • 本征能量分辨率:
        • 全灵敏量能器
        • 取样量能器
      • 能量泄漏对能量分辨率的影响:
      • 信号产生和收集的非均匀性对能量分辨率的影响
      • 量能器前面和内部物质的死区对能量分辨率的影响
      • 量能器内部刻度误差对能量分辨率的影响
      • 电子学噪声及能量堆积的影响
    • 位置 (空间) 分辨率

      入射位置可以通过如下方式进行测量:

      • 横向能量沉积的重心确定, 精度取决于量能器单元大小 (Moliere 半径), 以及簇射宽度及信号噪声比.
      • 前置簇射探测器 (在 \(≈ 1.5 X_0\) 之后) 量能器之前的探测器测量
      • 量能器取样层 (\(≈ 3 ∼ 5 X_0\))之后的位置探测器
    • 角度分辨率

      \[\frac{δ m}{m} = \frac{1}{2} \sqrt{(\frac{δ E_1}{E_1})^2 + (\frac{δ E_2}{E_2})^2 + (cot \frac{θ}{2} δ θ)^2}\]

    • 时间响应 (响应速度)
    • 双簇射分辨

      在电磁簇射发展初期可以分离.

    • 抗辐照能力

强子量能器

强子相互作用

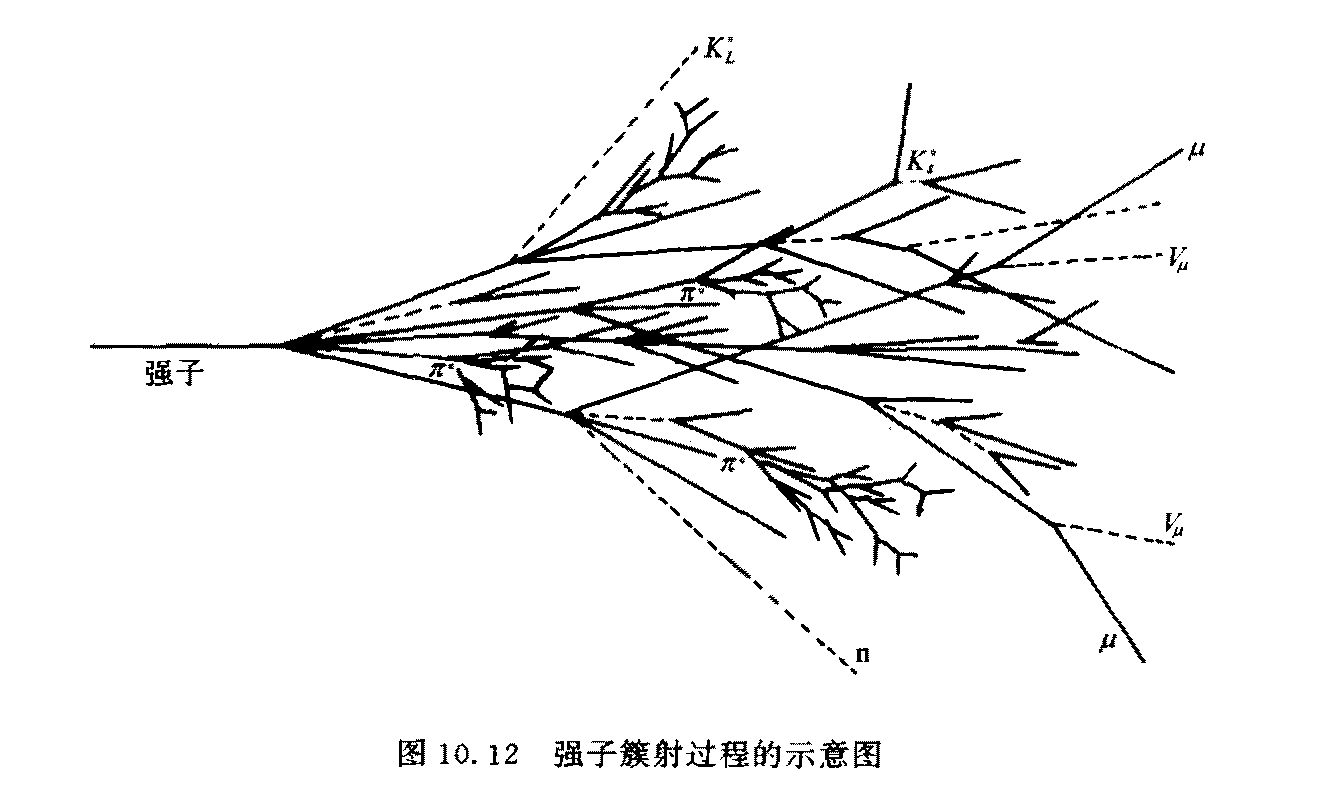
/_img/particles/hadron-shower.png

(因为没有完全的模型, 所以在不同能区有不同的程序处理方式.)

强子量能器的特性

量能器的粒子鉴别

电子 (光子) 和强子的鉴别

通过电子和强子的电磁簇射和强子簇射的纵向发展和横向发展的区别鉴别电子, 强子或者轻子. 一般通过原子序数较大的介质 (\(λ_I\) 和 \(X_0\) 区别大) 进行:

\(μ\) 子鉴别

  • 在纵向精细分割的足够深的量能器中, 通过产生强子簇开始发展前的最小电离长径迹 来鉴别高能 \(μ\) 子.
  • 通过能量横向沉积图像鉴别 \(μ\) 子和强子
  • 判断径迹能否穿过量能器判断是否为 \(μ\).

中微子鉴别

可以测量丢失能量 (missing energy), 丢失动量 (missing momentum) 来间接探测中微子:

  • 丢失能量
  • 横向丢失能量

量能器的结构和信号读出

全灵敏型量能器 (均匀介质量能器)

切伦科夫全吸收量能器

取样量能器

量能器的标定和监测

量能器的标定 (刻度)

量能器的能量信息的刻度方式:

  • 脉冲幅度:

    \[∑_i P_i = K E\]

    其中:

    • \(P_i\) 为第 \(i\) 个灵敏单元的输出信号幅度
    • \(E\) 为入射粒子能量
    • \(K\) 为比例系数

    实验通过量能器对已知能量的束流进行测量, 得到 \(∑ P_i ∼ E\), 然后拟合得到 \(K\).

  • 等效标准粒子:

    比如相对论性 \(μ\) 子在介质中的能量沉积基本与动量无关, 比如在第 \(i\) 个灵敏单元中的能量沉积:

    \[E_i = R_a (\frac{\mathrm{d} E}{\mathrm{d} X})_a ⋅ t_a + R_d (\frac{\mathrm{d} E}{\mathrm{d} X})_d ⋅ t_d\]

    其中:

    • \((\frac{\mathrm{d} E}{\mathrm{d} X})_a\) 和 \((\frac{\mathrm{d} E}{\mathrm{d} X})_d\) 分别为 \(μ\) 子在吸收介质和探测器介质的能损
    • \(t_a\) 和 \(t_d\) 分别为吸收介质和探测器介质的厚度
    • \(R_a\) 和 \(R_d\) 为对应的权重因子 (对于 EM 量能器 \(R_a ≈ R_d ≈ 1\))

    于是对于第 \(i\) 个单元通过时输出的信号幅度 \(P_{μ i}\), 于是在入射粒子在单元中沉积的能量: \((\frac{P_i}{P_{μ i}}) ⋅ E_i\). (但是一般只能用来进行近似估算)

量能器的监测

  • 闪烁体量能器的监测系统
  • 气体量能器的监测系统

读出电子学与在线数据获取

/_img/particles/data-reading-system.svg

粒子物理实验在线数据获取的电子学仪器总线系统

在广义上来说, 总线就是一组其功能被明确定义的公共连线, 由它来完成外设与计算机, 外设与外设, 或仪器与仪器之间的信息传送. 一般, 它们是传送数字量信息, 包括数据, 控制信号和状态信息的传送, 在总线中也包含有电源线.

常用总线系统:

  • CAMAC (Computer Automated Measurement and Control) 系统

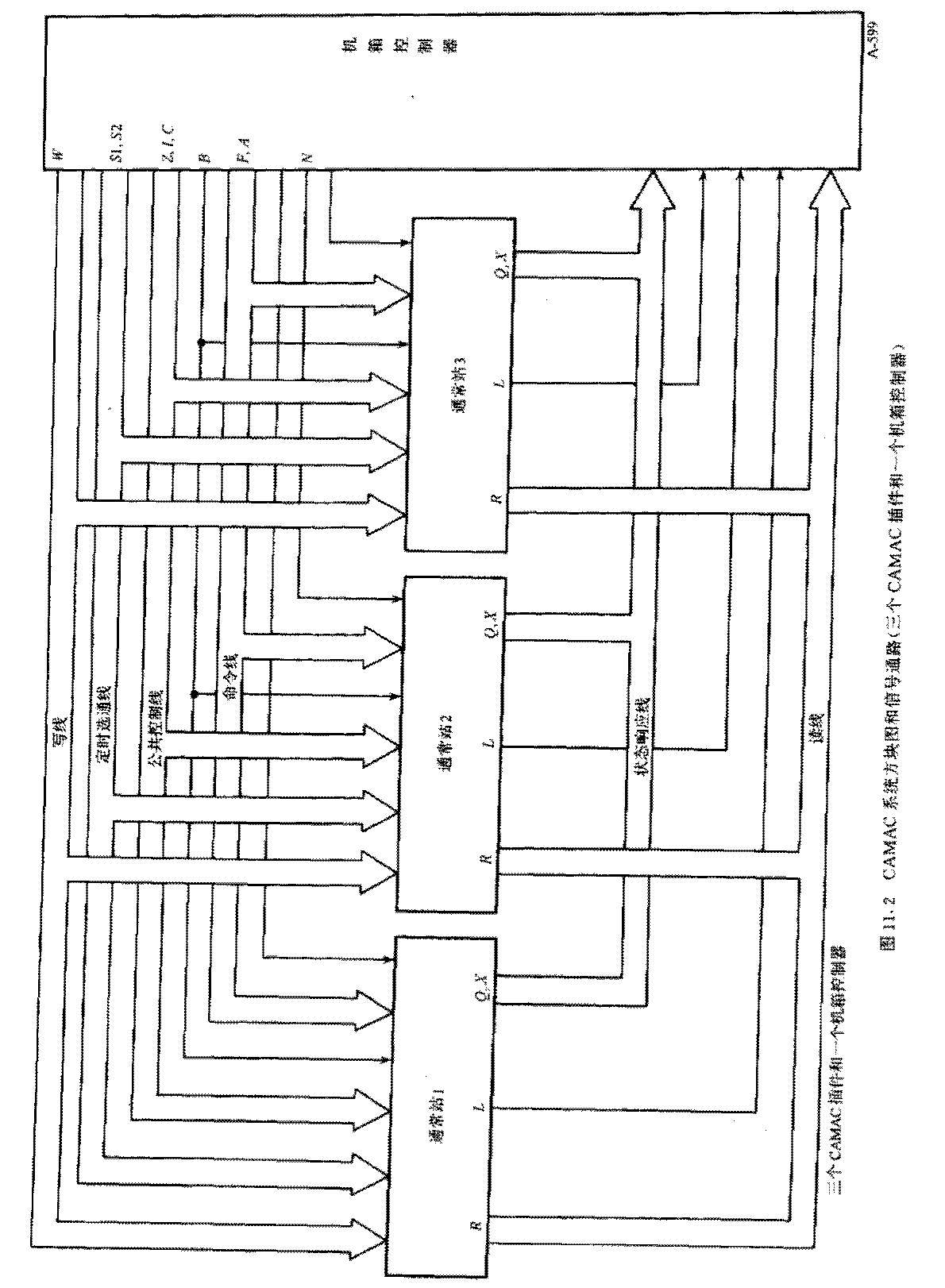
    /_img/particles/camac-bus-line.png

    主要特性为标准模块式仪器总线系统:

    • 标准机箱 (\(482.6 × 221.5 × 360 ∼ 525 \mathrm{mm}\), 深度受电源影响) 有 25 个站 (从左到右 \(1 → 25\)), 1 到 24 为普通站, 25 为控制站 (一般宽度为二, 会占用 24).
    • 并行总线 CAMAC 系统中最多并接 7 台机箱, 串行总线中最多接 62 台.
    • 机箱背部为数据通道 (DATAWAY 86 芯插座), 包含读, 写, 控制, 状态, 寻址信息, 以及供电电源和专用线.

      控制站和普通站之间有专用连线:

      1. N 线 (站号线), 控制站通过该线对普通站进行寻址
      2. L 线 (LAM 线), 普通站通过 L 线请求控制站的注意

      操作命令的组成:

      1. 寻址信号 N: 规定参与该操作的插件 (单个或者多个)
      2. 子地址总线上的信号:
    • 功能插件 (\(H=221.5 \mathrm{mm}, W = (17.2 s_{=1, 2, 3} - 0.2), (17.2 s_{4 ∼ 25} - 0.4) \mathrm{mm}\), \(s\) 为插件占用站的数目, 常见的插件宽度 (\(s\)) 为单宽或者双宽, 深度 \(305 \mathrm{mm}\)) 是插拔式的, 可以在标准机箱上插拔替换.

      功能插件对应一个标准的机箱数据通道, 并且和计算机和功能无关.

    • 机箱电源: 电压容差, 电流负载能力 (机箱数据通道插座上的接点电流 \(\leq 3 \mathrm{A}\)), 一个机箱总功率 \(\leq 200 \mathrm{W}\) (无强制通风), 每单宽功率 \(\leq 8 \mathrm{W}, 25 \mathrm{W}\).

前端电子学

前端电子学干的事情:

  • 将读取的信号转换为数据的操作, 电信号特征 \(→\) 粒子特性数据.
  • 与触发和在线计算机连锁, 有序记录事例
  • 提供触发条件

信号处理基本方法

(注: 这一段因为没有太多的模电知识, 可能全都是在抄书. 虽然其他也差不多)

电荷测量

一般做法就是电荷 \(\overset{\mathrm{QAC}}{→}\) 电压 \(\overset{ADC}{→}\) 数字量

  1. 电荷电压变换 (QAC)

    让探测器输出电流 \(i\) 对固定电容 \(C\) 充电进行电荷电压转换 \(U = \frac{Q}{C} = \frac{∫ i \mathrm{d}t}{C}\):

    • 电荷灵敏放大器

      \[V_o = \frac{Q_i}{C_f}\]

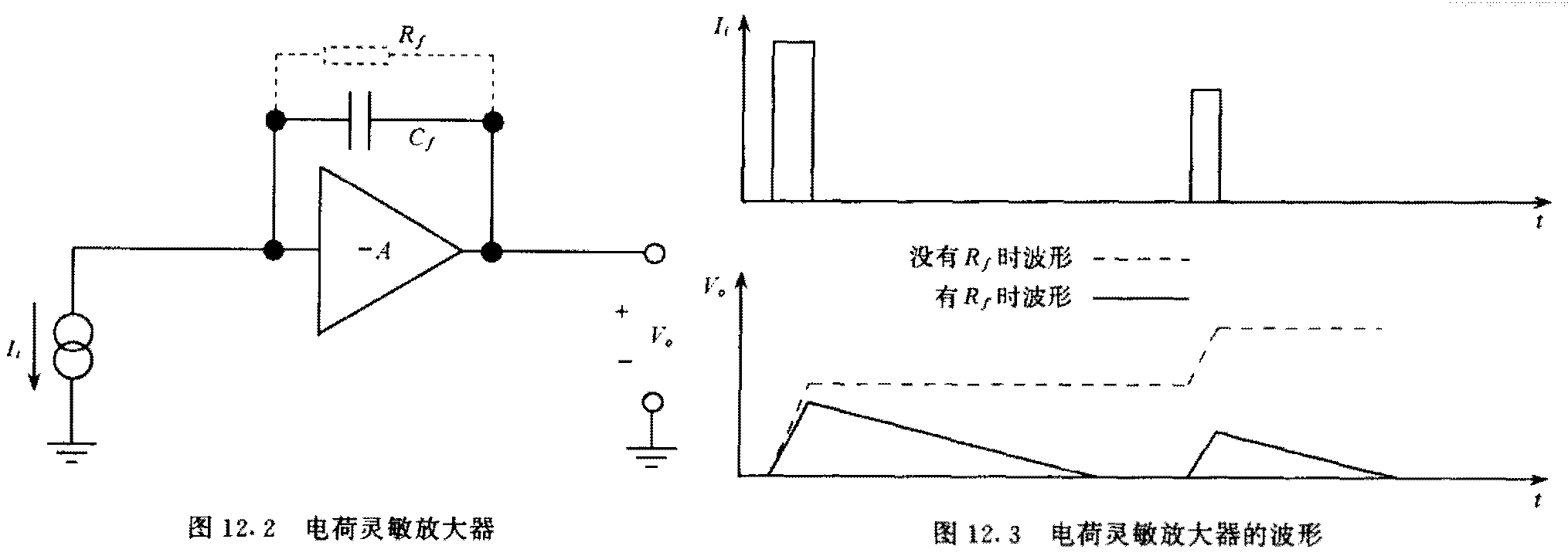
      /_img/particles/charge-sensitive-amplifier.png

    • 电压灵敏放大器

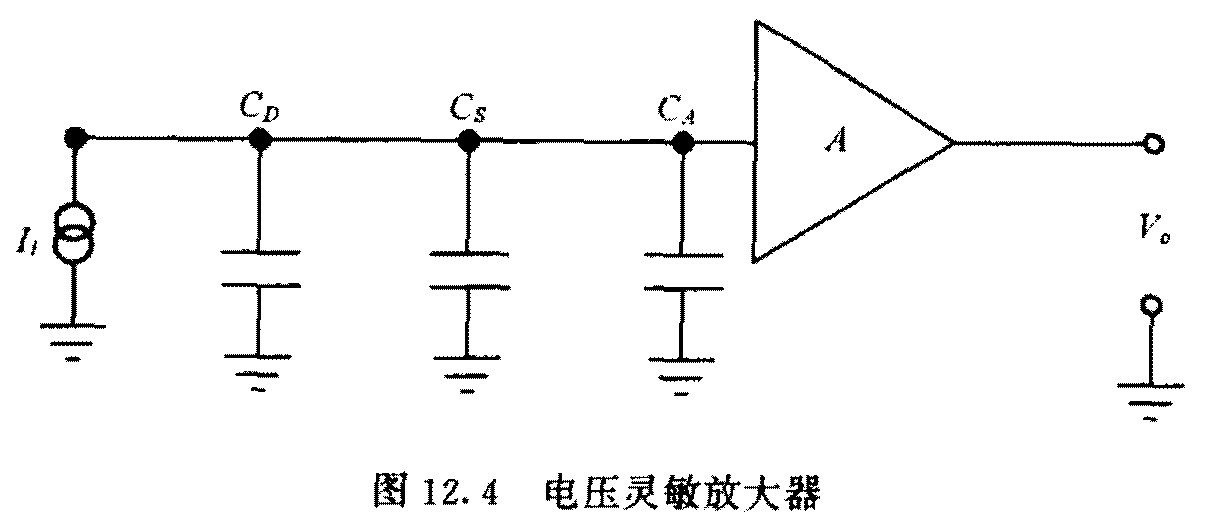
      /_img/particles/voltage-sensitive-amplifier.png

    • 电流灵敏放大器
  2. 模拟数字变换 (ADC)
    • FADC (Flash ADC):
    • 逐次比较法 ADC:
    • 分级 FADC:
  3. 电荷时间变换 (QTC)

时间测量

测量探测器输出信号的出现时间 (指针对某一个参考信号的时间间隔). 干的事情如下:

  1. 定时甄别电路确定信号的出现时刻

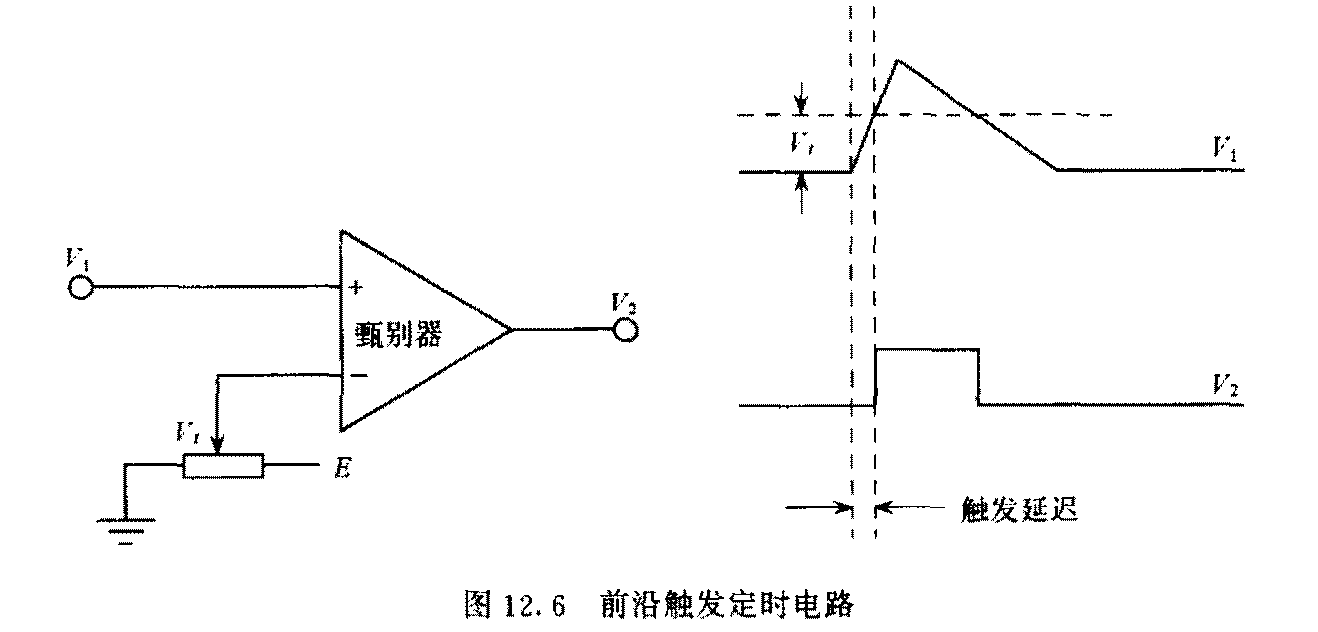
    /_img/particles/front-trigger-timeing-circuit.png

    因为信号会有一个上升时间, 所以通过探测信号上升沿来确定电压信号的出现时间. 通过一个电压比较器和阈值 \(V_t\) (比较器 - 节点的那个输入) 进行判断.

    • 关于噪声的影响:

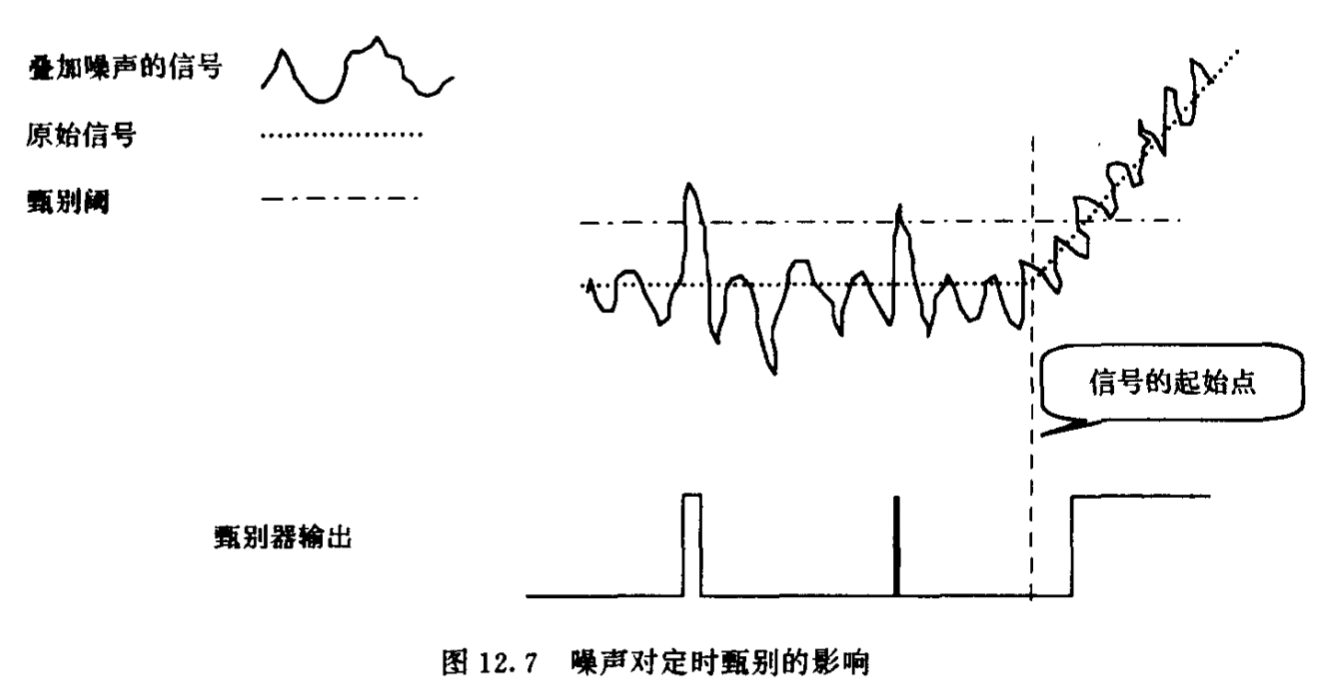
      /_img/particles/noise-on-front-trigger-circuit.png

      过小的阈值会导致产生毛刺信号. 过高的阀值可能会带来更大的时间差. 假如时间差是定值还可以修正, 但是信号往往是随机变化的, 所以没法消除时间游动.

    • 恒比定时, 用来减少时间游动的一种方法.

      假设定时甄别的甄别阈和信号幅度成正比: \(V_T = p A\). 于是定时点 \(A F(t) = p A ⇒ F(t) = p\) 仅和波形有关, 可以用来消除幅度变化造成的时间游动.

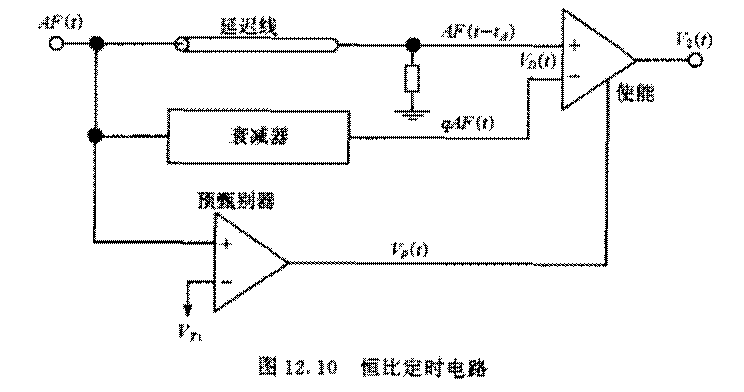
      /_img/particles/constant-time-circuit.png

    • 关于过零信号 (双向信号):

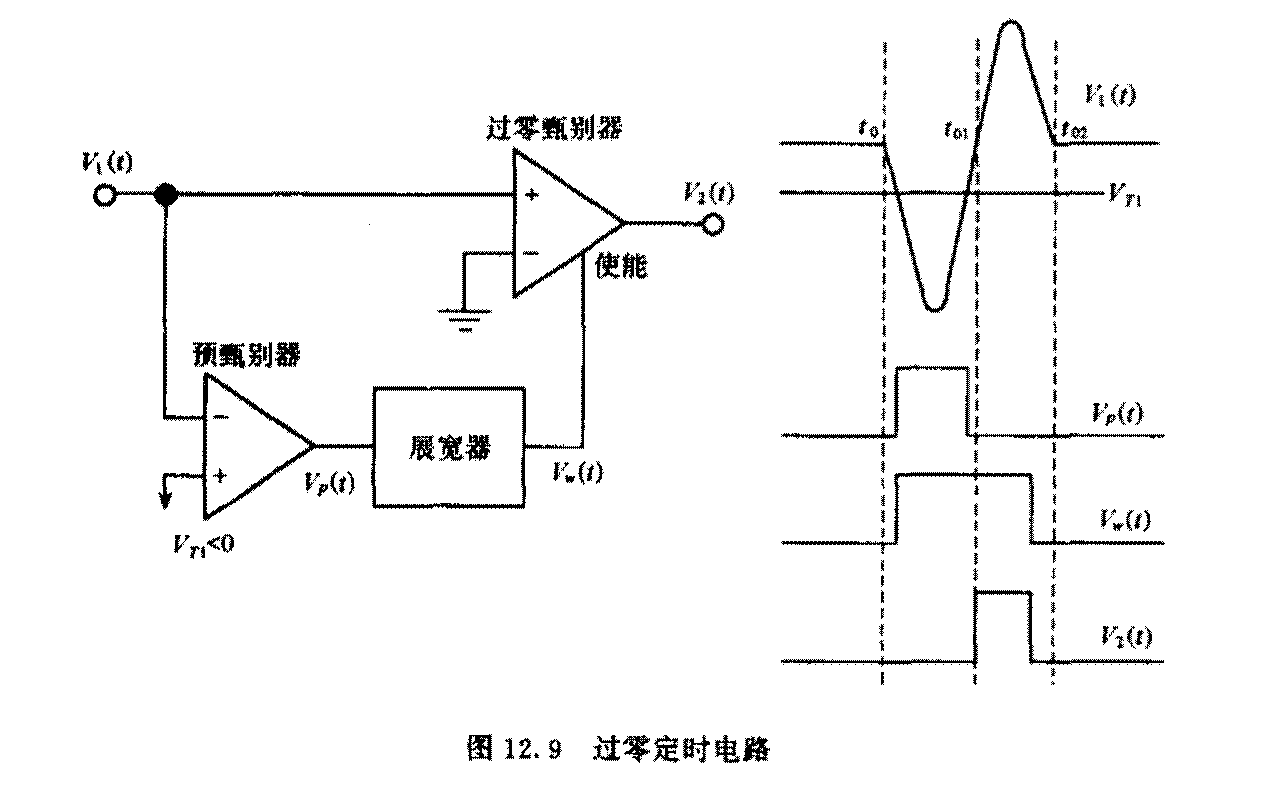
      /_img/particles/zero-signal-circuit.png

      假设信号 \(AF(t)\) ( \(A\) 为幅度系数), 因为信号零点 (\(AF(t) = 0 ⇒ t_0, t_{01}\)) 之间的时间差和幅度无关, 可以作为测量依据 (过零定时).

      需要信号有一个过零点, 定时器阈值为零, 并且还要消除基线上的噪声误触发.

  2. 时间数字变换电路 (TDC) 将被测信号和参考信号的时间间隔变成数字数据

    定时甄别电路得到待测信号 (Start 信号) 和参考信号 (Stop 信号), 通过 TDC 将 Start 和 Stop 之间的时间差转换为数码, 然后用计算机读出.

    转换方式有:

    • 计数式时间数字转换: 用振荡器来振荡, 缺点就是在小时间间隔需要高频振荡器.
    • 带游标的计数式时间数字变换: 一组振荡器之间相差一定的时间间隔, 比如周期 \(10 \mathrm{ns}\) 的振荡器, 每个间隔时间 \(1 \mathrm{ns}\). (通过多个带延时单元的环形振荡器 或者延迟线锁相环来实现, 并且延时时间通过电压控制).
    • 时间振幅变换 (TAC): 用恒流源对电容充电实现的时间幅度变换. \(U = \frac{I × t}{C}\) (需要保证结束后将电容放电).

击中信息获取

只需要关心是否击中即可, 信号就是 “是” 和 “否” 两个信息.

波形取样技术

将探测器输出的电流信号经过电流到电压的变换器 (电阻? 应该没有那么 low 吧), 可以得到和输入电流成正比的电压信号. 将电压采样并数字化, 可以得到波形的采样数据. 根据波形拟合, 可以用来判断和区分信号对应的粒子种类.

一般需要 FADC (数据量大) 及分布式高速微处理器 (比如 DSP). 并且还需要解决如何在较低的采样率, 来得到较高的计算精度.

噪声处理

  • 噪声对测量的影响
    • 无法测量到信号电压的准确值 (噪声的均方值影响分辨率)
    • 无法进行准确的定时甄别 (噪声的均方值 \(V_n\) 引入的定时误差均方值 \(t_n = \frac{V_n}{p}\))
    • 用幅度甄别确定探测器是否击中时, 在阈值较低时因为噪声误触产生击中假象, (但是阈值较高又容易导致漏判)

    如何看到噪声 (bushi), 在高级示波器上可以看到信号中间亮, 上下暗淡

  • 噪声特性以及分析方法

    认为电噪声服从高斯正态分布, 使用均方根 \(σ\) 来表征噪声强度 (\(σ\) 越大, 信号离散性越大). 信号的均方值通过信号的功率谱密度函数在频域积分表征, 通过噪声频谱来求噪声均方值.

    1. 时域中噪声瞬时值平方平均值
    2. 噪声概率密度函数均方值
    3. 频域中噪声功率谱密度函数在整个频率域内的积分
  • 减少噪声影响的方法

    电子学电路来源主要有: 探测器和前端电子学电路部分, 因为信号逐级放大, 所以前级电路的噪声更为主要: 使用低噪声元件, 低噪声电路 (电荷灵敏放大器信噪比 就比电压灵敏放大器高), 降低电路工作点 (适当降低电源电压和器件工作电流可以 通过降低工作电流来减少第一级电路的噪声), 降低工作温度 (低温浸泡), 冷端接技术 (适用于长距离的电缆连接, 需要放大器 (等效) 输入阻抗和 电缆特性阻抗匹配, 放大器输入阻抗噪声等效于低温电阻).

信号堆积问题

假如两个信号时间间隔太近, 小于信号宽度时, 就会导致两个信号混在一起, 无法区分. 方法就是减少信号宽度.

数据预处理

  • 数据 (幅度 (电荷) 数据, 时间数据, 是否击中数据 + 探测器单元地址码) 压缩
  • 数据归一化

前端电子学读出

  • 模拟多路器
  • 数字多路器
  • 流水线技术
  • 事例暂存技术
  • 高速光缆技术

前端电子学自检和校准

通过在线故障监测系统来随时监测问题并确定故障部位. 使用可变元件来调整精度的话, 会降低系统的稳定性和可靠性, 就会导致需要经常维护; 使用软件方法随时测量并计算系统台阶, 增益和非线性, 得到系统校准数据, 使用其可以用来对测量数据归一化得到更加精确的测量结果.

除了前端电子学以外, 还要: 幅度或者时间延迟可以精确控制的信号产生器, 可以将信号加到每一路前端电子学的输入端; 可以协调信号产生器, 前端电子学 以及计算机运行的时序控制器.

标准信号的获得

两种获得标准信号的方法:

  • 将一个电压脉冲通过一个电容接到通道的输入端: \(Q = U C\). 假如通道的输入电阻为 \(R\), 则通道输入的电流信号为一个指数衰减波形.

    只要时间常数比通道的电荷搜集时间短, 电压脉冲的宽度比通道的电荷搜集时间长, 精确控制 \(R\) 和 \(C\) 可以获得标准的电荷, 通过精密延迟电路精确控制电压脉冲的起始时刻可以获得标准的时间.

    优点是标准电荷和标准时间与通道的输入阻抗无关, 缺点是指数衰减波形的持续时间较长, 有些场合不合适.

  • 将电压脉冲直接加到通道的输入端, 假设输入阻抗为纯电阻 \(Q = U T / R\)

    精确控制 \(U, T, R\), 可以获得标准电荷, 通过精密延迟电路精确控制电压脉冲起始时刻 可以得到标准时间. (但是不容易控制脉冲宽度 \(T\), 对电荷灵敏放大器等不适用).

校准

  • 电荷通道

    \[Q = α_q (D_q - δ_q) + β_q (D_q - δ_q)^2 + γ_q(D_q - δ_q)^3 + \cdots\]

    电荷通道校准任务既是在忽略高次项 (\(γ_q, \cdots\)) 后的其他系数 (最小二乘法拟合).

  • 时间通道

    \[T = α_t (D_t - δ_t) + β_t (D_t - δ_t)^2 + \cdots\]

系统干扰及其治理

  • 电源干扰:
    • 减少电源稳压滤波: 退耦滤波电路, 滤波电容 (低通滤波器) 可以去掉高频部分, 低频部分可以通过稳压电源或者三端稳压块减少. 在机箱插件电路中, 加入独立的滤波电路, 减少机箱插件里面的线路的干扰.
    • 减少线路对电源干扰敏感性: 比如差动放大器, 深度负反馈放大器
  • 电磁场干扰:

    金属屏蔽 (\(U_E = E D\)), 扭绞线 (\(U_B = - \frac{\mathrm{d} (B D L)}{\mathrm{d} t}\)), 扁带电缆传送信号可以采用一信一地 (一个信号线, 一个下地线, 抵销干扰). 同轴电缆可以屏蔽和导体垂直的电磁场, 但是平行电场会在外导体上感应电压, 引入干扰.

    最好采用带屏蔽的扭绞电缆传送小信号.

  • 地电流干扰:

    信号通过公共地线相互干扰.

    • 单点接地
    • 前置放大器
    • 大地面
    • 差动信号传输方法
    • 光耦合
  • 同步抗干扰
  • 缩短模拟部分电缆长度

触发判选和数据获取系统

触发判选的作用: 一个能够剔除本底, 挑出有用信号的系统. 设计取决于:

  • 探测器以及读出电子学的具体结构
  • 加速器的时间结构:
  • 事例率和触发率
    • 亮度 \(L\) (度量实验的灵敏度): 反应截面为 \(1 \mathrm{cm}^2\) 时每秒的事例数. 在固定靶实验里面, 亮度是单位面积内靶原子数和束流流强的乘积.
    • 好事例率: \(n_{ph} = σ L\), \(σ\) 为研究物理过程的作用截面.
    • 本底事例率:
      • 宇宙线本底

        扔到深深的矿井里面, 隧道里面, 冰层, 水下等 (土法吸收宇宙线).

      • 丢失束流粒子本底

        丢失电子特征: 从束流轴出发, \(Z\) 方向分散, 多为小角度散射, 每次只有一个粒子.

        • 横动量选择 (利用库仑散射微分截面选择)
        • \(Z\) 方向选择
      • 电子学噪声造成的假事例的排除

        假事例表现为 (单事例中) 成片着火, 会导致事例重建失败.

      • 同步辐射造成的本底
      • 其他本底
      • 不感兴趣物理事例本底
  • 数据量
  • 实验目的

死时间 \(τ\): 假如一个事例通过触发判选, 开始模数变换 (至此开始前端电子学无法接受探测器信号), 变换结束后给出中断信号, 然后让数据获取系统根据中断信号读出数据并处理, 然后放出还原信号 (这个时候, 前端电子学可以开始继续接受探测器信号了). 而这段时间, 就是死时间.

假设实际发生并且应该被记录的事例率 \(n_o = ε_{ph} × n_{ph} + ε_{bg} × n_{bg} + ε_{cr} × n_{cr}\), 其中 \(ε_{ph}\) 为好事例 (除了它, 其他越小越好), \(ε_{bg}\) 束流本底, \(ε_{cr}\) 宇宙线本底的触发效率. 但是实际处理了 \(n\) 个事例, 总的死时间 \(n τ\), 总共损失了 \(n_o × n τ\) 个事例, 损失了亮度 \(Δ L = n τ L\), 计算截面 (要用有效亮度) \(σ = \frac{n}{L_{\mathrm{eff}}}\).

解决方法:

  1. 改进触发判选减少 \(ε_{bg}\) 和 \(ε_{cr}\) 来减少 \(n_0\)
  2. 加快数据获取系统速度或者压缩数据量来减少 \(τ\)
  3. 使用缓冲存储器

触发判选系统

触发判选系统要求:

  • 对好事例判选效率高
  • 尽可能多地排除本底
  • 判选速度块
  • 灵活可变

多级触发

第一级触发用简单触发条件 (主打一个你就说快不快吧), 第二级触发用较长的时间进行较长时间的一个筛选 (降低事例率), 最后是第三级触发 (交给数据获取系统).

高亮度下的触发判选

触发判选系统性能

  • 每个事例读出信息和直方图
  • 判选过程中各种计数率和监测定标器
  • 触发效率测量

数据获取系统

  • 电子学刻度和记档
  • 运行时初始化, 前端各微处理器加载, 各状态控制寄存器设置
  • 从前端电子学读数
  • 数据的预处理和装配
  • 全事例数据的重建分析 (在线事例筛选, 即第三级触发)
  • 数据的记录
  • 探测器运行情况的监测 (抽样分析事例, 建立各种直方图并作单事例和直方图显示)
  • 运行的操作控制, 如键盘命令输入, 接触屏幕输入和鼠标输入等
  • 运行条件的显示和记档 (如运行 RUN 号, 磁带号, 加速器能量和亮度, 环境和高压监测等, 有时把该条和上一条称为 slow control)
  • 错误显示, 报警和记档
  • 磁带或磁盘上记录的数据的回读及处理

死时间减少

  • 较快总线
  • 压缩数据
  • 多个智能控制器并行读出
  • 各级添加缓冲存储器
  • 存储器直接访问 (DMA) 或者数据块传输 (block transfer)
  • 嵌入式单板机和实时操作系统代替集中式多用户多进程的主机, 加快中断响应.

The End

这个, 感觉基本都在抄书, 虽然看完之后确实有点感觉, 但是也只是有点感觉. 电路部分没有跑过有点虚, 物理部分感觉不超过我原子物理课教的内容 (? 飘了是吧) 其他都是有点朦朦胧胧的感觉, 估计搬砖之后可以有点感觉.

之后再更新.

Plotting

为了能够更好地输出图片, 这里做了一些小小的措施:

Gnuplot

<<gnuplot-light>>

reset

set key tc rgb 'grey'
set xlabel 'X' tc rgb 'grey'
set ylabel 'Y' tc rgb 'grey'
set border lw 1 lc rgb 'grey'

set linetype 1 lw 2 lc rgb 'grey'
set linetype 2 lw 2 lc rgb 'grey'
set linetype 3 lw 2 lc rgb 'grey'
set linetype 4 lw 2 lc rgb 'grey'
set linetype 5 lw 2 lc rgb 'grey'
set linetype 6 lw 2 lc rgb 'grey'
set linetype 7 lw 2 lc rgb 'grey'
set linetype 8 lw 2 lc rgb 'grey'

reset

set key tc rgb 'black'
set xlabel 'X' tc rgb 'black'
set ylabel 'Y' tc rgb 'black'
set border lw 1 lc rgb 'black'

set linetype 1 lw 2 lc rgb 'black'
set linetype 2 lw 2 lc rgb 'black'
set linetype 3 lw 2 lc rgb 'black'
set linetype 4 lw 2 lc rgb 'black'
set linetype 5 lw 2 lc rgb 'black'
set linetype 6 lw 2 lc rgb 'black'
set linetype 7 lw 2 lc rgb 'black'
set linetype 8 lw 2 lc rgb 'black'

Graphviz

<<graphviz-light>>

bgcolor="transparent"; fontname="Arial";
node [fontname="Arial"];
edge [fontname="Arial"];

color=lightgrey; fontcolor=lightgrey;
edge [color=lightgrey, fontcolor=lightgrey];
node [color=lightgrey, fontcolor=lightgrey];