Metropolis Hastings Algorithm
About
软物质物理课里面讲到的一个 Monte Caro 模拟算法, 感觉比较有意思.
免责声明: 这玩意我写的不一定对, 估计里面有一堆的 bug.
Metropolis Hastings Algorithm
解决的问题
物理量计算困难
对于物理量的平均:
\[\left\langle A \right\rangle = \frac{1}{Z} ∫ A(\boldsymbol{R}^N) e^{- β U(\boldsymbol{R}^N)} \mathrm{d}\boldsymbol{R}^N\]
发现积分不是很好积分, 于是将问题变换为随机采样: 找一个描述分布的概率函数 \(\left\{ \boldsymbol{R}^N_i \right\} → ρ(\boldsymbol{R}^N)\), 于是可以有:
\[\left\langle A \right\rangle ≈ \frac{1}{M} ∑_i A(\boldsymbol{R}^N_i) \frac{e^{- β U(\boldsymbol{R}^N_i)}}{Z ρ(\boldsymbol{R}^N_i)}\]
数学的说法
可以去找找看 Monte Carlo Integratoin:
- 对于 \(Ω ⊂ \boldsymbol{R}^m\) 上的积分 \(I = ∫_{Ω} f(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}\)
- 在 \(Ω\) 上取随机采样点: \(\left\{ \boldsymbol{x}_1, \cdots, \boldsymbol{x}_N \right\} ∈ Ω\)
- 用求和代替积分: \(I \overset{N → ∞}{≈} Q_N = \frac{V}{N} ∑_{i=1}^N f(\boldsymbol{x}_i) = V \left\langle f \right\rangle\). 其中 \(V = ∫_{Ω} \mathrm{d} \boldsymbol{x}\) 为 \(Ω\) 的体积.
算法
通过 Markov 链进行采样: \(X^1 → \cdots → X^m → X^{m+1} → \cdots → X^{m + M}\). 具体的做法如下:
- 选择一个初始状态
- 计算一个随机游走, 得到下一个可能的状态:
- 计算下一个状态可能存在的概率
- 若存在, 则将该状态记录, 并重复 2 步骤
- 若不存在, 则重新生成
(defun importance-sampling (state gen acc samples &optional (burn-in 0))
"使用 Markov 链进行采样: 初始状态 `state', 下一个状态函数 `gen', 判断函数 `acc', 采样数 `samples', 初始抛弃 `burn-in' 个样本.
返回状态列表."
(when (not (zerop samples)) ; 若仍然需要进行采样
(let ((candidate (funcall gen state)))
;; 若不接受, 则重新生成
(loop while (not (funcall acc candidate state)) do
(setf candidate (funcall gen state)))
;; 抛弃前 burn-in 个状态, 记录 samples 个状态
(if (zerop burn-in)
(cons state (importance-sampling candidate gen acc (1- samples)))
(importance-sampling candidate gen acc samples (1- burn-in))))))
循环版本的代码
(defun sampling (init gen acc samples &optional (burn-in 0))
"使用 Markov 链进行采样: 初始状态 `state', 下一个状态函数 `gen', 判断函数 `acc', 采样数 `samples', 初始抛弃 `burn-in' 个样本.
返回状态列表."
(let ((state init)
(candidate (funcall gen init)))
(labels ((update () ; 采样
(loop do (setf candidate (funcall gen state))
while (not (funcall acc candidate state)))
(setf state candidate)))
;; 抛弃前 burn-in 个状态
(loop for - below burn-in do (update))
;; 收集后 samples 个状态
(loop for - below samples do (update)
collect candidate))))
注: 这里建议还是使用循环版本的代码.
一些例子
一维势场中游走
- 随机往正/负方向行走一定的距离:
(defun 1-d-gen (state) "随机往正方向或者负方向行走 [0,1) 的距离." (let ((sign (- 1 (* 2 (random 2)))) (len (random 1.0))) (+ state (* sign len))))
- 认为势场 \(U = (x - 3)^2 (x + 10)^2\):
(defun 1-d-U (state) "U(x) = (x - 3)^2 (x + 10)^2" (* (expt (- state 3) 2) (expt (+ state 10) 2)))
- 判断函数如下:
- \(\mathrm{d}E = U(s') - U(s)\)
- 若 \(\mathrm{d}E < 0\), 则允许
- 若 \(\mathrm{d}E > 0\), 则以概率 \(min \left\{ 1, e^{- \frac{\mathrm{d}E}{k T}} \right\}\) 进行判断
(defun 1-d-acc (state2 state1) "从 state1 变成 state2 是否接受." (let ((dE (- (1-d-U state2) (1-d-U state1))) (kT 300)) ; 瞎取的数 (or (< dE 0) (< (random 1.0) (exp (- (/ dE kT)))))))
- 于是一个可能的模拟如下:
(importance-sampling 0 #'1-d-gen #'1-d-acc 10000 50)
注: 大概感觉是这样, 实际上代码还要一些修改 (手动写成循环形式). 为了方便, 我将其转写成 Mathematica 的代码:
Sampling[init_, genF_, accF_, samples_, burnIn_] :=
Module[{state = init, candidate = genF[init]},
(*去掉前面 burnIn 个采样点*)
Do[Until[accF[candidate, state], candidate = genF[state]], burnIn]; state = candidate;
(*记录 samples 个采样点*)
Table[Until[accF[candidate, state], candidate = genF[state]]; state = candidate, samples]];
oneDU[state_] := (state - 3)^2*(state + 10)^2;
oneDGen[state_] := RandomReal[{-1, 1}] + state;
oneDAcc[state2_, state1_] :=
With[{dE = oneDU[state2] - oneDU[state1], kT = 300},
Or[dE < 0, RandomReal[] < Exp[-dE/kT]]];
最终的效果如下:
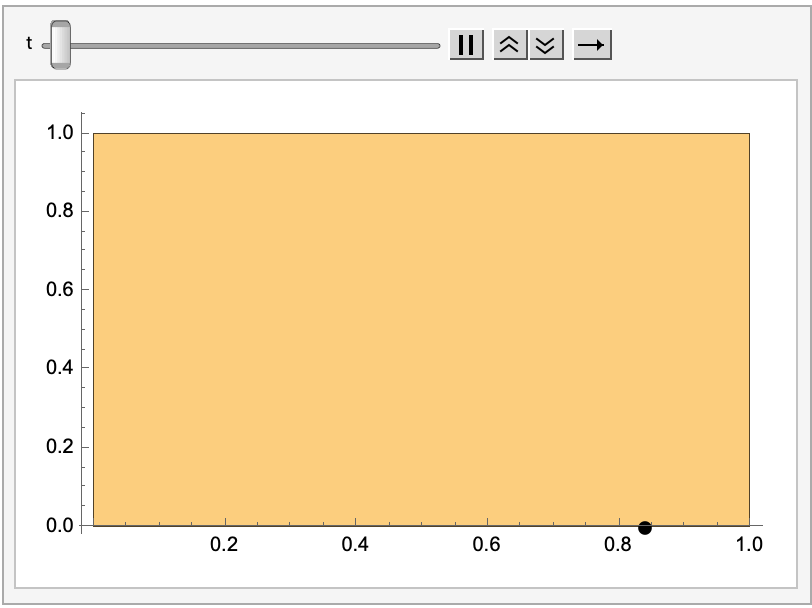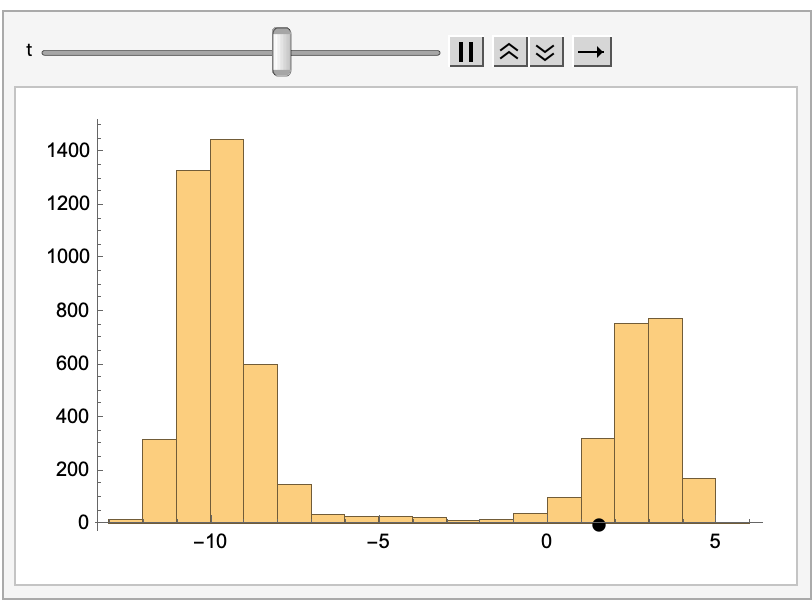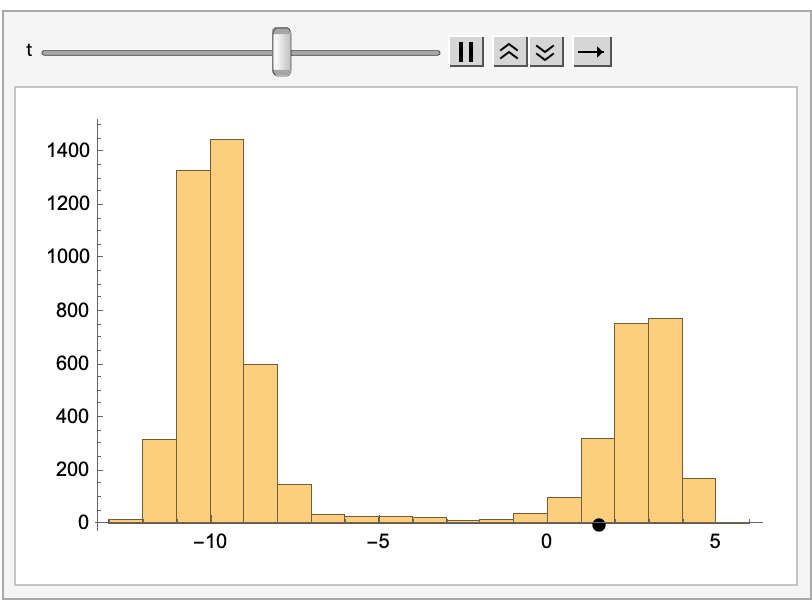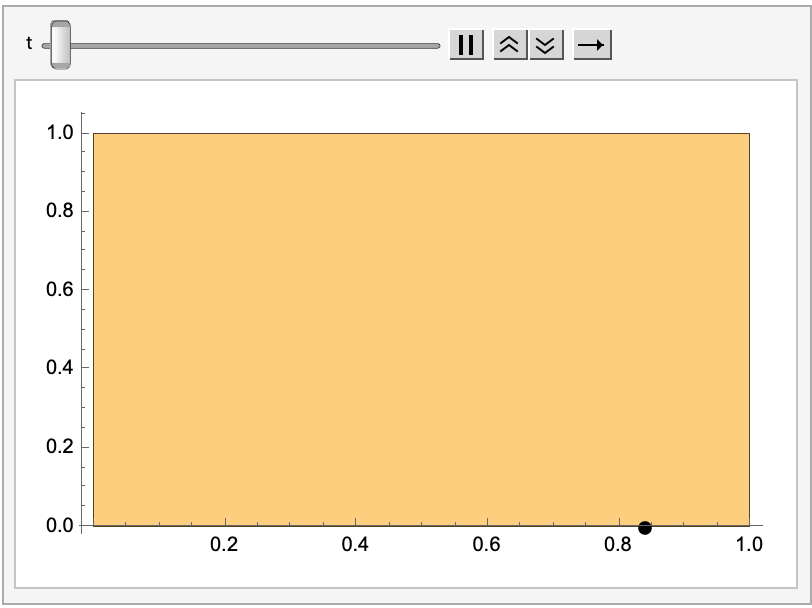
(使用 Mathematica 导出, Mathematica 的代码可以在此下载: metropolis.nb).
关于速度和优雅的问题
我承认我的代码写得很狗屎. 所以请不要用速度和优雅程度来评判我.
更早一版的代码更加烂:
ImportanceSampling[init_, genF_, accF_, samples_, burnIn_] :=
Module[{
samplesC = samples,
burnInC = burnIn,
states = {},
state = init,
candidate},
While[samplesC > 0,
candidate = genF[state];
While[Not[accF[candidate, state]], candidate = genF[state]];
AppendTo[states, candidate];
state = candidate;
If[burnInC > 0, burnInC--, samplesC--]];
states];
对于两个规模在 10000 的代码:
Timing[Sampling[0, oneDGen, oneDAcc, 100000, 100];] (* {0.888991, Null} *)
Timing[ImportanceSampling[0, oneDGen, oneDAcc, 100000, 100];] (* {9.30457, Null} *)
注: 不过怎么说呢, Mathematica 的性能和其他的比起来可能还是差了一些吧…
METROPOLIS> (time (sampling 0 #'1-d-gen #'1-d-acc 1000000 50)) Evaluation took: 0.156 seconds of real time 0.156800 seconds of total run time (0.151595 user, 0.005205 system) [ Real times consist of 0.007 seconds GC time, and 0.149 seconds non-GC time. ] [ Run times consist of 0.007 seconds GC time, and 0.150 seconds non-GC time. ] 100.64% CPU 15,986,880 bytes consed
并且这个 Lisp 代码还是没有优化的那种呢…
当然, 估计和 C 还有 C++ 比起来的话, 肯定还是有点距离的. 但是至少和 C 比起来, 我稍微更加熟练这类型的写码风格吧.
对程序进行一些修改
在写程序的时候发现了一个问题, 貌似我并不关心中间采样的东西究竟长什么样, 因为我只关心最终的分布是什么样的. 所以稍微修改一下程序:
(defun sampling-hist (init gen acc samples burn-in yield)
"使用 Markov 链进行采样:
+ 初始状态 `init
+ 下一个状态函数 `gen'
+ 判断函数 `acc'
+ 直方图函数 `hist'.
+ 采样数 `samples'
+ 初始抛弃 `burn-in' 个样本
+ 取样判断函数 `yield"
(let ((state init)
(candidate (funcall gen init)))
(labels ((update () ; 采样
(loop do (setf candidate (funcall gen state))
while (not (funcall acc candidate state)))
(setf state candidate)))
;; 抛弃前 burn-in 个状态
(loop for - below burn-in do (update))
;; 收集后 samples 个状态
(loop for - below samples do (update)
do (funcall yield candidate)))))
一些 “作弊” 内容
为了简单处理问题, 以及我不会写直方图统计代码, 所以我决定直接调用库: GSLL.
虽然原则上使用 CFFI 来直接调用 GSL, 但是对于已经写好了的东西我觉得还是直接拿来最好. :)
(let ((hist (make-histogram 100))
(min 0)
(bin 100)
(binsize 1))
(defun 1-d-read-hist ()
(loop for i below bin
collect (grid:aref hist i)))
(defun 1-d-integrate (func)
(/ (loop for i below bin
for n from min by binsize
collect (* (funcall func n)
(grid:aref hist i))
into f
finally (return (apply #'+ f)))
(sum hist)))
(defun 1-d-hist-set-range (x-min x-max)
(set-ranges-uniform hist
(coerce x-min 'double-float)
(coerce x-max 'double-float)))
(defun 1-d-renew-hist (bin-num x-min x-max)
(setf hist (make-histogram bin-num)
min x-min
bin bin-num
binsize (/ (* 1.0 (- x-max x-min)) bin-num))
(1-d-hist-set-range x-min x-max))
(defun 1-d-hist (sample)
(increment hist (coerce sample 'double-float)))
(defun draw-hist (output)
(eazy-gnuplot:with-plots (s :debug NIL)
(eazy-gnuplot:gp-setup :output output
:terminal :png)
(eazy-gnuplot:plot
(lambda ()
(loop for i below bin
for n from min by binsize do
(let ((value (grid:aref hist i)))
(format s "~&~a ~a" n value))))
:with '(:boxes)
:notitle NIL))
output))
以及一些简单的绘图程序, 使用的是 eazy-gnuplot.
那么修改后的一维势场游走模型如下:
(defun 1-d-sim (output &key (x-min -20) (x-max 20) (bin 50)
(sample 10000) (burn-in 100))
(1-d-renew-hist bin x-min x-max)
(sampling-hist 0 #'1-d-gen #'1-d-acc sample burn-in #'1-d-hist)
(draw-hist output)
output)
绘制得到的结果如下:
(1-d-sim output)
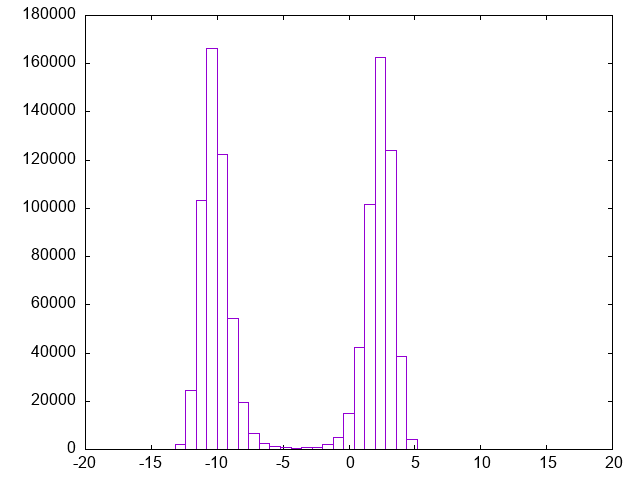
注: 之所以隐藏, 除了是因为引用了库, 还有的原因是因为我觉得写得并不是很好.
1D Ising Model
注: 这个我不好说我到底有没有学过, 既然对这个名字完全没啥感觉, 那么就当作没有学过吧. 只是这个处理感觉非常熟悉. 怪.
- Ising 模型状态的描述:
(1 -1 -1 ...)使用这样一个列表来进行描述. - Ising 模型的能量:
\[E = - J ∑_{\left\langle i, j \right\rangle} S_i S_j - μ\sum h_j S_j\]
以防你和我一样热统没学得太好
我对 Ising 模型的理解是:- Ising 模型描述的是一堆磁矩在外场中随着不同温度变化的一个分布
- \(- μ ∑ h_j S_j\): 磁矩在外磁场中的能量, 其中 \(h_j\) 为第 \(j\) 个粒子受到的磁场
- \(- J ∑_{\left\langle i, j \right\rangle} S_i S_j\): 磁矩相互之间的作用, 这里仅考虑最临近的相互作用, 对于一维模型来说, 就是左右粒子, 对于二维模型来说, 就是上下左右.
- 边界条件
在这里仅从物理的描述上对能量进行计算, 并不涉及为了之后的仿真做计算量上的优化:
- 相互作用项:
(let ((J-ij (lambda (i j) ; 默认只有上下 (declare (ignore i j)) 1))) (defun 1-d-ising-set-J (func) (setf J-ij func)) (defun 1-d-ising-interaction-e (state) "E_interaction = - ∑ J_ij S_i S_j; i, j = nearest neighors" (let ((sum 0)) (loop for sj in (rest state) for j from 2 for si in state for i from 1 do (setf sum (+ sum (* (funcall J-ij i j) si sj)))) (* -1 sum))))
- 外场项:
(let ((field (lambda (n) ; 默认为和外场无关的恒磁场 (declare (ignore n)) 1)) (μ 1)) (defun 1-d-ising-set-μ (μ-value) (setf μ μ-value)) (defun 1-d-ising-set-field (func) (setf field func)) (defun 1-d-ising-field-e (state) "E_field = - μ ∑ hj sj" (let ((sum 0)) (loop for sj in state for j from 1 ; 从 1 开始对 j 进行标号 do (setf sum (+ sum (* (funcall field j) sj)))) (* -1 μ sum))))
- 总场
(defun 1-d-ising-e (state) (+ (1-d-ising-interaction-e state) (1-d-ising-field-e state)))
- 状态转移的生成: 随机翻转一个磁矩.
(defun 1-d-ising-gen (state) (let ((i (random (length state))) (new (copy-list state))) (setf (nth i new) (* -1 (nth i state))) new))
- 判断函数
(let ((kT 300)) (defun 1-d-ising-set-kT (kT-value) (setf kT kT-value)) (defun 1-d-ising-acc (state2 state1) (let ((dE (- (1-d-ising-e state2) (1-d-ising-e state1)))) (or (< dE 0) (< (random 1.0) (exp (- (/ dE kT))))))))
- 采样后的后处理
(注: 使用的问题来自 Exercise: One-dimensional Ising model, 但是不建议把那个网站当作学习参考, 当大纲估计挺好.)
- \(N = 20, T = 1.0\), 计算每一步的能量并估计稳定所需要的步数
(也就是之后仿真用的
burn-in参数).没时间优化代码了, 就这么看吧:
(let ((res-list '())) (loop for kT in kT-list do (progn (1-d-ising-set-kt kT) (let ((energy-hist '())) (sampling-hist (make-list 20 :initial-element -1) #'1-d-ising-gen #'1-d-ising-acc samples 0 (lambda (state) (setf energy-hist (cons (1-d-ising-e state) energy-hist)))) (push (list (format NIL "kT = ~a" kT) (reverse energy-hist)) res-list)))) (lists-plot output res-list))
能量 (纵坐标) 随仿真步数 (横坐标) 的变化:
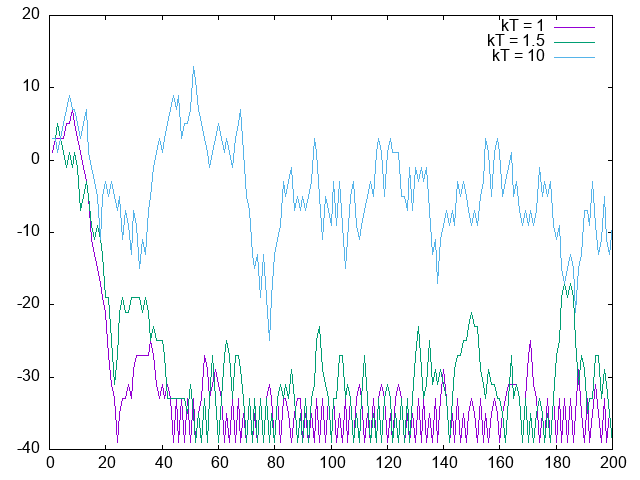
基本可以看到, 基本只要大约 50 步左右就稳定了. 但是随着温度的升高, 热运动占主导, 就变得比较不稳定. 而当温度进一步提高, 则会导致场的影响变弱.
绘图代码
(defun list-points-plot (output lst &key (title "")) "图片输出路径: `output', 输入点列表: `lst', 元素为 `(x . y)'." (eazy-gnuplot:with-plots (s :debug NIL) (eazy-gnuplot:gp-setup :terminal :png :output output) (eazy-gnuplot:plot (lambda () (loop for point in lst do (format s "~&~a ~a" (car point) (cdr point)))) :with '(line) :title title)) output) (defun lists-plot (output lists) "输出路径: `output', 绘制元素列表: `lists', 元素为: `(标题 (y 值))'" (eazy-gnuplot:with-plots (s :debug NIL) (eazy-gnuplot:gp-setup :terminal :png :output output) (loop for lst-desc in lists do (eazy-gnuplot:plot (lambda () (loop for elem in (second lst-desc) for i from 1 do (format s "~&~a ~a" i elem))) :with '(:lines) :title (first lst-desc)))) output)
- 不同温度下的平均能量和平均磁矩
(同上, 没时间写代码)
(let ((average-e '())) (loop for kt from 1 below 10 by 0.1 do (progn (1-d-ising-set-kt kt) (let ((energy-hist (make-histogram 500))) ; 500 bins (set-ranges-uniform energy-hist -50d0 50d0) ; hist from -50 to 50 (sampling-hist (make-list 20 :initial-element -1) #'1-d-ising-gen #'1-d-ising-acc 1000 50 (lambda (state) (increment energy-hist (coerce (1-d-ising-e state) 'double-float)))) (let ((sum 0)) (loop for i below 500 for e from -50 below 50 by (/ 100 500) do (setf sum (+ sum (* e (grid:aref energy-hist i))))) (push (cons kT (/ sum 500)) average-e))))) (list-points-plot output average-e :title "<E>"))
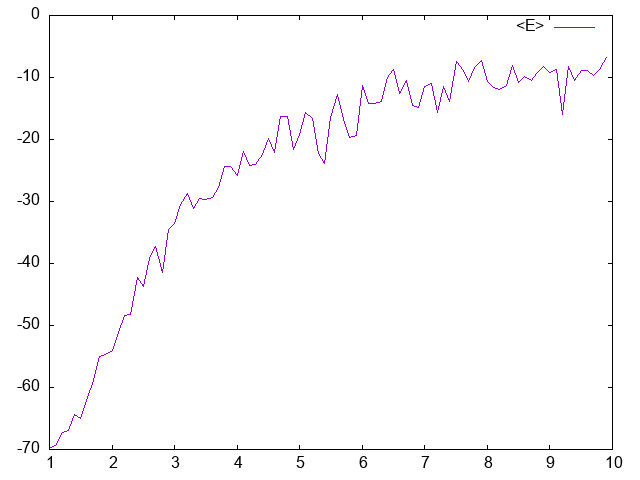
平均磁矩:
(真没时间写代码)
(let ((average-m '())) (loop for kt from 1 below 10 by 0.1 do (progn (1-d-ising-set-kt kt) (let ((m-hist (make-histogram 500))) ; 500 bins (set-ranges-uniform m-hist -25d0 25d0) ; hist from -50 to 50 (sampling-hist (make-list 20 :initial-element -1) #'1-d-ising-gen #'1-d-ising-acc 1000 50 (lambda (state) (increment m-hist (coerce (apply #'+ state) 'double-float)))) (let ((sum 0)) (loop for i below 500 for m from -25 below 25 by (/ 50 500) do (setf sum (+ sum (* m (grid:aref m-hist i))))) (push (cons kT (/ sum 500)) average-m))))) (list-points-plot output average-m :title "<M>"))
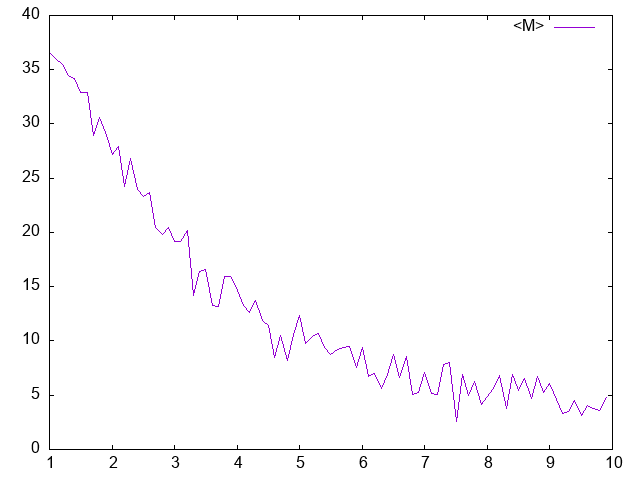
- \(N = 20, T = 1.0\), 计算每一步的能量并估计稳定所需要的步数
(也就是之后仿真用的
代码实在是太丑了
2D Ising Model
现在开始写了一点, 出来的结果狗屁不通. 决定重新开始写. 欸.
目标: (2-d-ising-sim (n m) kt samples :sample-step 100 :init 1 :plot (e m)).
- 初始化 2D Ising 模型:
;;; (at mat x y) -> (nth x (nth y mat)) (defmacro at (mat &rest pos) (if (null pos) mat `(nth ,(first pos) (at . (,mat . ,(rest pos)))))) (defun init-2-d-ising (n &optional (m n) (init 1)) "2D Ising model: nxm matrix, n is x size, m is y size. `init' can be fixed constant or symbol `random' or specific function. " (cond ((functionp init) (loop for j below m collect (loop for i below n collect (funcall init i j)))) ((numberp init) (loop for j below m collect (loop for i below n collect init))) (T (loop for j below m collect (loop for i below n collect (1- (* 2 (random 2))))))))
- 每次记录一个翻转位置
(i . j)而不是记录翻转后的整个模型. (其实 Lisp 应该传的是指针, 所以应该并不会减少传值开销, 只是为了之后计算能量的时候可以减少一些计算量而已). - 每次更新的时候, 需要根据模型刷新一个新的位置.
(defun make-2-d-ising-gen (model) "生成一个 gen 函数." (let ((m (length (first model))) (n (length model))) (lambda (pos) (declare (ignore pos)) (cons (random n) (random m)))))
- 对于已有的系统, 在翻转了一个元素之后计算能量改变的时候, 只需要计算临近前后的能量变化而不需要计算整个系统. (这样可以把计算速度大大提高)
- 每次判断的时候判断能量改变:
(defun make-2-d-ising-acc (model kT) "生成一个 acc 函数." (let ((n (length (first model))) (m (length model))) (lambda (pos2 pos1) (declare (ignore pos1)) (let* ((i (car pos2)) (j (cdr pos2)) (spin (at model i j)) (near (+ (at model (mod (1+ i) n) j) (at model i (mod (1+ j) m)) (at model (mod (1- i) n) j) (at model i (mod (1- j) m)))) (dE (* 2 spin near))) (or (< dE 0) (< (random 1.0) (exp (- (/ dE kT)))))))))
- 每次模拟后进行一个数据记录:
(defun make-store-function () "返回一个添加函数和读取函数." (let ((stored '())) (values (lambda (elem) (push elem stored)) (lambda () (reverse stored))))) (defun make-2-d-ising-yield (step store-fn store-place-fn) (let ((counter 0)) (lambda (pos) (setf counter (mod (1+ counter) step)) (if (eq counter 0) (funcall store-place-fn (mapcar (lambda (fn) (funcall fn pos)) store-fn)) (mapcar (lambda (fn) (funcall fn pos)) store-fn)))))
其中数据记录函数可以有:
- 能量
(defun 2-d-ising-e (model &optional (n (length (first model))) (m (length model))) (let ((energy 0.0)) (loop for j below m do (loop for i below n do (let ((spin (at model i j)) (near (+ (at model (mod (1+ i) n) j) (at model i (mod (1+ j) m)) (at model (mod (1- i) n) j) (at model i (mod (1- j) m))))) (setf energy (- energy (* spin near)))))) (/ energy 4))) (defun make-2-d-ising-energy-rec (model) "生成一个根据 dE 来计算模型能量的函数" (let ((n (length (first model))) (m (length model)) (energy (2-d-ising-e model))) (lambda (pos) (let* ((i (car pos)) (j (cdr pos)) (spin (at model i j)) (near (+ (at model (mod (1+ i) n) j) (at model i (mod (1+ j) m)) (at model (mod (1- i) n) j) (at model i (mod (1- j) m))))) (setf energy (* 2 spin near))))))
- 磁矩
(defun 2-d-ising-m (model) "计算系统的磁矩." (let ((m 0)) (loop for line in model do (setf m (+ m (apply #'+ line)))) m)) (defun make-2-d-ising-m-rec (model) (let ((mag-m (2-d-ising-m model))) (lambda (pos) (let ((spin (at model (car pos) (cdr pos)))) (setf mag-m (+ mag-m (* 2 spin)))))))
- 能量
- 于是一个模拟过程如下:
(defun 2-d-ising-sim (size kT samples &key (sample-step 1) (burn-in 0) (init 1)) (let ((model (init-2-d-ising (car size) (cdr size) init))) (multiple-value-bind (write-rec read-rec) (make-store-function) (sampling-hist '(0 . 0) (make-2-d-ising-gen model) (make-2-d-ising-acc model kT) samples burn-in (make-2-d-ising-yield sample-step (list (make-2-d-ising-energy-rec model) (make-2-d-ising-m-rec model)) write-rec)) (funcall read-rec))))
- 一次可能的模拟:
如何更强一些?
- 随机数算法: 如何让随机数产生得更加合理?
- 代码的更进一步的优化.
- 比如使用 vector (array) 来代替 list 作为向量表示, 进一步提高计算速度 (虽然不清楚会快多少).
- 计算能量的代码通过 Hash 对代码计算值进行缓存处理, 提高计算速度. (这个我在 On Lisp 里面看到过, 但是具体怎么做已经忘光了).
- 使用多线程计算, 不过该怎样把这个一条 Markov 链的计算变成多线程, 我觉得可能可以把长度减少, 然后同时并行运行多个计算链.
- 物理, 我要学更多的物理!
- 自动判断是否在稳定状态: 通过接受率和拒取率来判断, 具体怎么做还没看.
Others
那么就让这篇文章成为一个简单的小笔记吧.
一些问题的无聊解答
- 这 TMD 什么编程语言?
Lisp, Common Lisp, Common Lisp via SBCL distribution.
- 为什么用 Lisp 而不用 XXX?
因为好玩? 且 C 不太会用, Python 很少用, Ruby 太慢, 其他语言不熟.
- 那么如何学 Lisp 呢?
实际上我觉得计算逻辑部分的代码非常好懂, 如果知道要算法算的是啥, 那么这个 Lisp 代码我觉得就是没学过的人随便看看也能看懂吧.
- 等一下, 这个和退火算法有什么关系?
好问题, 虽然不一定是好问题, 但是我觉得是个好问题.
退火算法 (具体大概就是一个加上一个随时间逐渐确定的随机游走的贪心算法来找最大值), 在这里用物理的角度就是: 外场一开始的影响在温度的影响下比较小, 所以在 Markov 链游走的时候, 会尽可能地去历遍更多可能的状态; 而随着温度的降低, 外场开始起主导作用, 这个时候就会去势场最低, 也就是极值点.
之所以不简单使用梯度下降, 是因为梯度下降是局域贪心算法, 不一定找到的就是全局极值. 而退火算法因为引入了随机游走, 有一定概率能够漂移出局部极值的坑.
所以可以将这样的算法应用到极值问题中, 从而可以对多维极值优化进行求解.
欸, 那么这是否就是一个当代显学人工智能需要操心的问题了呢?
看, 这就是学统计物理常用的话术: 学会统计物理, 你就会机器学习了.
然而并没有.