回转微重力罐
小时候, 我想当太空人
爸爸给了我最爱吃的大嘴巴子

啊, 还是不整这些烂活了. 让我们抛开大嘴巴子这个梗… 不知道在座的是否小时候被自己大一些的孩子忽悠过: 如果被打了头, 就会变笨 – 但是不用担心, 再打一下就可以变回来了…
合力抵消与失重
显然, 这种 “合力抵消” 的哄小孩的鬼话和仗着耶稣说的 “有人打你的右脸, 连左脸也转过来由他打” 的 “名言” 来捉弄比自己小的孩子的诡计, 也只能骗骗那些纯真无邪的小笨蛋以及相信着交感巫术的一些人们.
所以, 小孩子才要两个巴掌, 大孩子都知道, 两个力的合力为零, 当然是这两个力等大反向 (注: 又因为现实中少有刚体, 严谨一些的同学可能还会加入作用力通过转轴这样的限制条件. )
那么, 还是回到太空人的幻想中去, 成为太空人的美妙幻想之一便是 无重力环境的失重感: 漫步繁星之中, 感到逃脱引力的自由.
然而, 事实上, 除非我们远远地逃离中心天体的引力 ($lim_{r → ∞} \frac{G M m}{r^{2}} → 0$), 否则我们仍然受到引力的拖曳. 但是两个巴掌的故事告诉我们, 只要有另外一个力能够和引力等大反向, 于是我们所受到的合力便可视为零, 于是就产生了一种 “不受任何力” 的时空错觉.
在故事中的这个另外的一个力, 比如在太空站中, 即绕转地球的运动中的 “离心力”.
在地面上的微重力故事
然而, 想要满足使离心力与引力抵消:
$$\frac{G M m}{r^2} = \frac{m v^2}{r} ⇒ v = \sqrt{\frac{G M}{r}}$$
我们需要至少达到约 $7.9 km/s$ 的第一宇宙速度 ($R ≈ 6370km$), 而这则需要巨大的能量 – 哦, 这该死的生命所承受之重. 而若我们轻盈微小宛若小小一细胞, 渺渺一微生物, 想必一定能够轻松带上天吧.
你说的对, 尽管科学家们已经实现了许许多多的空间站培养微生物的实验, 但是我们并不能做到轻松地将所有的微生物培养的成套装置一起打包上天. 于是一个朴素的想法便是 如何在地面上去模拟一个微重力的环境呢?
Human Fall Flat自由落体:这是飞一般的感觉~

一个朴素的想法就是, 既然在自由落体的时候, 可以等效为失重状态; 那么如果造一个高塔, 把被试验的对象从上面丢下来, 不就是一段失重的体验了么.
显然, 这可能不是一个非常好的点子. 因为倘若我们想要增加失重的时间, 便会发现, 我们需要的下落高度便会随时间平方增加: \(l = \frac{1}{2} g t^2\). 哪怕是世界记录的跳伞 (2014, Alan Eustace, 41.419km), 也仅能维持约 \(\sqrt{\frac{2 × 41.419 \mathrm{km}}{9.8 \mathrm{m ⋅ s^{-2}}}} ≈ 1 \mathrm{min} 31 \mathrm{s}\) (当然, 事实是 4 分 36 秒, 因为肯定还要用降落伞啊, 怎么可能是完全自由落体).
感受不到法模拟太空失重的感觉眼见不一定为实, 体感亦是如此.

尽管没法真的抵消重力, 但是人们发现, 在一定情况下, 生物可以表现出失重的感觉. 譬如将人泡在水中, 或是长时间卧床 (头低位 \(6^{ˆ}\) ); 或是将小鼠低位尾吊…
这样的 “差不多得了” 的感觉, 除了在上面的受力形式上做文章, 还能够在时间上做文章: 使得受到的平均力 \(\left< \boldsymbol{F} \right>_{T} → 0\) 倘若 \(T\) 在一个生物感觉不到的阀值内 – 即乘生物不注意, 使得力变得太快了而看起来没有变化.
是不是有一种两个时间平均抵消的巴掌就等价于没有巴掌的感觉? (bushi)

回转仪
使得平均力 \(\left< \boldsymbol{F} \right> → 0\) 的思路的一个应用即是回转仪:
关于回转仪, 倘若在座的各位曾经去过类似于天文馆, 一定见过那种将人绑在椅子上放在一个滑环里转悠的体验装置吧. 或者, 哪怕没吃过猪肉, 总见过猪跑吧… 在刷小视频时, 一定见过不少类似的东西吧:

(注: 图片来源 (手工耿) 为了体验下在太空里那种失重旋转的感觉自己做了辆失重离心车. )
啊, 回转仪差不多就是这么个感觉: (一个比较抽象的图, 之后会有更加具体的图. )
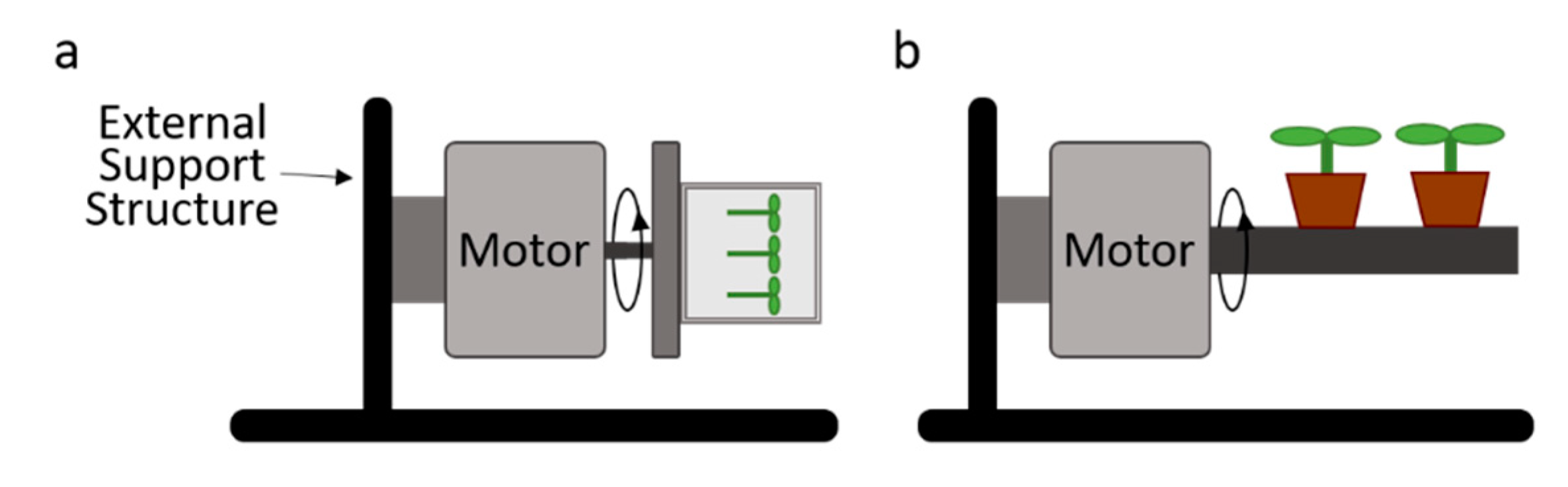
(注: 图片来源于 Advantages and Limitations of Current Microgravity Platforms for Space Biology Research (Figure. 1), 其中做了裁剪选择了 a, b 部分. 用于描述 2D 的回转仪. )
也许你第一印象是: 回转仪是通过高速旋转产生的离心力来抵消重力, 达到失重的状态. 嘻嘻嘻, 并不是这样的呢. 因为离心力的方向始终是径向向外, 所以在最低点处受到的等效重力 \(g_{\mathrm{b}} = g_{ω} + g_0\), 而在最高点的等效重力为 \(g_{\mathrm{t}} = - g_{ω} + g_0\) (向下为正).
于是在最低点处, 物体出于超重状态, 在高速旋转时, 如此大的等效重力会带来不可承受的压力. 这可不是什么好事情.
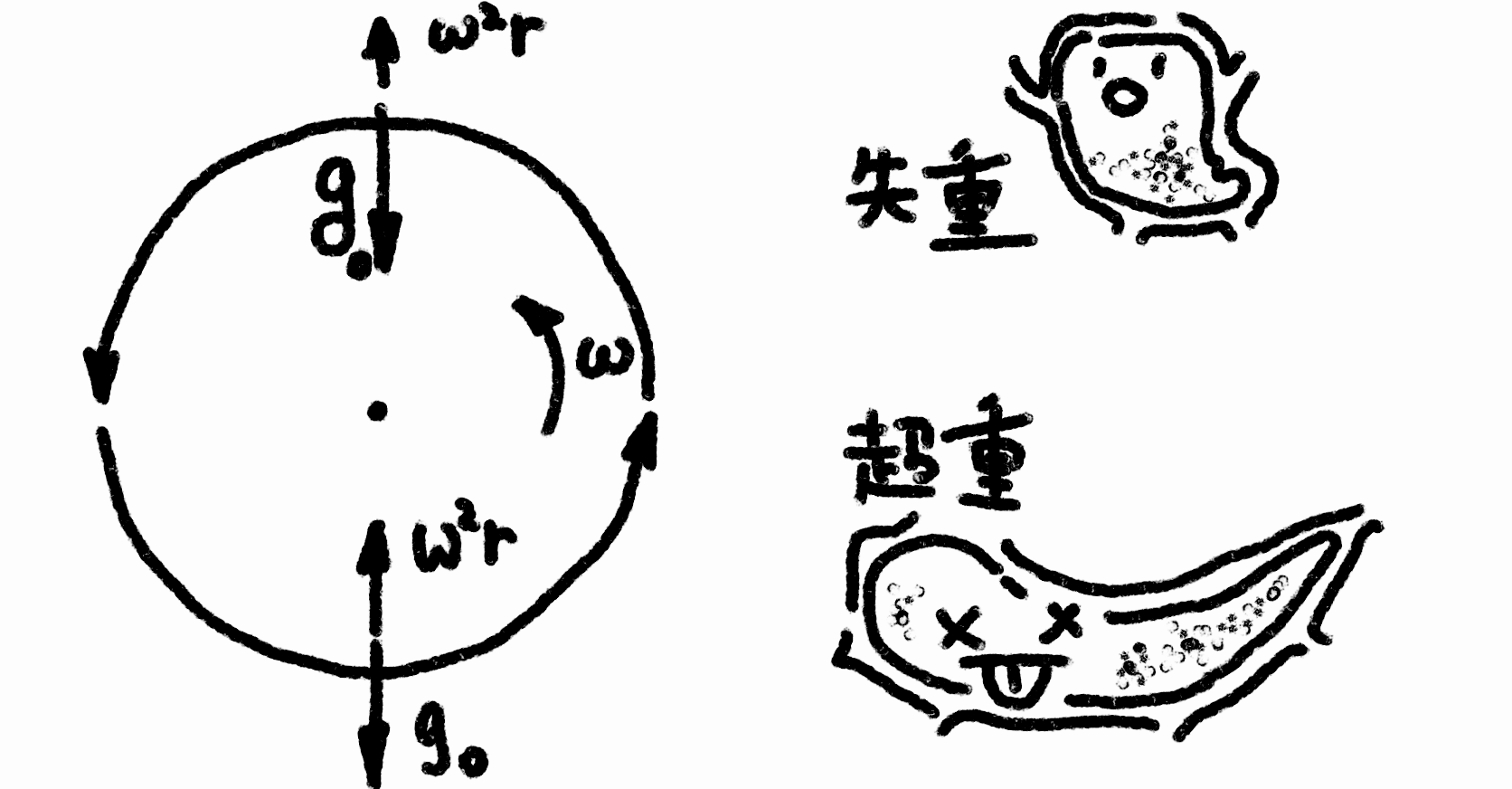
而正如前文所说的, 回转仪的思路是使得平均重力为零而非抵消重力. 所以我们不妨换位思考, 站在被绑在转轴上的物体的角度: 于是不难发现, 在旋转的过程中, 感受到的重力的方向在慢慢地发生着变化. 在上图的 2D 回转仪 (单轴回转仪) 的例子中, 倘若令转轴为 \(z\) 轴, 我们可以简单地给出重力的一个表达式:
\[\boldsymbol{g} = cos (ω t + \varphi) g_0 \boldsymbol{e}_x + sin (ω t + \varphi) g_0 \boldsymbol{e}_y\]
于是在对一个时间周期 \(T = \frac{2 π}{ω}\) 进行积分, 可以得到:
\[\left< \boldsymbol{g} \right> = ∫_{k T}^{(k + 1) T} \boldsymbol{g} \mathrm{d}t = \boldsymbol{0}\]
这便是数学上的回转仪的原理了. 而从直观的理解上看, 这便和两个方向相反的巴掌在时间上 “平均” 变成没有巴掌一样了么 (bushi).
倘若我们固定重力矢量的起点为坐标原点, 那么其终点所落的位置便如下图所示:
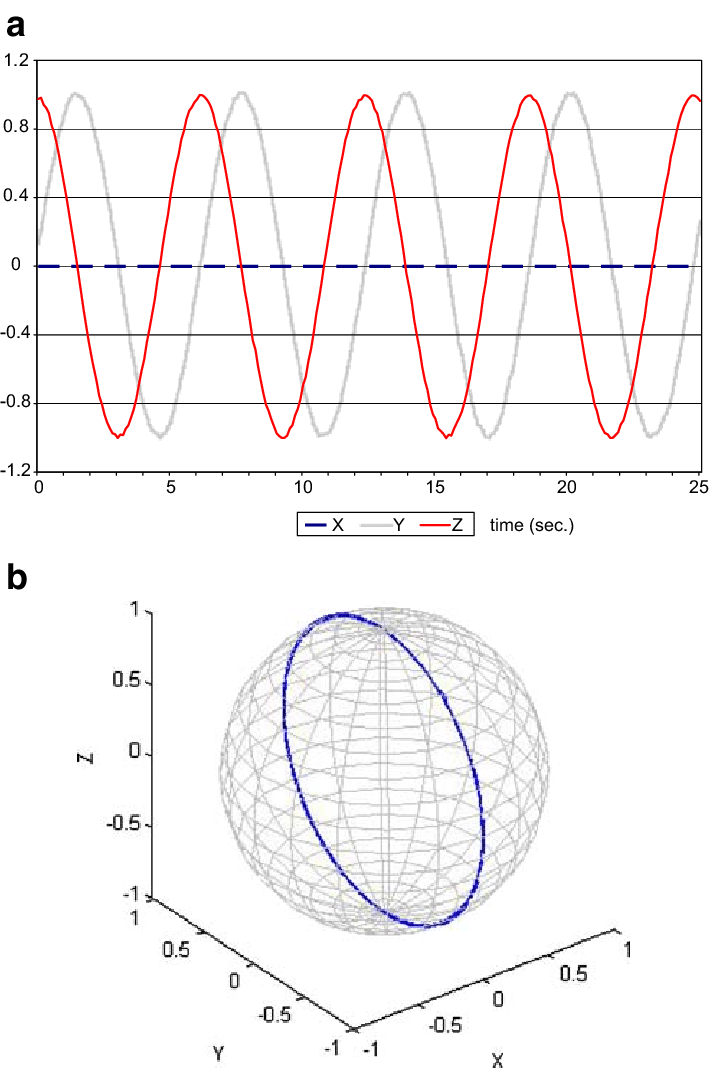
(注: 图片来源 Technology and Developments for the Random Positioning Machine, RPM (Figure 3), 其中红色的轨迹为 2D 单轴回转仪的重力矢量路径. )
我们会看到在单轴回转仪中的运动轨迹是单一的, 虽然能够 “抵消” 重力, 但是并不能像科幻小说中描绘的那样: 完美地控制重力, 比如控制重力的大小之类的.
但是倘若我们追求 “多即是好” 的原则, 再加入一个旋转轴, 此时便能构造得到一个二轴回转仪:
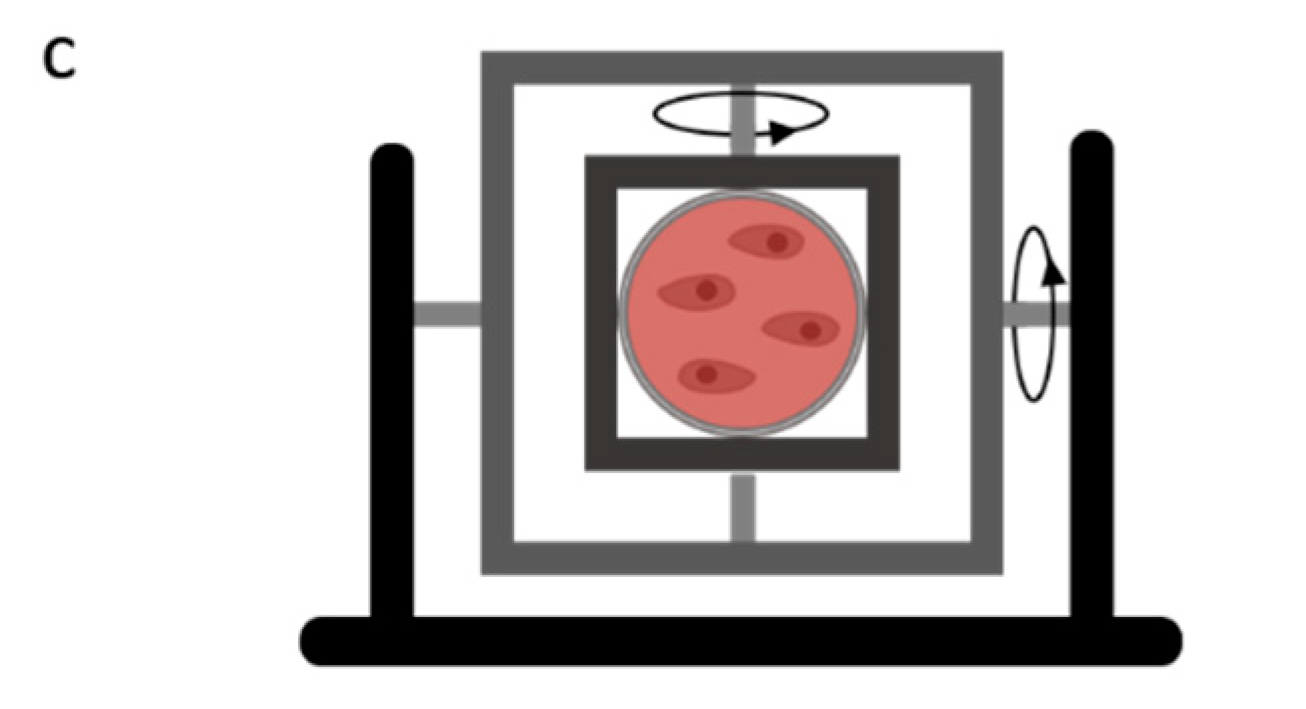
(注: 图片来源于 Advantages and Limitations of Current Microgravity Platforms for Space Biology Research (Figure. 1), 其中做了裁剪选择了 c 部分. 用于描述 2 轴的回转仪. )
而这个时候, 结果便不同了, 通过配置每个轴的转动速度之比, 可以得到不同的结果:
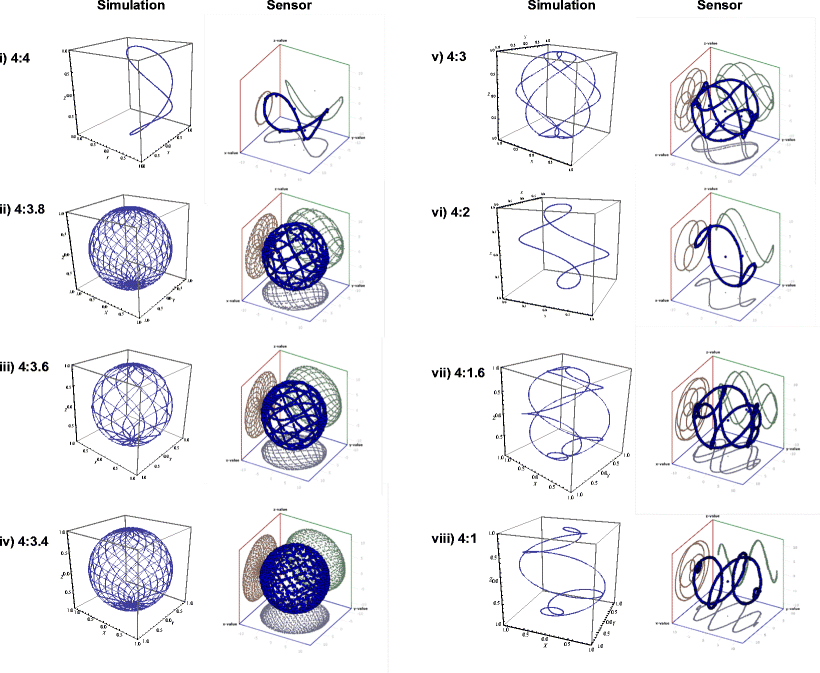
以及重力在竖直方向的投影的值:
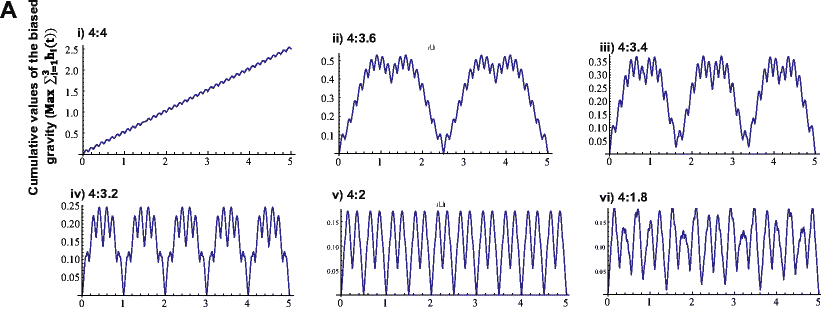
可以看到, 平均重力在不同转速比例下是略有不同的. 通过设置合理的转速比, 可以模拟任意大小的重力加速度.
而另外一种思路, 即让两个轴的转动随机, 于是便可以得到 Random Position Machine (机翻: 随机定位机):

(注: 图片来源 ESA: Random Positioning Machine)
通过这样的方式进行微重力模拟, 可以进一步消除在匀速转动中由于离心力带来的系统误差.
这就是微重力回转仪.
所以下一次再有听到小时候我要当太空人, 请记得给两个在时间上平均为零的巴掌之后再用这篇文章来说服他们吧 (bushi)